Лекция № 10

Числовые ряды. Критерий сходимости Коши.

Свойства сходящихся рядов

Пусть дана бесконечная последовательность чисел .

Определение 1. Бесконечная сумма называется рядом. Числа – члены ряда.

Ряд задан, если для любого известно правило, ставящее в соответствие номеру член ряда.

Ряд может быть задан:

1. формулой – го члена (например, ),

2. рекуррентным соотношением (например, , ).

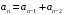Составим суммы . Величины называются частичными суммами ряда.

Определение 2. Если существует предел последовательности частичных сумм , то говорят, что сходится бесконечный ряд и его сумма равна _.

Если же не существует, либо он бесконечен, то говорят, что ряд расходится.

Ряд может расходиться в двух случаях:

1. ,

2. последовательность не имеет предела.

Можно кратко переформулировать данное выше определение: Ряд сходится тогда и только тогда, когда существует предел его частичных сумм.

Пример 1. Рассмотрим геометрическую прогрессию 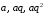,, . Из алгебры известно:

.

Если , то и , т.е. ряд сходится.

Если то и ряд расходится.

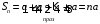Если , то ряд имеет вид и .

Если , то . Такая последовательность не имеет предела, следовательно, ряд расходится.

Рассмотрим сходящийся ряд 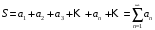. Разность называется – ым остатком ряда (тоже сумма ряда).

Утверждение 1. Ряд сходится тогда и только тогда, когда для любого остаток – сходится.

Итак, исследование сходимости ряда и исследование сходимости любого его остатка – эквивалентные задачи. Это означает, что при изучении сходимости достаточно рассматривать лишь члены ряда, начиная с некоторого номера. Это не влияет на сходимость. Изменится лишь сумма ряда.

Свойства сходящихся рядов.

Пусть , , и - постоянная величина. Тогда:

1. ,

2. ,

3. Если ряд сходится, то сходятся так же и другие ряды, полученные из исходного ряда добавлением, удалением или перестановкой конечного числа членов. (Сумма ряда может измениться).

Критерий Больцано-Коши сходимости ряда.

Исходим из критерия Больцано-Коши для сходимости последовательности частичных сумм .

(Ряд сходится) .

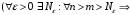
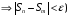
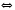
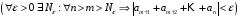Необходимый признак сходимости ряда.

Теорема 1. Если ряд сходится, то .

Доказательство. . Ряд сходится . Тогда .

Важный пример, показывающий, что необходимый признак сходимости отнюдь не является достаточным.

Пример 8.2. Ряд называется гармоническим. Очевидно, т.е. общий член стремится к 0. Покажем, что этот ряд расходится. Используем критерий Больцано-Коши. Следует доказать, что

.

В качестве выберем число . Берем любое и любое . Пусть . Тогда

.

Утверждение 2. (Достаточный признак расходимости ряда) Если 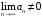, то ряд – расходящийся.

Ряды с неотрицательными членами. Теоремы сравнения.

Признаки Даламбера, Коши, Гаусса

Если известно, что все члены ряда имеют, начиная с некоторого номера, постоянный знак, то исследовать его сходимость проще, чем в общем случае. Это связано с тем, что у знакопостоянных рядов последовательность частичных сумм монотонна. Для определенности будем считать, что все . Тогда частичные суммы ряда образуют монотонно возрастающую последовательность.

Теорема 2. (Критерий сходимости рядов с неотрицательными членами). Для сходимости ряда где необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена.

Доказательство.

Необходимость. Пусть. Тогда .

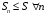Достаточность. Пусть . Поскольку , последовательность возрастает и, по условию, ограничена. Следовательно, по теореме Вейерштрасса (см. 1-ый семестр), она имеет предел, то есть ряд сходится.

Простые следствия из этого критерия – очень полезные теоремы сравнения.

Теорема 3. (Допредельный признак сравнения) Пусть выполняется неравенство и пусть ряд – сходится. Тогда сходится ряд .

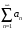Доказательство. Очевидны неравенства . По условию 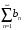– сходится. Значит, по приведенному выше критерию, . Но тогда и и, значит, ряд - сходится.

Примечание 1. Эта теорема может быть сформулирована и так: Пусть выполняется неравенство 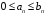и пусть ряд – расходится. Тогда рассходится ряд . Действительно, если бы этот ряд сходился, то по теореме сравнения должен был бы сходиться и ряд .

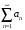Примечание 2. Теорема сравнения справедлива и в случае, когда неравенство выполняется, начиная с некоторого номера .

Теорема 4. (Предельный признак сравнения). Пусть и . Тогда ряды и сходятся или расходятся одновременно. (Т.е. не может быть так, что один из них сходится, а другой расходится).

Доказательство. . Выберем . Тогда (т.к. ) при .

Если ряд – сходится, то сходится и ряд (по примечанию 2 к допредельной теореме сравнения). Тогда и ряд – сходится.

Если ряд – сходится, то сходится и ряд 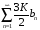и, следовательно, сходится ряд .

Теорема доказана.

Пример .3. Ряд сходится, т.к.

при и ряд 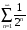– сходится.

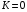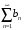Примечание 3. Если , то, начиная с некоторого номера , имеем и из сходимости ряда следует сходимость ряда 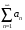, а из расходимости ряда следует расходимость ряда . Аналогично рассматривается случай .

6