
Индивидуальные контрольные задания по молекулярной физике Вариант 1
Модуль 1
1.Исходя из биномиального распределения Р(m,)доказать, что наиболее вероятным является состояние газа с равномерным распределением частиц по двум половинам объема:m=n/2, гдеn– число частиц во всем объемеV = 2. Использовать формулу Стирлинга.
2. Электроны в полупроводниках, сталкиваясь
с некоторыми атомами, так называемыми
локальными центрами, могут быть ими
захвачены. Сечение захвата σ зависит
от кинетической энергии электрона Е гдеa– константа.
Определить зависимость от температуры
среднего времени жизни электрона до
захвата
гдеa– константа.
Определить зависимость от температуры
среднего времени жизни электрона до
захвата .
Концентрация локальных центров захватаnцизвестна.
Считать, что для электронов в полупроводниках
справедлива статистика Максвелла.
.
Концентрация локальных центров захватаnцизвестна.
Считать, что для электронов в полупроводниках
справедлива статистика Максвелла.
3. Через какое время tнасос Ленгмюра откачает двухлитровый
баллон с воздухом от давления мм
рт. ст. до
мм
рт. ст. до мм рт. ст.,
если баллон соединён с насосом трубкой
длиноюl= 25 см
и диаметраD= 7 мм?
Скорость откачки насосаK= 1000
см3/с. Температура воздухаt= 18°C.
мм рт. ст.,
если баллон соединён с насосом трубкой
длиноюl= 25 см
и диаметраD= 7 мм?
Скорость откачки насосаK= 1000
см3/с. Температура воздухаt= 18°C.
Модуль 2
4.
Воду, находящуюся при 0 ºCи давленииР= 100 атм,
расширяют адиабатически и квазистатически
до атмосферного давления. Найти изменение
температуры воды в этом процессе, если
коэффициент объемного расширения воды
в этих условиях отрицателен и равен ºС-1.
ºС-1.
5. Найти уравнение адиабаты для газа, уравнение состояния которого дается в виде
P = P0(1 +αT−βV),
где постоянные ,иР0известны. Считать, что молярная теплоемкость газасvне зависит от температуры.
6. Тепловая машина с идеальным газом в качестве рабочего вещества совершает обратимый цикл, состоящий из изохоры, адиабаты и изотермы. Рассчитать количества тепла, получаемые рабочим веществом на каждом этапе цикла. Найти к. п. д. машины как функцию максимальной и минимальной температур, достигаемых газом в этом цикле.
7. Один моль Н2О охлаждается от температурыt1=25Cдоt2=0Cи замерзает. Всё тепло, полученное охлаждающей машиной, работающей с максимальной теоретически допустимой эффективностью, передаётся другому молюH2Oприt1=25C, в результате чего его температура повышается до 100С. Сколько молей Н2О переходит в пар при 100С? Какую работу должен произвести рефрижератор? Теплота испаренияqпри 100С равна
40,9 кДж / моль. Теплота плавления льда при 0С равна 6 кДж / моль.
Модуль 3
8.
Записать
уравнение реального газа типа Дитеричи
в приведённых переменных:
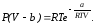
9. Один конец стержня поддерживается при температуре Т1, а другой – при температуре Т2. Сам стержень состоит из двух частей, длины которых l1 и l2, а коэффициенты теплопроводности 1 и 2. Найти температуру поверхности соприкосновения частей стержня.
10. Рассматривая удельную теплоту
испарения qкак работу, затрачиваемую
на преодоление внутреннего давленияPi,
найти зависимость междуPi,qи плотностью жидкости .
Считать, что жидкость подчиняется
уравнению Ван-дер-Ваальса.
.
Считать, что жидкость подчиняется
уравнению Ван-дер-Ваальса.
Вариант 2
Модуль 1
1.Допустим, что все молекулы воды в стакане как-то отмечены. После этого вода была вылита в водопроводный сток. По прошествии длительного времени вылитая вода равномерно перемешается со всей водой, имеющейся на Земле. Какое количество отмеченных молекул окажется в стакане, если его вновь наполнить водопроводной водой?
2.
Определить скорость конденсации паров
воды в комнате на холодном окне, если
предположить, что происходит захват
только тех молекул, которые налетают
на поверхность стекла с составляющей
энергии
 .
Координатная осьх
перпендикулярна поверхности стекла.
Процессы теплопроводности и конвекции
воздуха у окна не рассматривать.
.
Координатная осьх
перпендикулярна поверхности стекла.
Процессы теплопроводности и конвекции
воздуха у окна не рассматривать.
3.
В тонкостенный сферический баллон
массы м = 1 кг нагнетается азот
при температуре T = 300 К.
Найти максимальное количество азота,
которое можно поместить в сосуд, если
допустимое напряжение в стенках баллона
 = 50 Н
/ мм2.
Плотность стали
= 50 Н
/ мм2.
Плотность стали
 7,8 г/см3.
7,8 г/см3.
Модуль 2
4. Колесо паровоза имеет радиус r0= 1 м
приt0= 0ºC.
Определить разницу в числах оборотов
колеса летом при температуреt1= 25º С и зимой при температуреt1= −25º С на пути пробега паровозаl= 100 км. Коэффициент линейного
расширения металла колеса 0,000012º
С.
0,000012º
С.
5. Основной причиной понижения температуры с высотой в атмосфере является адиабатическое расширение восходящих потоков воздуха. Используя уравнение адиабаты идеального газа, найти изменение температуры с высотой.
6. Тепловая машина Карно используется в качестве холодильной машины для поддержания температуры некоторого резервуара при температуре t2 = –3 °С. Температура окружающего воздуха t1 = 27 °С. Какая механическая работа требуется для выполнения одного цикла машины, если при этом от оболочки резервуара отводится Q2 = 900 кал тепла?
7. Идеальный газ с показателем адиабаты совершает процесс по законуР= Р0−V, гдеР0и− положительные постоянные. При каком значении объемаVmэнтропия газа окажется максимальной.
Модуль 3
8. Найти уравнение политропы для газа Ван-дер-Ваальса, считая, что его теплоемкость Сvне зависит от температуры.
9. Постоянный электрический ток течёт по проводу, радиус которого Rи теплопроводность χ. В единице объёма провода выделяется тепловая мощностьw. Найти распределение температуры в проводе, если установившаяся температура на его поверхности равнаТ0.
10. Найти удельную теплоту испарения
бензола qиспвблизи его тройной точки, если известно,
что при этих условия его удельная теплота
плавленияqпл= 30,2 кал/г,
температура тройной точки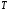 = 279 К,
равновесное давление пара в тройной
точкеР= 36 мм рт. ст. и
для кривой возгонки в той же точкеdP/dT= 2,43 мм рт. ст. / К.
Считать пар бензола идеальным газом.
= 279 К,
равновесное давление пара в тройной
точкеР= 36 мм рт. ст. и
для кривой возгонки в той же точкеdP/dT= 2,43 мм рт. ст. / К.
Считать пар бензола идеальным газом.
