Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Институт инженерной физики и радиоэлектроники СФУ

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Лекция 1

.doc

Скачиваний:

Добавлен:

09.06.2015

Размер:

625.66 Кб

Скачать

☆

Лекция № 15.

Определенный интеграл

Пусть на отрезке задана функция . Разобьем отрезок точками на элементарных отрезков длины . В каждом из этих отрезков возьмем произвольную точку и составим сумму , называемую интегральной суммой (Римана) для функции на отрезке .

Определение 37.1. Пусть предел последовательности интегральных сумм при стремлении к нулю существует, конечен и не зависит ни от способа разбиения отрезка , ни от выбора точек . Этот предел называется определенным интегралом от функции на отрезке и обозначается

(1)

При этом число называется нижним пределом, число – его верхним пределом; функция – подынтегральной функцией, выражение – подынтегральным выражением, а задача о нахождении – интегрированием функции на отрезке .

Все непрерывные на отрезке функции интегрируемы на этом отрезке. Интегрируемыми будут и ограниченные функции, имеющие на конечное число точек разрыва.

Свойства определенного интеграла

1. Определённый интеграл – это число! Его значение зависит только от вида функции и пределов интегрирования, но не от переменной интегрирования, которую можно обозначать любой буквой:

Интеграл был введен в предположении, что . Обобщим понятие определенного интеграла на случай, когда и .

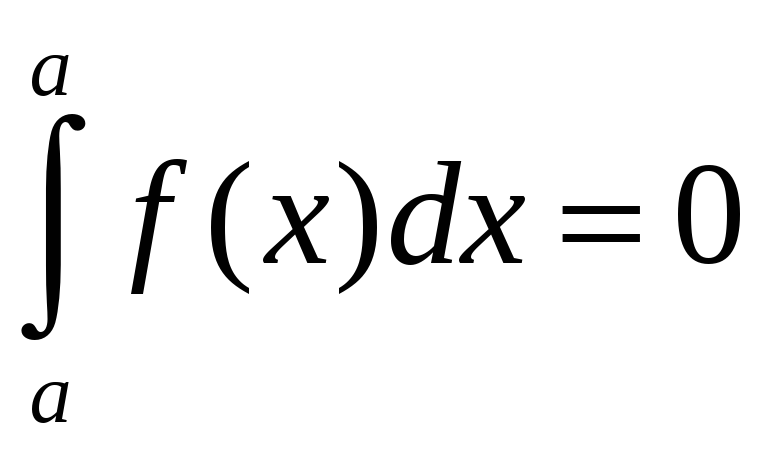2. . 3.

Рассмотрим свойства определённого интеграла, которые имеют аналоги в случае интеграла неопределённого.

4. Если , то .

5. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций: .

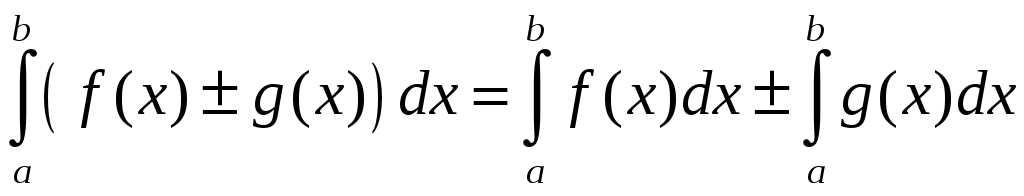Перейдем теперь к свойствам определённого интеграла, которые не имеют аналогов в случае неопределённого интеграла.

6. Если отрезок интегрирования разбит на части, то интеграл на всём отрезке равен сумме интегралов для каждой из возникших частей, т.е. при любых , , .

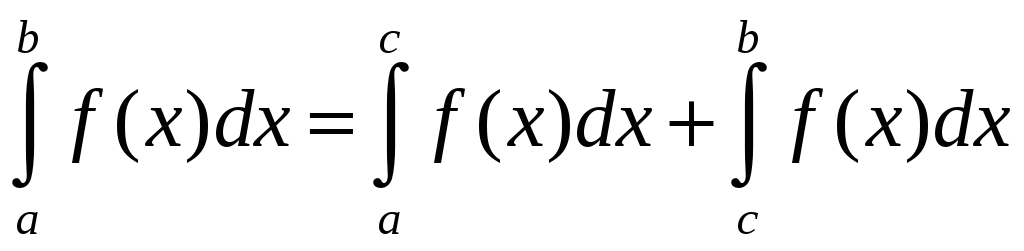7. Если на отрезке , то .

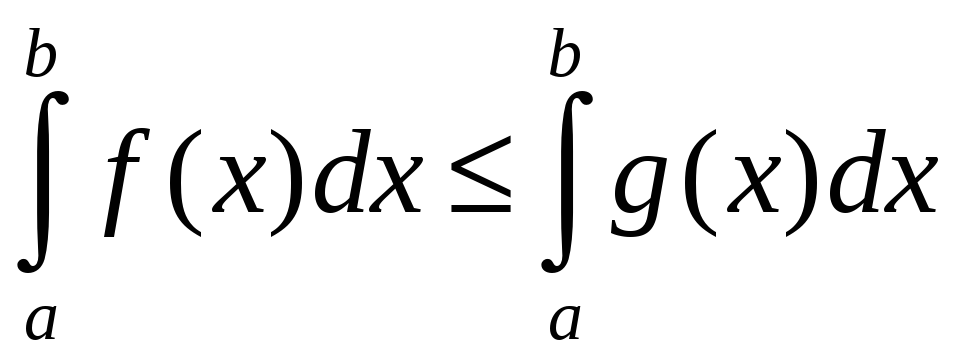8. Пусть на отрезке , где , . Тогда

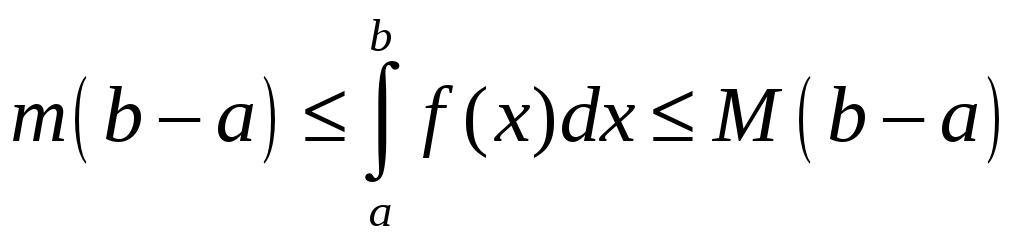9. Теорема о среднем. Если функция непрерывна на отрезке , то найдется такое число , что

10. Если функция интегрируема на отрезке , то функция также интегрируема на отрезке и имеет место неравенство

Геометрический смысл определенного интеграла

Понятие определенного интеграла введено таким образом, что в случае, когда функция неотрицательна на отрезке , где , численно равен площади под кривой на .

Учитывая сказанное, мы можем указать значения некоторых интегралов, используя известные планиметрические формулы для площадей плоских фигур. Например,

, , и т.д.

(Первый из интегралов – площадь квадрата со стороной единичной длины; второй – площадь прямоугольного треугольника, оба катета которого единичной длины; третий – площадь четверти круга единичного радиуса.)

Определенный интеграл как функция верхнего предела

Ранее, строя новые функции из известных, мы использовали четыре арифметических действия и суперпозицию функций. Сейчас мы рассмотрим принципиально иной способ построения новых функций из известных.

Если интегрируема на отрезке , то, очевидно, она интегрируема также на любом отрезке , вложенном в .

Положим по определению

где , а функция называется интегралом с переменным верхним пределом.

Пусть на отрезке . Тогда значение функции в точке равно площади под кривой на отрезке .

Это позволяет по новому взглянуть на некоторые известные функцию Например, , где , поэтому значение функции в точке численно равно площади под гиперболой на отрезке .

Рассмотрим теперь свойства функции .

Теорема 1. Пусть функция непрерывна на отрезке . Тогда в каждой точке отрезка производная функции по переменному верхнему пределу равна подынтегральной функции , т.е.

. (2)

Доказательство.

Покажем, что функция

(3)

является первообразной функции .

Согласно определению производной,

Применяя теорему о среднем к промежутку , представим интеграл в числителе в виде , где и при .

Следовательно, .

Теорема 2. Если функция непрерывна на отрезке , то функция также непрерывна на .

Вычисление определенного интеграла возможно с применением первообразной для функции по формуле Ньютона-Лейбница.

Теорема 3. Если функция непрерывна на отрезке и – первообразная функции , то

. (4)

Формула (4) называется формулой Ньютона–Лейбница.

Доказательство.

Возвратимся к уравнению (3). Полагая , находим значение постоянной :

Полагая в этом же уравнении , получаем:

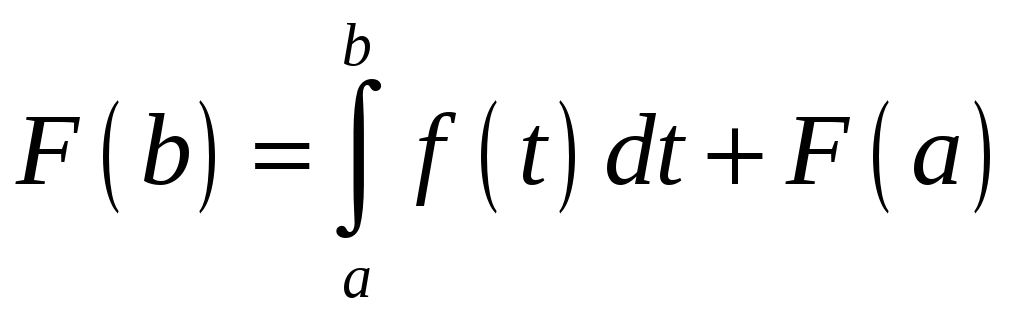
Нахождение определённых интегралов с использованием формулы (4) осуществляется в два шага: на первом шаге находят первообразную для подынтегральной функции ; на втором – применяется собственно формула (3) – находится приращение первообразной, равное искомому интегралу. Введем обозначение для приращения первообразной

Все методы, применяемые при вычислении первообразной, переносятся на вычисление определенного интеграла.

Теорема 4. (замена переменной в определённом интеграле). Если выполнены условия:

1) функция непрерывна на отрезке ;

2) отрезок является множеством значений функции , определенной на отрезке и имеющей на нем непрерывную производную;

3) и , то справедлива формула

Пример 1. Вычислить .

Решение. Положим . Тогда и .

Если , то , и если , то . Следовательно,

Формула замены переменной для определённого интеграла даже удобнее, чем для неопределённого. Нам не нужно возвращаться к исходным переменным, а вместо этого нужно поменять пределы интегрирования.

Рассмотрим, как выполняется интегрирование по частям в определённом интеграле.

Теорема 5. Если функции и имеют непрерывные производные на отрезке , то справедлива формула

Пример 2. Вычислить .

Решение.

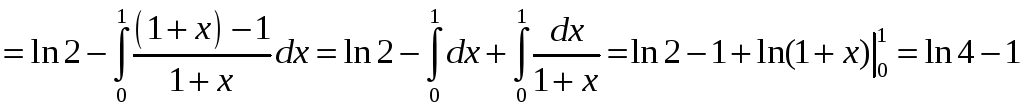Геометрические приложения определенного интеграла

Вычисление площадей плоских фигур. Если непрерывная кривая задана в прямоугольных координатах уравнением , где на отрезке , то площадь криволинейной трапеции, ограниченной этой кривой, двумя вертикалями ; и отрезком оси абсцисс , вычисляется по формуле

Пример 3. Вычислить площадь, ограниченную параболой , прямыми , и осью абсцисс.

Решение.

Пример 4. Вычислить площадь, ограниченную кривой и осью ординат.

Решение. Здесь изменены роли осей координат, поэтому искомая площадь будет выражаться интегралом

В общем случае, если площадь ограничена двумя непрерывными кривыми ; и двумя вертикалями ; , где , для вычисления площади фигуры имеем формулу

Пример 5. Вычислить площадь , заключенную между кривыми и .

Решение. Найдем точки пересечения кривых: , , . На отрезке . Значит,

Параметрическое задание верхней границы криволинейной трапеции

При вычислении площади криволинейной трапеции, в случае когда верхняя граница задана параметрическими уравнениями

в формуле надо сделать замену переменной, положив , , тогда получим , где a и b - значения параметра , соответствующие значениям и , т. е. ; .

Пример 6. Найти площадь фигуры, ограниченной одной аркой циклоиды и осью .

Решение. Искомая площадь

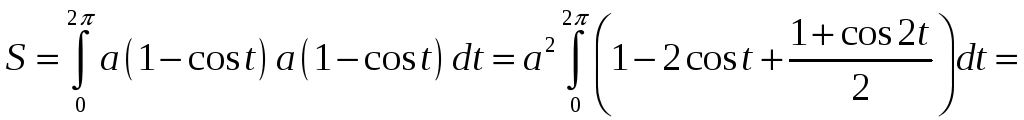
Площадь фигуры в полярной системе координат

Пусть в полярной системе координат задана функция , где – полярный радиус, – полярный угол. Пусть, далее, функция непрерывна при изменении угла в пределах ( и – в радианах). Фигура, ограниченная линией , с которой любой луч, исходящий из полюса , пересекается не более чем в одной точке, и двумя лучами и , называется криволинейным сектором.