Введение

Периодическими процессами называются процессы, при которых какая-либо физическая величина принимает многократно, через равные (или почти равные) последовательные промежутки времени, одни и те же (или приблизительно одни и те же) значения. Природа этой физической величины может быть самой различной. Например, это может быть отклонение шарика, подвешенного на нити, от положения равновесия, или угол, который составляет эта нить с вертикалью, или сила тока в электрическом контуре, или температура воздуха, повышающаяся в середине дня и понижающаяся ночью, или давление крови в сосудах при сокращениях сердца и т.д.

Рис. 1

Процесс, в течении которого некоторая физическая величина периодически отклоняется от некоторого значения в ту или иную сторону, называется колебанием.

Несмотря на различную природу, колебания самых

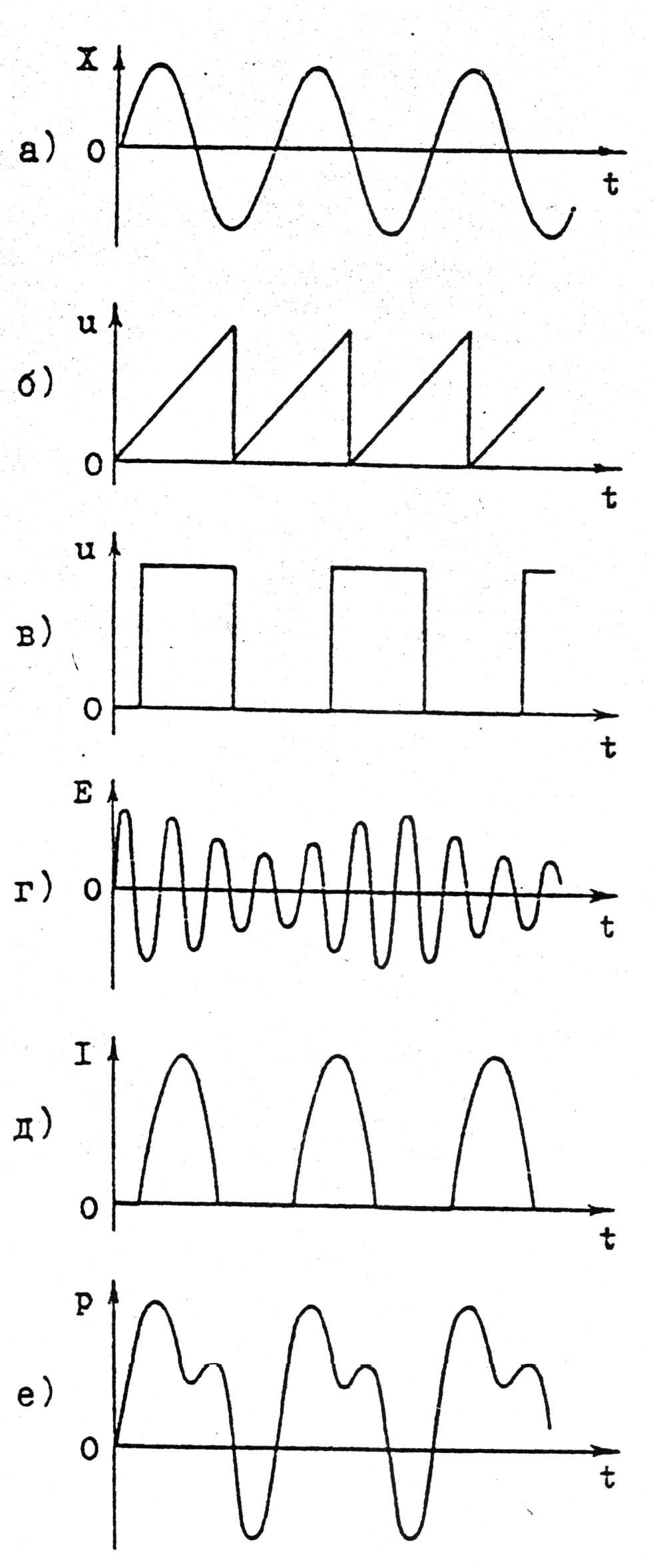
разнообразных величин имеют много общего. Все они характеризуются периодом - промежутком времени, через который значения колеблющейся величины начинают повторяться, амплитудой - наибольшим отклонением от нулевого значения. Часто при колебаниях изменение с течением времени различных по природе физических величин носит одинаковый характер, т.е. эти величины изменяются по одному и тому же закону с течением времени .В этом случае колебания описываются одинаковыми математическими формулами.

На рис. 1 показаны графики зависимости от времени некоторых из бесчисленно возможных периодических процессов для разных физических величин: а) отклонения x от положения равновесия груза, подвешенного на пружине, б) напряжения U, создаваемого генератором развертки электронного осциллографа, в) напряжения U , создаваемого генератором тактовой частоты компьютера, г) напряженности Е электрического поля, модулированного звуковой частотой, в радиоволне, д) силы I выпрямленного переменного тока, е) звукового давления p при произнесении звука « ууу...».

Общие для всех колебаний закономерности можно изучать на примере какой-либо одной физической величины. Далее в лабораторных работах 4, 5 и 5а мы будем рассматривать механические колебания. Механическими колебаниями называются такие колебания, для которых изменяющейся физической величиной является отклонение материальной точки (или системы материальных точек) от некоторого среднего положения ( для свободных колебаний - положения равновесия).

Работа 4 изучение свободных колебаний пружинного маятника

Цель работы. Определение коэффициента жесткости пружины по удлинению пружины и методом колебаний пружинного маятника.

Введение

Рассмотрим простейшую колебательную систему: груз массой m, подвешенный на пружине. Упругая сила растяжения пружины в положении равновесия равна силе тяжести груза и, будучи направлена вверх, уравновешивает ее. При выведении груза из положения равновесия пружина действует на него с дополнительной силой F, пропорциональной смещению x (при малых смещениях) и направленной в сторону, противоположную смещению:

,

где k —коэффициент жесткости пружины; он определяется численным значением силы, которую нужно приложить к пружине, чтобы растянуть (или сжать) ее на единицу длины. Единица измерения коэффициента жесткости

Груз, выведенный из положения равновесия, начнет совершать относительно него гармонические колебания :

, (1)

где A — амплитуда колебания; — фаза колебания;

— круговая частота; — начальная фаза колебания.

Энергия, сообщенная системе пружина—груз при начальном толчке, будет периодически преобразовываться: потенциальная энергия упруго деформированной пружины будет переходить в кинетическую энергию движущегося грузаобратно.

Согласно закону сохранения энергии для консервативной системы полная энергия

(2)

В момент прохождения грузом положения равновесия (x=0) из формулы (2) следует, что полная энергия системы

.

Согласно уравнению (1), скорость гармонически колеблющегося груза

,

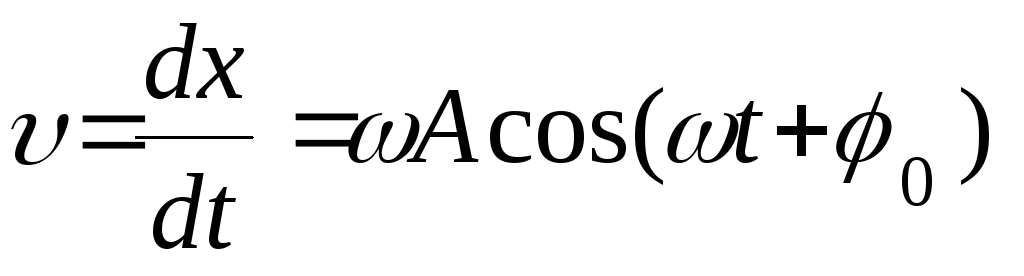а максимальная скорость

(3)

В крайних положениях груза (, x=±A) энергия системы переходит полностью в потенциальную :

.

По закону сохранения энергии

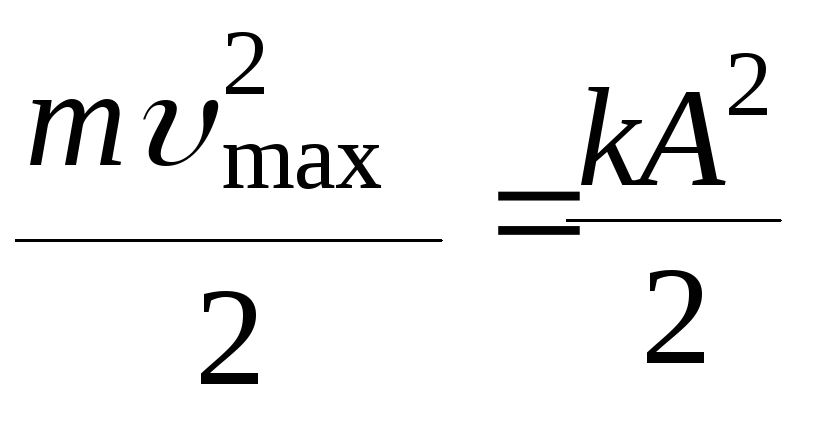. (4)

Подставляя выражение (3) в соотношение (4), получим

, .

Учитывая, что, получим выражение для периода колебаний T:

. (5)

Таким образом, при малых смещениях период не зависит от амплитуды колебаний и определяется только величинами m и k. Амплитуда и начальная фаза колебаний определяются начальными условиями, при которых возникло движение.

Приборы и принадлежности. Штатив с пружиной и зеркальной шкалой, держатель для грузов, набор грузов, секундомер.