Московский государственный университет

ПУТЕЙ СООБЩЕНИЯ (МИИТ)

Кафедра «Физика-2»

ОПТИКА

Работы 32, 33, 33а, 41, 42

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ЛАБОРАТОРНЫМ РАБОТАМ

по дисциплине

«Физика»

МОСКВА  2005

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПУТЕЙ СООБЩЕНИЯ (МИИТ)

Кафедра «Физика-2»

Утверждено

Редакционно-издательским

советом университета

ОПТИКА

Работы 32, 33, 33а, 41, 42

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ЛАБОРАТОРНЫМ РАБОТАМ

по дисциплине «Физика»

для студентов специальностей

УВМ, УПМ, УПО, УАИ, УИС, АТС, АТЭ, АЭЛ, ЭЭС, ЭЭТ, УПП, ТБЖ, ТРК, ВПО, ВОПУ, ВАТС, ВАУТ, ВЭС, ВЭЛТ, ВЭТ, ВУИ, ВУИТС

Под редакцией

доц. В. А. СЕЛЕЗНЕВА и доц. С. Г. СТОЮХИНА

МОСКВА 2005

УДК 539.2:621.382

М 54

Оптика. Работы № 32, 33, 33а, 41, 42: Методические указания к лабораторным работам по дисциплине “Физика”. / Под ред. доц. В.А.Селезнёва, доц. С.Г. Стоюхина. – М.: МИИТ, 2005. – 65 с.

Методические указания соответствуют программе и учебным планам по курсу общей физики, в них представлены: краткая теория, задания к пяти лабораторным работам по физике и методика их выполнения.

Авторы и составители: С.Г. Стоюхин (работа № 32),

Н.А. Гринчар, Т.В. Захарова (работы № 33 и 33а),

В.Г. Хавруняк, С.В. Мухин (работа № 41),

А.В. Пауткина (работа № 42).

 Московский государственный университет

путей сообщения (МИИТ), 2005

Работа 32

Определение длины световой волны при помощи бипризмы френеля

Цель работы. Изучение явления интерференции волн и определение длины волны света.

Приборы и принадлежности: Оптическая скамья с рейтерами, источник света со щелевой диафрагмой и светофильтрами, бипризма Френеля, окулярный микрометр, собирающая линза.

Введение

Современная теория о свойствах света утверждает, что свет имеет двойственную природу: свет рассматривается как электромагнитная волна и как поток корпускул.

Одно из важнейших явлений, иллюстрирующих волновые свойства света, - интерференция, заключается в том, что при наложении двух или нескольких волн интенсивность света в области суперпозиции световых пучков будет изменяться от точки к точке, достигая максимума, превышающего сумму интенсивностей пучков, и минимума, который может оказаться равным нулю. Для наблюдения устойчивой во времени интерференционной картины необходимо, чтобы источники света были когерентны.

Когерентностью называется согласованное протекание во времени и в пространстве нескольких колебательных или волновых процессов, проявляющееся при их сложении. В частном случае сложения волн одинаковой частоты, идущих от двух точечных источников, волны будут когерентными, если разность фаз в каждой точке пространства, где они встречаются, постоянна во времени. Источники, излучающие когерентные волны, также называются когерентными.

Два независимых источника света не могут быть когерентными, так как в данном случае излучения атомов не согласованы между собой по фазе, а кроме того, могут отличаться по частоте, так как процесс излучения в каждом из таких атомов длится очень короткое время, не превышающее стомиллионной доли секунды, а затем атом вновь начинает излучать световые волны, но уже с новой начальной фазой. Поэтому разность начальных фаз излучений двух независимых атомов будет изменяться при начале каждого нового акта испускания. В результате мы ни глазом, ни обычным физическим детектором не можем наблюдать мгновенные интерференционные картины, даваемые этими источниками, и видим лишь равномерную освещенность.

Существует два общих метода получения интерферирующих пучков из одного светового пучка. При одном из них пучок делится, проходя сквозь близко расположенные отверстия (метод деления волнового фронта), при другом методе пучок делится на одной или нескольких частично отражающих, частично пропускающих поверхностях (метод деления амплитуды).

Когерентные световые пучки монохроматического излучения, обладающие большой интенсивностью и направленностью распространения, можно получить и с помощью систем с вынужденным излучением. Соответствующие приборы, работающие в ультрафиолетовой, видимой и инфракрасной области спектра, называются “лазеры”.

В 1818 г. французский физик Френель осуществил опыт по интерференции двух световых пучков, идущих от одного источника. Опыт заключается в следующем: свет от источника S расходящимся пучком падает на призму, составленную как бы из двух призм I и II (рис. 1) с малыми преломляющими углами порядка 30’, которые сложены основаниями (бипризма).

Пучок света 1, 2 падает на первую половину бипризмы, а пучок 2, 3 - на вторую половину. При выходе из бипризмы пучок 1, 2 ограничивается лучами 1, 2, а пучок 2, 3 - лучами 2’, 3. В области OMN эти два пучка накладываются друг на друга и дают интерференционную картину на экране между точками M и N (см. рис. 1). Оба пучка, создающие интерференцию, как бы выходят из мнимых источников S₁ и S₂.

Характер интерференционной картины в какой-либо произвольной точке P (см. рис. 2) определяется соотношением между расстояниями от мнимых источников S₁ и S₂ до точки наблюдения P. (Предположим, что разность начальных фаз колебаний, излучаемых источником, равна нулю.) Тогда разность фаз лучей обусловливается расстояниями S₂P и S₁P и показателями преломления n сред, в которых распространяются лучи, то есть разностью оптических длин путей  _И  (SPn- SPn=-=). Если в разности оптических длин путей, которую называют разности хода , укладывается нечетное число полуволн, то для случая распространения лучей в воздухе (n= n= 1)

=S₂P–S₁P=(2m+1), (1)

где m = 0, 1, 2, 3, … - любое целое число,  - длина волны света в вакууме, то к точке P волны придут в противоположных фазах, и в этой точке будет наблюдаться минимум освещенности.

Во всех точках пространства, для которых разность хода равна четному числу полуволн, т.е.

=S₂P–S₁P=2m=m, (2)

наблюдается максимум освещенности.

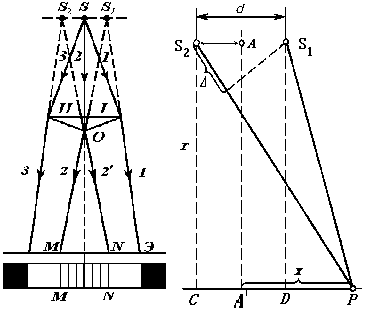
Рис.1 Рис.2

Если на пути монохроматических световых волн поставить экран Э, то он будет покрыт чередующимися светлыми и темными полосами. Переход от яркой к темной полосам будет происходить постепенно, так как постепенно, от точки к точке меняется разность хода лучей, дающих интерференцию в данной точке.

Расстояния между максимумами (или минимумами) освещенности (ширина полос) зависят от длины световой волны, дающей интерференционную картину.

Для определения соотношения между длиной волны и шириной полос рассмотрим в общем виде случай интерференции в воздухе (вакууме) волн, исходящих из двух когерентных источников S₁ и S₂, находящихся на расстоянии d друг от друга (см. рис. 2). Экран Э расположен на расстоянии r параллельно плоскости, в которой лежат мнимые источники S₁ и S₂ , при этом, точка A делит отрезок S₁S₂ пополам, а точка P, произвольно выбранная на экране Э, находится на расстоянии x от проекции точки А на плоскость экрана, то есть точки A’. Из геометрических соотношений не трудно определить разность хода волн, идущих из S₁ и S₂ и встречающихся в точке P, т.е. величину S₂P--S₁P.

Из S₁DP имеем:

(S₁P)²=r²+(DP)²=r²+(x–d/2)². (3)

Из S₂CP аналогично имеем:

(S₂P)²=r²+(CP)²=r²+(x+d/2)². (4)

Вычитая первое равенство из второго, получим

(S₂P)²–(S₁P)²=2xd. (5)

Представляя разность квадратов двух величин в виде произведения их суммы и разности, имеем:

S₂P–S₁P=.(6)

Вследствие малости расстояния x можно считать, что расстояние S₁P примерно равно расстоянию S₂P и, в свою очередь, равно r , т.е. с достаточной степенью точности можно положить, что

S₂P +S₁P2r; (7)

Тогда

S₂P – S₁P =xd/r.(8)

Для центров световых полос в интерференционной картине, получаемой на экране, согласно условию (2) имеем xd / r =m, т.е. световые полосы располагаются на расстояниях

x_m = mr/d (9)

от середины экрана. Расстояние между полосами m и (m+1)-го порядков равно

x = x_m+1 – x_m = - =. (10)

Полученное соотношение (10) дает возможность определить длину волны света  при известных расстояниях r, d и x:

 = x.(11)

Как видно из формулы (9), максимумы для лучей с наиболее короткой  (фиолетовых лучей) будут расположены ближе к центру, чем максимумы тех же порядков для лучей с наиболее длинной  (красных лучей). В середине экрана остается белая полоса (нулевой максимум; m=0). При освещении белым светом будет наблюдаться чередование цветных полос (спектр), так как положение максимумов и минимумов зависит от длины волны падающего света, и максимумы освещенности одного цвета (одной длины волны) могут совпадать с минимумами освещенности другого цвета.

В настоящей работе необходимо получить интерференционную картину при помощи бипризмы Френеля, произвести измерение расстояний r, d и x, вычислить длину волны света, дающего интерференционную картину.