Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный университет путей сообщения

Предмет:

Физика

Файл:

МАТЕР. по лекц. НИКИТЕНКО- физика. Ч.2 2013 / Лекции (Физика, часть II, л.1-4) 2013-II испр

..pdf

Скачиваний:

191

Добавлен:

09.06.2015

Размер:

1.17 Mб

Скачать

☆

1 / 41 2 3 4 > Следующая >>>

ФГБ ОУ ВПО «МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПУТЕЙ СООБЩЕНИЯ»

Кафедра «Физика»

С.М. Кокин, В.А. Никитенко

ФИЗИКА

Часть II

Рекомендовано редакционно-издательским советом университета в качестве учебного пособия

для студентов специальностей и направлений ИУИТ, ИТТСУ, ИПСС, ИЭФ, вечернего факультета

Москва – 2013

УДК 530.1 (076) К-55

Кокин С.М., Никитенко В.А. Физика. Часть II. Конспект лекций. – М.: МИИТ, 2013. – 178 с.

Учебное пособие представляет собой конспект лекций по общей физике, включающий разделы: «Колебания», «Волны», «Волновая и квантовая оптика», «Строение атома», «Молекулярная физика и термодинамика». В основу конспекта положен материал лекций, которые авторы читают в МИИТе для студентов ИУИТ и ИТТСУ.

Учебное пособие предназначено для студентов специальностей и направлений ИУИТ, ИТТСУ, ИПСС, ИЭФ, вечернего факультета.

Рецензенты:

–зав. кафедрой физики

–зав. кафедрой

Предисловие

Настоящее пособие является второй частью конспекта лекций по курсу общей физики, разрабатываемого проф. Кокиным С.М. и проф. Никитенко В.А. для информационных и связанных с электричеством специальностей и направлений университета. Часть III (Никитенко В.А., Кокин С.М. «Физика. Конспект лекций», разделы «Квантовая механика», «Элементы статистической физики», «Физические основы твердотельной микроэлектроники», «Ядерная физика. Элементарные частицы») вышла в 2007 г., часть I (Кокин С.М. «Физика. Конспект лекций», разделы «Механика», «Электростатика», «Постоянный электрический ток», «Магнетизм») появилась в 2010 г. и, наконец, часть II (2013 г.) замыкает логическую цепочку курса, представляя такие разделы, как «Колебания», «Волны», «Волновая и квантовая оптика», «Строение атома», «Молекулярная физика и термодинамика».

За время создания конспекта на смену рабочим программам 2-го поколения по физике пришли программы 3-го поколения ФГОС с сокращѐнными объѐмом часов и содержанием курса, появился бакалавриат. Всѐ это привело к существенному пересмотру содержания лекций, сделав их более ѐмкими, освободив от излишних деталей и выводов. Главным критерием стали простота и наглядность, чѐткая логика курса, умение рассказать простым языком о сложном.

Конспект не является самодостаточным изданием, он не заменит «живого» общения с лектором и восприятия лекций на слух, но поможет сэкономить время на лекциях при записи основных идей курса, при создании графиков, рисунков и т. д. Для освоения курса, конечно, необходимо посещать сами лекции с их многочисленными лекционными демонстрациями и мультимедийными приложениями, прорабатывать рекомендованную учебную литературу, а также контрольные задания и вопросы (изложенные в конце каждой лекции). Если говорить шире – полезно знакомиться с достижениями современной науки по научно-популярной литературе, журналам, интернет – публикациям, по библиотеке и фильмотеке Дома физики МИИТ.

Отдавая себе отчѐт в том, что первое издание конспекта не лишено недостатков, авторы с благодарностью примут все замечания. Просим направлять их по адресу: 127994, г. Москва, ул. Образцова, д. 9, стр. 9, МИИТ, кафедра «Физика» или fizikamiit@mail.ru.

Авторы

Лекция № 1 КОЛЕБАНИЯ. ЧАСТЬ I

1.1 Определения

Колебания – движения или процессы, повторяющиеся во времени.

Если одно и то же состояние системы повторяется через равные промежутки времени, то такие колебания называются пе-

риодическими.

Свободные (или собственные) – это гармонические периоди-

ческие колебания, совершающиеся за счѐт первоначально сообщѐнной энергии при отсутствии внешних воздействий. В реальных условиях свободные колебания всегда затухающие.

Гармоническими называются колебания, при которых физическая (или любая другая) величина x меняется со временем t по за-

кону косинуса (или синуса):
x Acos( 0t	0),	(1.1)

где A – амплитуда колебаний – модуль максимального значения x, 0 – круговая (циклическая) частота колебаний, ( 0t 0) – фаза колебаний, 0 – начальная фаза колебаний (фаза в момент време-

ни t 0).

Период колебаний – время T0,			за которое совершается одно
колебание; тогда 0	2	/T0 и измеряется в рад/с.
Линейная частота	0	1/T0 0/2	, измеряется в герцах: 1 Гц 1 с 1.

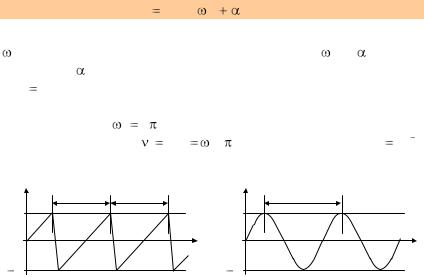
Примеры графиков негармонических периодических (а) и гар-

x	T0	T0		x	T0
A				A
0			t	0	t
A		а)		A	б)
		а)			б)

Рис. 1.1

монических (б) колебаний приведены на рис. 1.1.

Рис. 1.2

		Примечание 1
Гармонические колебания,			например, вида S		Acos( 0t		)
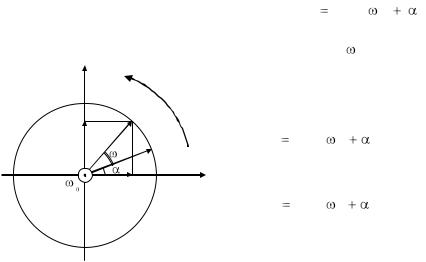
можно отображать с помощью проекций вектора					A ,	вращающе-
гося на плоскости с постоянной угловой скоростью						0 (см. рис.
			1.2). В процессе вращения про-
Y			екция этого вектора на ось OX
			совершает гармонические коле-
		A	бания:
AY			AX	Acos(	0t	);
	0t		AX	Acos(	0t	);
	0t		аналогичным образом меняется
			аналогичным образом меняется

		X	проекция вектора A и на ось OY:
	AX	X	проекция вектора A и на ось OY:
	AX
			AY	Asin(	0t	).

Описание гармонического колебания в виде проекций вращающегося вектора широко используется на практике для анализа результатов сложения нескольких

колебаний и носит название метода векторных диаграмм.

Примечание 2

При исследовании поведения реальных технических систем применяется метод, предложенный Фурье, следуя которому периодический процесс любой сложности представляется в виде совокупности гармонических колебаний, каждое из которых можно рассматривать независимо от других и описывать приведѐнными выше формулами. Такие колебания называются модами.

1.2 Примеры гармонических колебаний

Далее мы рассмотрим несколько систем, в которых наблюдаются гармонические колебания и убедимся в том, что, несмотря на их различия, процессы, происходящие в них, описываются оди-

наковыми математическими зависимостями.

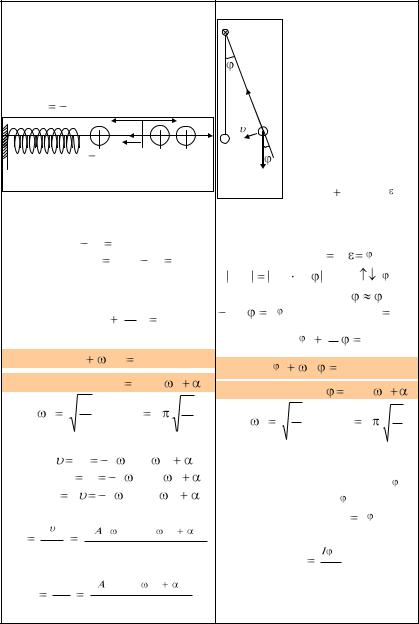
Пружинный маятник – груз мас- Математический

маятник

–

сой m, закреплѐнный на невесомой,

M mg

точечный

груз,

под-

абсолютно

упругой

пружине

вешенный на невесо-

жѐсткостью

совершающий

мой

нерастяжимой

колебания около

положения рав-

нити

совершающий

колебания

под

дейст-

новесия

под

действием

упругой

вием

силы

тяжести:

силы F

kx: рис. 1.3а.

рис. 1.3б.

Исходное уравнение –

основной

закон

ди-

m g

намики

вращатель-

Рис. 1.3а

ного движения:

Рис. 1.3б

= I

M mg

M T

Исходное уравнение – второй за-

( M

– момент силы тяжести m g ,

кон Ньютона, согласно которому:

ma,

M T

–момент силы

Так как

или (так как a

M T

x ),

m x .

Приведѐм полученное дифферен-

Mmg

mgl sin

, M mg

, и

циальное уравнение к канониче-

для малых углов sin

, то

0, или

mgl

I . А поскольку I

ml2,

скому виду: x

получаем:

0, или

(1.2)

Решение уравнения: x

Acos(

0), Решениеуравнения:

Acos(

0),

где

, или Т0

m .

где

, или Т0

Для шарика можно найти:

(формула Гюйгенса).

скорость

0sin(

0);

Пользуясь определениями, мож-

ускорение a

A 0

cos(

0);

но найти угловую скорость

импульс p

0msin(

0);

угловое ускорение

, момент

кинетическую энергию:

импульса маятника L

и его

2 sin 2 ( 0 t

0 )

кинетическую энергию

WК

потенциальную энергию:

kx 2

2 cos 2 (

WП

)

Заметим: период колебаний

математического маятника не

зависит от его массы!

Физический

маятник

Идеализированный

колебатель-

– твѐрдое

тело, совер-

ный контур – состоит из конден-

шающее колебания под

сатора

электроѐмкостью С и

действием

силы

тяже-

катушки

индук-

сти относительно

оси,

тивностью

(соп-

не

проходящей

через

ротивление цепи R

его центр тяжести: (Ц

0), рис. 1.3г.

на рис. 1.3в).

Исходное уравнение

m g

Исходное

уравнение –

EСИ

– закон Ома:

Рис. 1.3в

основной

закон дина-

Рис. 1.3г

EСИ,

мики

вращательного

движения:

= I .

где I – сила тока в

M mg

M N

цепи,

1 – разность потенциа-

( M mg – момент силы m g

M N

–

мо-

лов, EСИ – э.д.с. самоиндукции).

Так как EСИ

L I , I

q ,

мент силы реакции опоры

N ).

Так как

M N

q/(

2), и в контуре R

Mmg

mgd sin , причѐм M mg

получаем: 0

L q .

, и для малых углов sin

, то:

mgd

I .

Приведѐм уравнение к канони-

Приведѐм уравнение к канониче-

ческому виду: q

0, или

скому виду:

0, или

(1.2)

mgd

Решение уравнения:q

Acos(

0),

(1.2)

где

, или Т0

Решение уравнения:

Acos( 0t

0),

mgd

где

, или Т0

(формула Томсона); A

qмакс

mgd

Сила тока I

0sin(

0);

Здесь d – расстояние от центра

напряжение на конденсаторе

тяжести маятника до точки подвеса.

(

cos(

0),

Замечание 1: Так как момент инер-

ции I m, то период колебаний T

cos

(

0 t

0 )

от массы маятника не зависит.

его энергия WЭ

Замечание 2: Для вычисления I

энергия магнитного поля катушки

относительно

оси,

проходящей

LI 2

2 sin 2 (

через

точку

подвеса,

можно

ис-

WМ

)

пользовать теорему Штейнера.

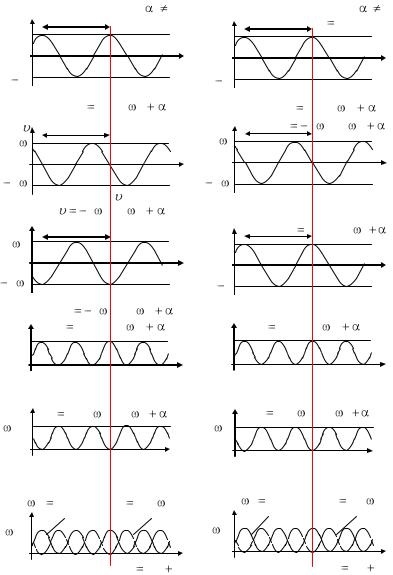
1.3 Графическое отображение получаемых результатов

Пружинный маятник (при 0

Колебательный контур (при

0 0)

qМАКС

Зависимость координаты x шарика

Зависимость заряда q конденсатора

от времени t:

Acos(

от времени t:

Acos(

0sin( 0t

A 0

Зависимость скорости шарика от

Зависимость силы тока I в катушке

времени t:

0sin(

индуктивности от времени t

(A/C)cos( 0t

Зависимость ускорения a шарика от

Зависимость напряжения U

времени t:

A 02cos( 0t

на конденсаторе от времени t

WП

[kA2cos2(

0)]/2

WЭ

[A2cos2(

0)]/2С

kA2/2

A2/2С

Зависимость потенциальной

Зависимость энергии WЭ

энергии WП пружины от времени t

конденсатора от времени t

WК

[mA2

02sin2(

0)]/2

WМ

[LA2

02sin2(

)]/2

mA2 02/2

LA2 02/2

Зависимость кинетической

Зависимость энергии WМ катушки

энергии WК шарика от времени t

индуктивности от времени t

Так как

k/m, то kA /2

0 /2

1/LC, то A /2C

0 /2

W, E

WП

WК

W, E

WЭ

WМ

mA2 02/2

LA2 02/2

Полная энергия маятника E

WП

WК

Полная энергия контура E

WЭ

WМ

со временем не меняется

Контрольные задания и вопросы

1.Дайте определение колебаний. Какие колебания называются периодическими, гармоническими, собственными?

2.Запишите уравнение гармонических колебаний. Сформулируйте определение амплитуды и фазы колебаний.

3.Выведите дифференциальное уравнение для свободных колебаний.

4.В чѐм заключается смысл метода векторных диаграмм?

5.Что называется пружинным маятником? Выведите формулу для расчѐта периода его колебаний.

6.Что называется математическим маятником? Выведите формулу для расчѐта периода его колебаний.

7.Что называется физическим маятником? Выведите формулу для расчѐта периода его колебаний.

8.Какая электрическая цепь является идеализированным колебательным контуром? Выведите формулу для расчѐта периода колебаний в этом контуре.

9.На примере пружинного маятника (и колебательного контура) дайте графическое отображение зависимости координаты (заряда, напряжения на конденсаторе), скорости (силы тока), ускорения, кинетической энергии (энергии магнитного поля катушки индуктивности), потенциальной энергии (энергии заряженного конденсатора) и полной энергии системы от времени протекания колебательного процесса.

Лекция № 2

КОЛЕБАНИЯ. ЧАСТЬ II

2.1 Затухающие колебания

Учтѐм теперь то, что в реальной системе всегда имеют место силы трения, сопротивления. Наличие таких сил отражается введением добавочных слагаемых в исходные формулы, описывающей поведение системы со временем (то есть в уравнения второго закона Ньютона, основного закона динамики вращательного движения, закона Ома). При небольших скоростях величина сил трения, сопротивления пропорциональна скорости движения тела: |FТР| | |, или |FТР| | x |, поэтому, с учѐтом того, что векторы скорости и силы сопротивления направлены в противоположные стороны, можно записать: FТР r x , где r – коэффициент сопротивления.

Уравнение второго закона Ньютона для пружинного маятника:

kx r x	m x .	(2.1)

Приведѐм данное дифференциальное уравнение к канониче-

0, и, обозначив

скому виду: x

2 m

получим:

(2.2)

Множитель

называется коэффициентом затухания; [

] c 1.

Рассмотрим

теперь

электрический

колебательный

контур

(рис. 2.1). Запишем для него формулу закона Ома и учтѐм, что в реальности сопротивлением R его элементов пренебречь нельзя:

EСИ, но EСИ

L I , I

q , I

q , С q/( 1

2),

причѐм 1

2 U, следовательно,

q R

L q .

(2.3)

Приведѐм данное дифференциальное уравне-

ние к каноническому виду:

q 0

EСИ

Рис. 2.1

1 / 41 2 3 4 > Следующая >>>

Соседние файлы в папке МАТЕР. по лекц. НИКИТЕНКО- физика. Ч.2 2013

#
09.06.201594.25 Кб412с. 230100.62 ИВТ ВМКС и ИВТ ПО,090900 ИБ БКС Никитенко вопросы 2с..pdf
#
09.06.20151.17 Mб191Лекции (Физика, часть II, л.1-4) 2013-II испр..pdf
#
09.06.2015351.23 Кб38ЛИТЕРАТУРА К ЛЕКЦИЯМ.doc
#
09.06.20152.45 Mб408Физика, часть III. Конспект лекций.pdf