№1 Электрическая цепь и ее элементы.

    Электрическая цепь представляет собой совокупность устройств, предназначенных для производства, передачи и потребления электрической энергии. Пример простейшей электрической цепи показан на рис. 1.1. Кружок со стрелкой внутри и стоящей рядом буквой Е (рис. 1.1, а) обозначает так называемый источник ЭДС (его еще называют источником напряжения). Это идеализированный источник энергии, внутреннее сопротивление которого равно нулю, а напряжение постоянно по величине, равно ЭДС реального источника и не зависит от протекающего по нему тока. Стрелка показывает направление возрастания потенциала внутри источника. Плюс находится у острия, минус – у хвоста стрелки. Ток во внешней цепи протекает по направлению стрелки ЭДС – от плюса источника к минусу. Внутреннее сопротивление реального источника R0 соединяется последовательно с ЭДС Е, и в совокупности они образуют схему замещения реального источника (на рис. 1.1, а обведена пунктиром).

    Другое представление схемы генератора осуществляется в виде параллельного соединения источника тока и сопротивления R0 (рис. 1.1, б). Под источником тока понимают также идеализированный источник энергии, внутреннее сопротивление которого бесконечно велико, и который вырабатывает ток J, не зависящий от величины нагрузки R и равный частному от деления ЭДС реального источника на его внутреннее сопротивление J = E/R0. На схеме он изображается кружком с двойной стрелкой, рядом с которым ставится буква J (рис. 1.1, б).

    В схеме рис. 1.1, а ЭДС равна сумме напряжений на нагрузке и внутреннем сопротивлении источника:

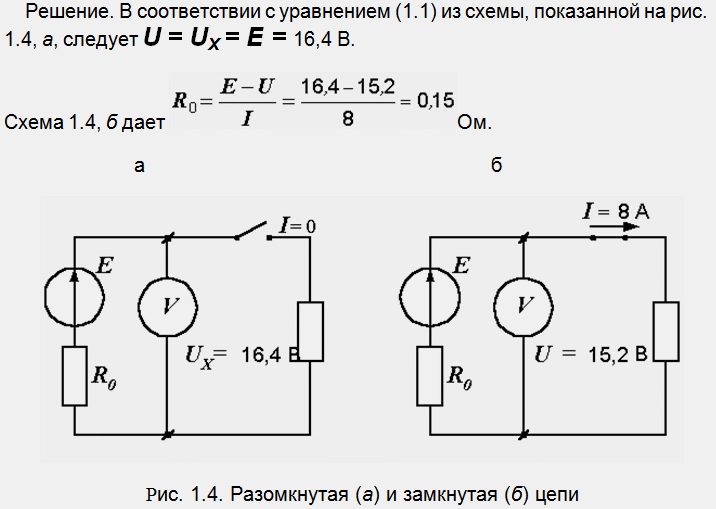
    Последнее выражение представляет так называемую внешнюю характеристику генератора. Оно говорит о том, что напряжение на его зажимах меньше ЭДС на величину падения напряжения на внутреннем сопротивлении (рис. 1.2). Чем больше ток и внутреннее сопротивление генератора, тем меньше выдаваемое им напряжение. При холостом ходе генератора (при I = 0) напряжение, измеренное на его разомкнутых зажимах равно ЭДС: U = E.

    На практике часто приходится сталкиваться с элементами схемы, показанными на рис. 1.3. Разница между ними заключается во взаимном направлении стрелок ЭДС и напряжения. В первом случае (рис. 1.3, а), когда эти стрелки направлены противоположно друг другу, напряжение определяется как разность потенциалов положительного и отрицательного зажимов источника и поэтому положительно. При одинаковых направлениях стрелок E и U (рис. 1.3, б) напряжение равно разности отрицательного и положительного потенциалов, а потому оно отрицательно: U = – E.

Пример 1.1. Напряжение холостого хода батареи равно 16,4 В. Чему равно ее внутреннее сопротивление, если при токе во внешней цепи, равном 8 А, напряжение на ее зажимах равно 15,2 В?

    При решении задачи мы полагали, что измерение проводилось идеальным вольтметром, имеющим бесконечно большое сопротивление. При конечной величине сопротивления вольтметра в измерение вносится погрешность.

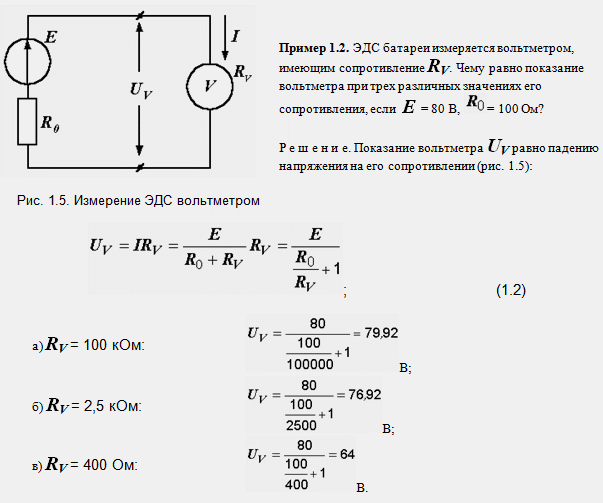
    Чем больше сопротивление вольтметра, тем меньше погрешность измерения. Как следует из формулы (1.2), только при RV →∞ показание вольтметра равно ЭДС: UV = E.

    Нагрузкой в схеме на рис. 1.1 служит сопротивление R. Напряжение на его зажимах связано с током законом Ома

    где G – проводимость, величина, обратная сопротивлению R; единица измерения – cименс (См).

    При G = const выражение (1.3) представляет собой уравнение прямой, проходящей через начало координат. Его график (рис. 1.6) называется вольтамперной характеристикой. Элементы электрической цепи, имеющие аналогичную (прямолинейную) вольтамперную характеристику, называются линейными. Электрическая цепь, состоящая только из линейных элементов, также называется линейной.

    Полагая в уравнении G=1/R (1.3), получим U = IR. Последнее выражение справедливо, когда стрелки напряжения и тока у резистора направлены в одну сторону (рис. 1.7, а). При изменении на схеме направления любой из стрелок в правой части закона Ома следует ставить минус (рис. 1.7, б). Здесь при определении напряжения на элементе мы "идем по стрелке" напряжения против стрелки тока.

    Рядом с буквой U можно ставить два индекса, обозначающие точки, между которыми определяется напряжение; например, Uab – напряжение между точками а и b. При этом направление стрелки напряжения на схеме определяется порядком следования индексов – от а к b (от первого индекса ко второму).

№2 Закон Ома для участка цепи с ЭДС.

    На практике часто встречается задача, когда требуется определить ток в некоторой ветви при известных ее параметрах и потенциалах ее зажимов.

    Между R и E отметим промежуточную точку с и выразим ее потенциал через потенциалы точек а и b.

    Так как в резисторе ток протекает слева направо, то потенциал точки а выше потенциала точки с на величину падения напряжения в активном сопротивлении:

    Точка b находится на положительном полюсе источника, а с – на отрицательном. Поэтому

    Беря разность левых и правых частей выражений (1.4) и (1.5), получим

    Для цепи на рис. 1.8, б после аналогичных рассуждений будем иметь

    В двух последних формулах ЭДС записывается с плюсом, если ее направление на схеме совпадает с направлением тока, и с минусом – в противоположном случае.

№3 Метод уравнений Кирхгофа.

    Этот метод сводится к решению системы уравнений, количество которых равно числу неизвестных токов (числу ветвей). Покажем его применение на примере схемы, изображенной на рис. 1.9.

    Первый закон Кирхгофа: в узле электрической цепи алгебраическая сумма токов равна нулю.

    Произвольно задавшись направлениями токов в ветвях и принимая токи, подтекающие к узлу, положительными, а оттекающие от узла – отрицательными, записываем:

    Число независимых уравнений в первом законе Кирхгофа – на единицу меньше числа узлов, поэтому для последнего узла d уравнение не пишем.

    В заданной схеме семь ветвей, семь неизвестных токов. Система (1.6) содержит только три уравнения. Недостающие четыре записываем по второму закону Кирхгофа.

    Второй закон Кирхгофа: в замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех сопротивлениях контура.

    Число уравнений, составляемых по этому закону, равно числу взаимно независимых контуров. При рассмотрении схемы каждый последующий контур является независимым относительно предыдущих, если он отличается от них хотя бы одной новой ветвью. В заданной схеме таких контуров четыре. Они отмечены пронумерованными дугообразными стрелками. Любой другой контур новых ветвей не содержит, поэтому не является независимым. Дугообразные стрелки показывают произвольно выбранные направления обхода контуров. Если направления ЭДС и токов совпадают с направлением обхода контура, то они записываются с плюсом, если не совпадают – то с минусом.

    Системы (1.6) и (1.7) дают достаточное количество уравнений для отыскания всех неизвестных токов.

№4 Метод узловых потенциалов.

    Уравнения, составляемые по этому методу, называются узловыми уравнениями. В качестве неизвестных они содержат потенциалы узлов, причем один из них задается заранее – обычно принимается равным нулю.

    Пусть таким узлом будет узел d: φ_d = 0. Равенство нулю какой-то точки схемы обычно показывается как ее заземление.

    Запишем для каждой ветви выражение закона Ома:

    Подставляя формулы (1.8) в систему (1.6) после несложных преобразований получаем следующие уравнения, количество которых на единицу меньше числа узлов:

    При решении практических задач указанный вывод не делают, а узловые уравнения записывают сразу, пользуясь следующим правилом.

    Потенциал узла, для которого составляется уравнение (например, в первом уравнении последней системы – это узел а), умножается на сумму проводимостей ветвей, присоединенных к этому узлу: φ_а*G1+G2+G3).Это произведение записывается в левой части уравнения со знаком плюс. Потенциал каждого соседнего узла (b и с) умножается на проводимости ветвей, лежащих между этим (соседним) узлом и узлом, для которого составляется уравнение.

    Эти произведения φ_b*(G1 + G2) и φ_с*G3 записываются со знаком минус. В правой части уравнения стоит алгебраическая сумма произведений ЭДС на проводимости тех ветвей, которые присоединены к рассматриваемому узлу: E1G1, E2G2 и E3G3. Эти произведения записываются с плюсом, если ЭДС направлены к узлу, и с минусом, если от узла.

    Найдя из (1.9) потенциалы узлов и подставляя их в (1.8), определяем токи ветвей.

№5 Метод контурных токов.

Для каждого из взаимно независимых контуров назначается так называемый контурный ток, замыкающийся по всем ветвям контура. Направления этих токов произвольны.     

На рис. 1.9 они обозначены дугообразными стрелками, рядом с которыми стоят буквы I_K1, I_K2, I_K3 и I_K4. Для выбранных контурных токов записываются уравнения по второму закону Кирхгофа. Контур при этом обходится по направлению контурного тока. Рассмотрим порядок составления уравнения на примере третьего контура. Контурный ток I_K3, протекая по сопротивлениям своего контура, создает на них падение напряжения    

    По сопротивлению R4, являющемуся элементом третьего контура, протекает контурный ток I_K2. Создаваемое им падение напряжения I_K2*R4 вычитается из предыдущего, так как направление тока I_K2 в сопротивлении R4 противоположно току I_K3. Сопротивление R6 также входит в третий контур. Падение напряжения на нем, создаваемое контурным током I_K4, складывается с суммой (1.10), так как направления I_K4 и I_K3 в R6 одинаковы. В правой части уравнения записывается алгебраическая сумма всех ЭДС контура, в данном случае – единственная ЭДС E4.

    Итак, для третьего контура имеем:

    Аналогично составляются и остальные контурные уравнения:

     После решения последней системы действительные токи ветвей определяются по найденным контурным:

    Контурные уравнения получаются подстановкой формул (1.11) в уравнения второго закона Кирхгофа (1.7).

№6 Метод наложения.

    В основе метода лежит принцип суперпозиции (наложения): ток в любой ветви сложной электрической цепи, содержащей несколько ЭДС, может быть найден как алгебраическая сумма токов в этой ветви от действия каждой ЭДС в отдельности.

    Это весьма важное положение, справедливое только для линейных цепей, вытекает из уравнений Кирхгофа и утверждает независимость действия источников энергии. Основанный на нем метод сводит расчет цепи, содержащей несколько ЭДС, к последовательному расчету схем, каждая из которых содержит только один источник.

    Например, токи в схеме на рис. 1.10, а находятся как алгебраические суммы частичных токов, определяемых из схем 1.10, б и в.

    При расчете подобных схем очень удобным оказывается следующий прием. Пусть требуется определить токи в параллельных ветвях при известном суммарном токе (рис. 1.11).

    Из полученной формулы вытекает правило: ток в одной из двух параллельных ветвей равен произведению общего тока на сопротивление соседней ветви, деленному на сумму сопротивлений параллельных ветвей.

    Применение этого правила избавляет от необходимости определять напряжения Uab` и Uab`` в схемах на рис. 1.10, б и 1.10, в. Так, после определения тока I1`, токи I2` и I3` можно найти по формулам:

№7 Эквивалентное преобразование треугольника и звезды сопротивлений.

    Пусть требуется рассчитать цепь, показанную на рис. 1.12, а.

    Расчет можно осуществить одним из описанных выше методов. Но так как в цепи имеется только один источник питания, наиболее простым было бы использование закона Ома. Однако попытка определения общего сопротивления цепи оказывается безрезультатной, так как здесь мы не находим ни последовательно, ни параллельно соединенных сопротивлений. Решить задачу помогает преобразование треугольника сопротивлений в эквивалентную звезду.

    Треугольник и звезда сопротивлений имеют вид, показанный на рис. 1.13.

    Если при замене одной из этих схем другой не изменяются потенциалы одноименных точек и подтекающие к ним токи, то во внешней цепи также не произойдет никаких изменений. В этом случае говорят, что схемы эквивалентны.

    Можно показать, что условием эквивалентности являются следующие уравнения:

    Например, сопротивление звезды R1, присоединенное к узлу 1, получается перемножением сопротивлений R12 и R31 треугольника, присоединенных к этому же узлу, и делением полученного произведения на сумму всех сопротивлений треугольника.

    При обратном преобразовании сопротивление треугольника R12, лежащее между узлами 1 и 2, равно сумме сопротивлений звезды R1 и R2, присоединенных к этим узлам, плюс их произведение, деленное на сопротивление третьего луча звезды R3.

    Пример 1.3. Рассчитать токи в цепи, изображенной на рис. 1.12, а, при следующих числовых значениях ее параметров: Е = 660 В, R1 = 20 Ом, R2 = 30 Ом, R3 = 5 Ом, R4 = 20 Ом, R5 = 50 Ом.

    а) Решение преобразованием треугольника в звезду.

    Теперь общее сопротивление цепи легко находится:

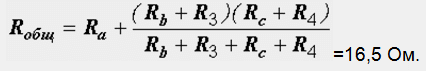
    Ток, протекающий по источнику (одинаковый в заданной и преобразованной схемах), равен:

    Ток в пятой ветви находим из первого закона Кирхгофа: I5 = I1–I3 = 26–28 = –2 A. Знак минус говорит о том, что действительное направление тока I5 противоположно указанному на схеме.

    б) Решение преобразованием звезды в треугольник.

    Преобразуем звезду, образуемую в схеме на рис. 1.12, а сопротивлениями R1, R5 и R3, в эквивалентный треугольник (рис. 1.12, в).

    Определяем сопротивления треугольника:

    Теперь рассчитываем преобразованную цепь. Сначала находим эквивалентные сопротивления участков ac и cd:

    Рекомендуем подставить в приведенные формулы числовые значения параметров цепи и сравнить результаты вычислений с полученными в примере 1.3а.

№8 Пассивный и активный двухполюсники. Теорема об активном двухполюснике.

     Двухполюсником называется часть электрической цепи любой сложности и произвольной конфигурации, выделенная относительно двух зажимов (двух полюсов).

     Двухполюсник, не содержащий источников энергии или содержащий скомпенсированные источники (суммарное действие которых равно нулю), называется пассивным. Если в схеме двухполюсника имеются нескомпенсированные источники, он называется активным. На схеме двухполюсник обозначают прямоугольником с двумя выводами (рис. 1.14). Это обозначение можно условно рассматривать как коробку, внутри которой находится электрическая цепь.

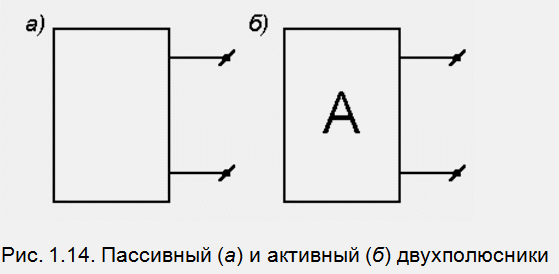
    Пассивный двухполюсник является потребителем энергии и может быть заменен эквивалентным сопротивлением, величина которого равна входному сопротивлению двухполюсника (см., например, рис. 1.15).

    Активный двухполюсник ведет себя как генератор. Находящиеся внутри него нескомпенсированные источники отдают энергию во внешнюю цепь (рис. 1.16, а). Можно попытаться подобрать источник энергии с ЭДС Е_Э и внутренним сопротивлением R_Э, который будет эквивалентен двухполюснику, то есть будет создавать во внешней цепи тот же самый ток (рис. 1.16, б).

    Полученный генератор должен быть эквивалентен двухполюснику в любом режиме, в том числе и в режимах холостого хода и короткого замыкания. Источники энергии, входящие в состав активного двухполюсника, в режиме холостого хода создают на его зажимах напряжение U_Х (рис. 1.17, а), а при коротком замыкании вызывают ток I_K (рис. 1.17, б).

    Из схем, приведенных на рис. 1.17, следует:

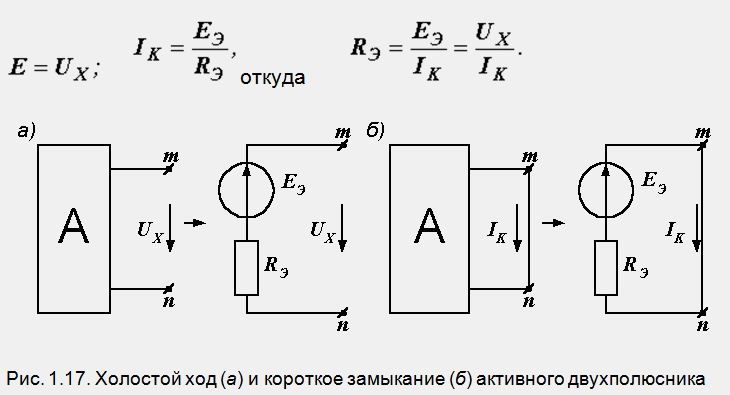
    Итак, любой активный двухполюсник может быть заменен эквивалентным генератором, ЭДС которого ЕЭ равна напряжению холостого хода двухполюсника, а внутреннее сопротивление RЭ напряжению холостого хода, деленному на ток короткого замыкания.

    Это утверждение и есть теорема об активном двухполюснике (эквивалентном генераторе).

     Пример 1.4. Заменить активный двухполюсник, выделенный пунктиром на рис. 1.18, а, эквивалентным генератором (рис. 1.18, б). Численные значения параметров цепи составляют: Е1 = 200 В, Е2 = 100 В, R1 = 50 Ом, R2 = 20 Ом, R3 = 20 Ом.

    Р е ш е н и е. Напряжение холостого хода, определяющее величину ЭДС эквивалентного генератора, можно найти по схеме на рис. 1.19, а любым известным способом.

    Воспользуемся, например, методом контурных токов. Принимая в качестве контурных токи I_1Х для левого контура и I_3Х для правого, записываем контурные уравнения, из которых определяем контурные токи:

    Напряжение холостого хода – это напряжение между точками m и n. Оно равно падению напряжения на сопротивлении R3:

    Ux=Umn=I_3X*R3=75 (B)

    Применим теперь метод узловых потенциалов.

    Принимая потенциал узла n равным нулю (φ_n = 0), для узла m запишем узловое уравнение:

    Получили тот же самый результат.

    Приступаем к расчету режима короткого замыкания. Ток IK в схеме на рис. 1.19, б найдем методом наложения. При действии только первой ЭДС ее ток проходит по первой ветви и, минуя вторую и третью ветви, замыкается по проводнику, закорачивающему зажимы двухполюсника:

    

№9 Метод эквивалентного генератора.

    Этот метод основан на сформулированной выше теореме (См. предыдущую лекцию) и применяется в тех случаях, когда требуется рассчитать ток в какой-либо одной ветви при нескольких значениях ее параметров (сопротивления и ЭДС) и неизменных параметрах всей остальной цепи.

    Сущность метода заключается в следующем. Вся цепь относительно зажимов интересующей нас ветви представляется как активный двухполюсник, который заменяется эквивалентным генератором, к зажимам которого подключается интересующая нас ветвь. В итоге получается простая неразветвленная цепь, ток в которой определяется по закону Ома.

    ЭДС Е_Э эквивалентного генератора и его внутреннее сопротивление R_Э находятся из режимов холостого хода и короткого замыкания двухполюсника.

    Порядок решения задачи этим методом рассмотрим на конкретном числовом примере.

    Пример 1.5. В цепи, показанной на рис. 1.20, а, требуется рассчитать ток I3 при шести различных значениях сопротивления R3 и по результатам расчета построить график зависимости I3(R3).

    Числовые значения параметров цепи: Е1 = 225 В; Е3 = 30 В; R1 = 3 Ом; R2 = 6 Ом.

    Р е ш е н и е.

    а) Расчет режима холостого хода.

    Убираем третью ветвь, оставляя зажимы m и n разомкнутыми (рис. 1.21, а). Напряжение между ними, равное U_X, находится как падение напряжения на сопротивлении R2:

    б) Расчет режима короткого замыкания. Замыкаем накоротко зажимы m и n (рис. 1.21, б). Ток короткого замыкания: Ik=E1/R1=75 (A)

    Внутреннее сопротивление эквивалентного генератора: Rэ=Ux/Ik=2 (Oм).

    Величину Rэ можно найти и другим способом. Оно равно входному сопротивлению двухполюсника при равенстве нулю всех его ЭДС. Если на рис. 1.21, а мысленно закоротить зажимы ЭДС Е1, то сопротивления R1 и R2 окажутся соединенными параллельно, и входное сопротивление цепи относительно зажимов m и n будет равно:

    Ток в полученной неразветвленной цепи №11 Закон электромагнитной индукции.

    Пусть имеется катушка, содержащая w витков (рис. 2.1) и помещенная в переменное магнитное поле.

    В каждом витке такой катушки индуцируется ЭДС электромагнитной индукции. Если магнитный поток, пронизывающий k-тый виток, обозначить Ф_k, то ЭДС этого витка будет равна:

    Так как все витки катушки соединены последовательно, то их суммарная ЭДС равна:

    Единица измерения потокосцепления такая же, как и у магнитного потока – вольт-секунда (Вс); Ее название – вебер (сокращенно Вб).

    Если все витки катушки, пронизываются одним и тем же магнитным потоком, т.е. если Ф₁ = Ф₂ = ... = Ф_k = Ф_w = Ф, то:

(рис. 1.20, б) определяется по закону Ома:

    Подставляя в последнюю формулу требуемые значения сопротивления R3, вычисляем ток и строим график (рис. 1.22).

    Данную задачу целесообразно решать именно методом эквивалентного генератора. Применение другого метода, например метода контурных токов, потребует решать систему уравнений столько раз, сколько значений тока необходимо найти. Здесь же всю цепь мы рассчитываем только два раза, определяя Еэ и Rэ, а многократно используем лишь одну простую формулу (1.13).

№10 Линия электропередачи постоянного тока.

     Если линия электропередачи имеет небольшую длину, при которой можно пренебречь утечкой тока через изоляцию, то ее электрическую схему можно представить в виде последовательного соединения сопротивления линии R_Л, равного суммарному сопротивлению прямого и обратного проводов, и сопротивления нагрузки R_Н (рис. 1.23).

     При анализе работы линии нас интересуют, главным образом, три вопроса: напряжение на нагрузке, величина передаваемой мощности и коэффициент полезного действия передачи. Режимы работы линии удобно рассматривать в виде зависимостей различных величин от тока в линии, равного :

     I=U1/(R0+R_H)

     Падение напряжения в линии ΔU и напряжение на нагрузке U2 определяются следующими выражениями:

     Если U1 и R_Л постоянны, то оба выражения представляют собой линейные функции тока (рис. 1.24). В режиме холостого хода (при I = 0) ΔU = 0, а U2 = U1. С ростом тока падение напряжения в линии возрастает, а напряжение на нагрузке уменьшается, и в режиме короткого замыкания (при R_Н= 0)

    Мощность на входе линии линейно зависит от тока: P1 = U1*I. При холостом ходе она равна нулю, а при коротком замыкании вычисляется по формуле

     Потери мощности в линии ΔP=I²Rл представляют собой квадратичную функцию тока. Ее график – парабола, проходящая через начало координат.

     Мощность, поступающая в нагрузку, равна разности мощности в начале линии и мощности, теряемой в проводах:

    Последнее выражение представляет собой уравнение параболы со смещенной вершиной и с обращенными вниз ветвями, проходящими через точки I = 0 и I = I_K.

    Мощность нагрузки представляет собой довольно сложную зависимость от сопротивления R_Н:

    При R_Н =0: Р2 = 0; при возрастании R_Н мощность Р2 сначала возрастает, достигает максимального значения и начинает убывать, стремясь к нулю при R_Н→∞ (рис. 1.25).

    Выясним, при каком сопротивлении нагрузки передаваемая ей мощность максимальна. Для этого продифференцируем функцию (1.15) по RН и приравняем ее к нулю:

     То есть мощность, получаемая нагрузкой, максимальна, когда сопротивление нагрузки равно сопротивлению линии.

    Ток, протекающий при этом по линии составляет половину тока короткого замыкания, а мощность в конце линии равна:

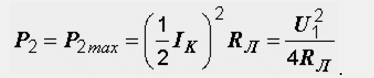
    Коэффициент полезного действия равен отношению мощностей в начале и конце линии:

    Из данной формулы следует, что коэффициент полезного действия передачи определяется отношением сопротивлений линии и нагрузки.

    При их равенстве, когда нагрузке передается максимальная мощность, η = 0,5 = 50 %. Этот режим, при котором теряется половина передаваемой энергии, на практике, естественно, не пригоден. В реальных линиях при передаче больших мощностей КПД составляет примерно 0,94–0,97. При этом сопротивление нагрузки значительно больше сопротивления линии.

    Для анализа режимов электропередачи полезной оказывается еще одна формула. Так как

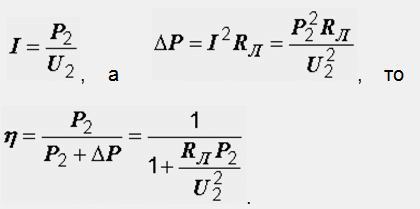
     То есть при одной и той же мощности нагрузки Р2, потери ΔР пропорциональны сопротивлению линии и обратно пропорциональны квадрату напряжения. Для увеличения коэффициента полезного действия передачи необходимо повышение напряжения и снижение электрического сопротивления проводов линии путем увеличения их сечения и применения материалов с меньшим удельным сопротивлением.

    Пример 1.6. Линия электропередачи с проводами марки А-120 длиной l = 1000 км питает нагрузку мощностью Р2 = 50 МВт. Каким должно быть напряжение в начале линии, чтобы КПД передачи был не ниже 90 %?

     Р е ш е н и е. Сопротивление одного километра провода марки А-120 R0 = 0,27 Ом/км. Суммарное сопротивление прямого и обратного проводов линии составляет RЛ = 2lR0 = 540 Ом.

    Принимая η = 0,9, из формулы (1.17) получаем:

    Для выполнения условий задачи напряжение в начале линии должно быть не ниже 548 кВ.

№11 Закон электромагнитной индукции.

    Пусть имеется катушка, содержащая w витков (рис. 2.1) и помещенная в переменное магнитное поле.

    В каждом витке такой катушки индуцируется ЭДС электромагнитной индукции. Если магнитный поток, пронизывающий k-тый виток, обозначить Ф_k, то ЭДС этого витка будет равна:

    Так как все витки катушки соединены последовательно, то их суммарная ЭДС равна:

    Единица измерения потокосцепления такая же, как и у магнитного потока – вольт-секунда (Вс); Ее название – вебер (сокращенно Вб).

    Если все витки катушки, пронизываются одним и тем же магнитным потоком, т.е. если Ф₁ = Ф₂ = ... = Ф_k = Ф_w = Ф, то:

№12 Получение синусоидальной ЭДС. Характеристики синусоидальных величин. Обозначения в цепях переменного тока.

    Пусть в однородном магнитном поле, например, между полюсами плоского магнита, под углом ψ к горизонтальной плоскости расположена плоская катушка, выполненная в виде прямоугольной рамки, по периметру которой намотано w витков (рис. 2.2). Площадь сечения рамки – S, магнитная индукция – В.

     Заставим эту катушку вращаться против часовой стрелки с угловой скоростью w . Если обозначить время полного оборота катушки через Т, то ω=2π/T, (рад/с) За некоторый промежуток времени t рамка повернется на угол ωt. Площадь проекции рамки в этом положении S_n=S*cos(ωt+ψ). Рамка и ее проекция на горизонтальную плоскую поверхность пронизываются одним и тем же числом силовых линий магнитной индукции, поэтому обусловленный ими магнитный поток равен:

    При вращении катушки число силовых линий, охватываемых ее витками, все время меняется.

    Например, при горизонтальном положении рамки это число максимально, при вертикальном – равно нулю. Другими словами, меняется магнитный поток, пронизывающий катушку, в результате чего в ней в соответствии с уравнением (2.2) наводится ЭДС:

    Поясним величины, входящие в последнее выражение. Еm – максимальное значение или амплитуда ЭДС. Аргумент синусоидальной функции ω ωt+ψ называется фазой. Угол ψ, определяющий начальное положение рамки и равный фазе в начальный момент времени (при t = 0), – начальная фаза. Фаза с течением времени (при вращении катушки) постоянно меняется. Скорость изменения фазы ω называется угловой или циклической частотой. Время одного цикла изменения фазы (время одного оборота рамки) называется периодом и обозначается T. Количество полных изменений синусоидальной ЭДС в секунду определяет частоту f, измеряемую в герцах (Гц). Один герц соответствует одному полному колебанию в секунду. Связь между частотой и периодом выражается формулой f= 1/T . При частоте 50 Гц: ω=2π/T=2πf=314(c^-1)

    Графическое изображение синусоидальной функции времени в электротехнике называют волновой диаграммой. При ее построении на горизонтальной оси откладывается время t или пропорциональный ему угол ωt. При нулевой начальной фазе кривая выходит из начала координат и через каждые четверть периода принимает максимальные значения и переходит через ноль. График такой функции построен по уравнению е = Еm sinωt на рис. 2.3, а.

    При ненулевых начальных фазах диаграммы имеют несколько иной вид. Пусть напряжение и ток на некотором участке цепи определяются выражениями:

    Для определенности положим ψ_u>0, а ψ_i<0. Сначала построим волновую диаграмму напряжения. При t = 0 u = Umsinψ_u. При положительном ψ_u эта величина положительна, и синусоида отсекает на вертикальной оси отрезок выше начала координат (рис. 2.3, б). Начало синусоиды и все ее точки оказываются сдвинутыми влево на величину ψ_u. Кривая тока, имея отрицательную начальную фазу, смещается вправо. Если начальные фазы двух синусоидальных функций, изменяющихся с одинаковой частотой, различны, то говорят, что они не совпадают по фазе. Отрезок на горизонтальной оси, разделяющий начала синусоидальных кривых (угол φ на рис. 2.3, б), определяет угол сдвига фаз. Он равен разности их начальных фаз:

    В случае напряжения и тока вычисление производится именно в таком порядке: начальная фаза напряжения минус начальная фаза тока.

    Еслиψ_u>ψ_i и угол φ положителен, то говорят, что напряжение опережает по фазе ток, или ток отстает по фазе от напряжения. На волновой диаграмме в этом случае кривая напряжения проходит через ноль и максимальные значения раньше тока; изменения тока отстают от соответствующих изменений напряжения. Мера отставания – угол φ.

    Остановимся еще на двух моментах. В цепях синусоидального тока мы будем встречаться как с переменными, так и с постоянными величинами. Для тех и других применяются различные обозначения. Переменные величины – функции времени – будем обозначать маленькими (строчными) буквами u, i, e, а постоянные – большими (прописными) U, I, Е.

    Второй момент касается указания направления тока или напряжения. При постоянном токе его направление связано с движением положительно заряженных частиц. В случае переменного тока его стрелка на схеме показывает у с л о в н о в ы б р а н н о е положительное направление. Если в какой-то момент времени ток направлен по стрелке, он считается положительным, в противном случае он отрицателен.

№13 Действующее значение переменного тока.

    Понятие действующего значения тока вводится в связи с необходимостью производства измерений. Что измерять у переменного тока? Если бы мы имели дело только с синусоидами – кривыми одной формы, то можно было бы измерять амплитуды. Но на практике встречаются самые разные кривые, и может оказаться так, что два различных по форме тока имеют одинаковые амплитуды, хотя очевидно, что на электрическую цепь они будут оказывать разное воздействие.

    Поэтому наиболее целесообразно оценивать величину тока по той работе, которую он совершает. При такой оценке действие переменного тока сравнивается с аналогичным действием постоянного тока. Например, если некоторый переменный ток выделяет на участке цепи такое же количество тепла, что и постоянный ток силой 10 ампер, то говорят, что величина этого переменного тока составляет 10 ампер. Это значение тока и называют действующим.

    Итак, действующим значением переменного тока называется численное значение такого постоянного тока, который за время, равное одному периоду, выделяет в сопротивлении такое же количество тепла, что и ток переменный..

    Таким образом, для оценки величины переменного тока мы должны сделать следующее.

    1.Определить количество теплоты, выделяющейся в сопротивлении R за время Т при протекании переменного тока i. Это количество теплоты равно:

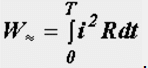
    2.Подобрать такой постоянный ток I, который за то же время Т в том же сопротивлении R выделяет такое же количество тепла. При постоянном токе оно равно: W=I²RT.

    3. Приравнять W=W:

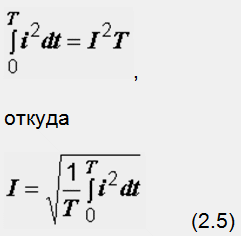
    Последняя формула и определяет действующее значение переменного тока.

    Пример 2.1. На вход некоторой цепи подается импульсное напряжение треугольной формы (рис. 2.4, а). Чему равно его действующее значение?

    Пример 2.2. На рис. 2.4, б показана кривая напряжения на выходе схемы однофазного однополупериодного выпрямления. Чему равно действующее значение напряжения, если его амплитудное значение Um составляет 311 В?

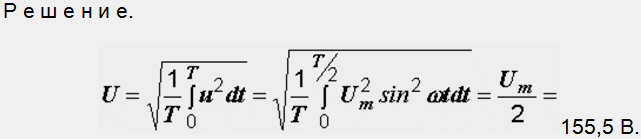
    Пример 2.3. Определить действующее значение синусоидального тока i=I_msin(ωt):

    Рассмотренные примеры показывают, что действующее значение переменного тока зависит от его формы.

Вращающимся вектором. Векторные диаграммы.

    Пусть в прямоугольной системе координат имеется вектор длиной I_m, расположенный под углом ψ к горизонтальной оси (рис. 2.5). Заставим этот вектор вращаться против часовой стрелки c угловой скоростью ω. Тогда за время t он повернется на угол ωt.

    Проекцию вектора на вертикальную ось обозначим i. Из треугольника oab она равна i=I_msin(ωt+ψ), т.е. представляет собой функцию, определяющую мгновенное значение тока. Таким образом, последняя может быть представлена как проекция на вертикальную ось вращающегося вектора. Изображение тока с помощью вектора называется его векторной диаграммой. Длина вектора может быть равна амплитудному I_m, либо действующему значению I.

    Обычно вектор при этом показывается не в произвольный момент времени t, а в начальный (t = 0), когда его угол наклона к горизонтальной оси равен начальной фазе.

    Теперь по уравнениям (2.3) построим векторную диаграмму двух векторов – тока и напряжения (рис. 2.6).

    Длины векторов равны действующим значениям, углы их наклона к горизонтальной оси – начальным фазам, а угол между векторами, равный разности начальных фаз ψ_u и ψ_i, в соответствии с уравнением (2.4) определяет сдвиг фаз напряжения и тока.

    Подчеркиваем, что на диаграмме стрелка, отмечающая угол φ, всегда направляется от вектора тока к вектору напряжения. Сейчас она направлена в положительном направлении – против часовой стрелки.

    Векторная диаграмма дает наглядное представление об отставании одних величин и опережении других. Если вращать картинку, показанную на рис. 2.6, против часовой стрелки, то вектор тока будет отставать от напряжения на угол φ. Так как при вращении длины векторов и угол между ними не меняются, то в том случае, когда начальные фазы напряжения и тока нас не интересуют, мы можем изображать диаграмму без осей и располагать ее так, как нам удобно (рис. 2.7).

№15 Основные сведения о комплексных числах.

    Комплексным числом называется выражение вида:

    где – c обозначение комплексного числа; a и b – соответственно действительная и мнимая части комплексного числа; j=√(-1) – мнимая единица.

    Величины a и b часто обозначают следующим образом: a = Re(c) , b = Im(c) . Символы Re и Im – есть начальные буквы английских слов Real – действительный и Imaginary – мнимый.

    Геометрически комплексное число изображается вектором на комплексной плоскости (рис. 2.8). Горизонтальная и вертикальная оси, отмеченные соответственно знаками +1 и +j, называются действительной (или вещественной) и мнимой. Действительная и мнимая составляющие комплексного числа представляют собой проекции вектора на эти оси.

    Два комплексных числа c и c` называются сопряженными, если они имеют одинаковые модули и равные по величине, но разные по знаку аргументы (рис. 2.10):

    Изображающие их векторы симметричны относительно вещественной оси.

    Действия над комплексными числами.

    Сложение и вычитание производится над числами, записанными в алгебраической форме:

    складываются по отдельности вещественные и мнимые части слагаемых:

    a=a₁+a₂; b=b₁+b₂

    Операции сложения комплексных чисел соответствует сложение изображающих их векторов.

    Сумма сопряженных комплексных чисел равна удвоенному значению вещественной части:

    Умножение и деление комплексных чисел удобнее всего производить в показательной форме. Модули при этом перемножаются или делятся, а аргументы складываются или вычитаются:

    Что происходит с векторами при перемножении комплексных чисел?

    На рис. 2.11 мы видим, что при умножении длина вектора возросла в с₂ раз, а аргумент увеличился на α₂.Рассматривая комплексное число как вектор, мы приходим к следующему выводу.

    При умножении вектора на комплексное число ае^jα , вектор растягивается в а раз и поворачивается на угол α .

    Произведение сопряженных комплексных чисел равно квадрату модуля комплексного числа:

    Иногда приходится производить умножение и деление комплексных чисел в алгебраической форме. Перемножение выполняется по правилам умножения многочленов с учетом того, что j² = -1

    При делении, чтобы получить результат, необходимо избавиться от мнимой единицы в знаменателе. Этого можно достичь умножением числителя и знаменателя на сопряженный знаменатель:

№16 Представление синусоидальных функций времени комплексными числами.

    Пусть задано выражение синусоидального тока i=I^msin(ωt+ψ). Как мы видели раньше, этому выражению соответствует вектор, длина которого равна I^m, а угол наклона к горизонтальной оси ψ. Если этот вектор изобразить в комплексной плоскости (рис. 2.13), то его можно обозначить комплексным числом Im=I^me^jψ, которое называется комплексной амплитудой тока.

    Комплексное действующее значение тока получается делением последнего выражения на √2 (корень из двух)

    

    Здесь и дальше буквами с точкой над ними (I, U, E) обозначаются комплексные числа, представляющие синусоидальные функции времени. Это ток, напряжение и ЭДС. Комплексные сопротивление и проводимость обозначаются прописными буквами Z и Y , а их модули строчными z и y. Комплексная мощность обозначается буквой S с волнистым значком ˜ (тильда) над ней.

№17 Способы задания синусоидального тока.

    Как следует из вышесказанного, синусоидальный ток можно задать четырьмя различными формами: уравнением i=I^msin(ωt+ψ) определяющим мгновенное значение тока (значение тока в любой момент времени), волновой диаграммой, вектором и комплексным числом. При этом мы легко можем перейти от одной формы задания к другой.

    В качестве начальной фазы мы берем не 120°, которые указаны на волновой диаграмме, а тот угол, на который сдвинуто начало синусоиды. Начальная фаза на волновой диаграмме определяется ближайшей к началу координат точкой перехода синусоиды через ноль от минуса к плюсу – это 60° . Так как начало синусоиды смещено от точки 0 влево, то начальная фаза положительна.

№18 Законы Кирхгофа в цепях синусоидального тока. Методы расчета цепей синусоидального тока.

    Для мгновенных значений ЭДС, токов и напряжений остаются справедливыми сформулированные ранее законы Кирхгофа.

    Первый: в любой момент времени алгебраическая сумма токов в узле электрической цепи равна нулю:

    Второй: в любой момент времени в замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме напряжений на всех остальных элементах контура:

    Токи, напряжения и ЭДС, входящие в уравнения (2.8) и (2.9), есть синусоидальные функции времени, которые мы рассматриваем как проекции некоторых векторов на оси координат. Так как сложению проекций соответствует сложение векторов и соответствующих им комплексных чисел, то справедливыми будут следующие уравнения, которые можно записывать как для действующих, так и для амплитудных значений.

    Из сказанного вытекают три возможных подхода к расчету цепей синусоидального тока: выполнение операций непосредственно над синусоидальными функциями времени по уравнениям выше; применение метода векторных диаграмм, использование в расчетах комплексных чисел и уравнений, являющихся основой символического метода.

    Пример 2.4. В узле электрической цепи сходятся три ветви (рис. 2.14).

    Обращаем внимание на то, что I¹+I²≠I³. Это не ошибка. В цепях синусоидального тока для показаний приборов законы Кирхгофа не справедливы. Можно складывать мгновенные значения токов (синусоидальные функции времени), векторы и комплексные числа, но не численные значения токов и напряжений, не показания приборов.

    Следует заметить, что первый из рассмотренных в примере методов из-за громоздкости вычислительных операций с синусоидами практически не применяется.

    Метод векторных диаграмм удобен при решении относительно несложных задач.

    В символической форме, как будет показано ниже, можно рассчитать сколь угодно сложную линейную цепь.

№19 Понятие об активном сопротивлении. Синусоидальный ток в активном сопротивлении.

    При протекании электрического тока выделяется энергия в виде тепла или механической работы. Параметр электрической цепи, характеризующий этот процесс, называется активным сопротивлением. Количественно он определяется следующим образом. Пусть на некотором участке цепи за время Т, равное периоду переменного тока, действующее значение которого I, необратимо преобразуется в тепло или механическую работу электрическая энергия W^Т. Тогда активное сопротивление рассматриваемого участка цепи по определению равно:

    На схеме активное сопротивление обозначается точно так же, как и сопротивление постоянному току (рис. 2.16). Последнее, называемое еще омическим, определяется структурой кристаллической решетки проводника и состоянием свободных электронов. Наличие вблизи каких-либо проводящих тел и ферромагнитных сердечников на омическое сопротивление не влияет.

    Иначе обстоит дело при переменном токе.

    При невысоких частотах сопротивление проводника мало отличается от сопротивления постоянному току. Но с повышением частоты все сильнее и сильнее сказывается поверхностный эффект, заключающийся в вытеснении переменного тока из серединных областей проводника к его поверхности. Это приводит к уменьшению сечения, занимаемого током, к увеличению сопротивления и возрастанию тепловых потерь. К аналогичным последствиям приводит и эффект близости, выражающийся в возникновении неравномерности распределения электрического тока по сечению проводника из-за действия магнитного поля соседних проводов.

    Если вблизи катушки имеются ферромагнитные сердечники и какие-либо другие проводящие тела, то магнитное поле переменного тока индуцирует в них вихревые токи, что вызывает дополнительные потери энергии на нагрев. Кроме того, в переменном магнитном поле происходит непрерывное периодическое перемагничивание ферромагнитного сердечника, требующее энергетических затрат на изменение направления магнитных моментов доменов.

    Таким образом, понятие активного сопротивления является более широким, по сравнению с омическим. Числитель в формуле (2.12) при переменном токе всегда больше, чем при постоянном, так как он включает в себя все перечисленные потери электромагнитной энергии на тепло. Поэтому для одной и той же электрической установки активное сопротивление переменному току всегда оказывается больше чем сопротивление постоянному току.

    Мгновенные значения напряжения и тока в активном сопротивлении связаны законом Ома:

    При изменении тока по синусоидальному закону

    напряжение тоже синусоидально и имеет с током одинаковые начальные фазы:

    Четыре последних уравнения представляют собой различные формы записи закона Ома для активного сопротивления.

    По уравнениям можно записать комплексные амплитуды тока и напряжения:

    Получили те же самые выражения закона Ома, но в символической форме.

    На показаны волновая и векторная диаграммы, построенные по формулам.

    В активном сопротивлении напряжение и ток совпадают по фазе; их начальные фазы одинаковы, угол сдвига фаз равен нулю, векторы на векторной диаграмме направлены в одну сторону (параллельны).

№20 Самоиндукция. Индуктивность. Синусоидальный ток в индуктивности.

    Если в катушке, изображенной на рис. 2.1, магнитное поле создается собственным током i, то магнитный поток называется потоком самоиндукции и обозначается Ф^L, а индуцируемая в катушке ЭДС е^L – ЭДС самоиндукции. В соответствии с формулой (2.1) она равна:

    где ψ – потокосцепление самоиндукции, величина, пропорциональная протекающему по катушке току: ψ = Li.

    Коэффициент пропорциональности L между потокосцеплением и током называется собственной индуктивностью или просто индуктивностью катушки (контура). Она зависит от формы и размеров катушки, а также от магнитной проницаемости сердечника. Ее размерность В x с/А=Ом x с. Эта единица измерения называется генри (Гн).

    Подставляя последнее выражение в (2.15) и полагая L = const, получаем следующую формулу, определяющую ЭДС самоиндукции:

    На рис. 2.18 показано изображение индуктивности на электрической схеме; u^L – напряжение на зажимах катушки, обусловленное электродвижущей силой самоиндукции, или другими словами, напряжение, наведенное в катушке собственным переменным магнитным полем.

    Все три стрелки на схеме (i, e^L, u^L) принято направлять в одну сторону. Раньше мы видели, что при одинаковых направлениях стрелок напряжения и ЭДС они имеют разные знаки. Поэтому:

    Знак минус в правой части формулы (2.16) обусловлен принципом Ленца, определяющим направление индуцированной ЭДС. В рассматриваемом случае он может быть сформулирован следующим образом:

    ЭДС самоиндукции направлена так, что своим действием препятствует причине, вызвавшей ее появление.

    Причина появления ЭДС самоиндукции – изменение тока. Поэтому при возрастании тока она направлена ему навстречу, при уменьшении тока – в одну с ним сторону.

    Препятствуя изменению тока, ЭДС самоиндукции оказывает ему сопротивление, которое называется индуктивным и обозначается х^L. В соответствии с формулой (2.16) его величина определяется индуктивностью и скоростью изменения тока, т.е. частотой. Формула, определяющая индуктивное сопротивление, имеет вид:

    В цепях постоянного тока такого понятия мы не встречали, так как при постоянных магнитных полях ЭДС самоиндукции не возникает. Пусть ток, протекающий по индуктивности, определяется выражением (2.13). Тогда напряжение на ее зажимах, в соответствии с формулой (2.17), равно:

    Это – мгновенное значение напряжения. Его амплитуда равна:

    Аналогичное выражение получается (после деления на √2) и для действующих значений:

    Уравнения, связывающие напряжение и ток в индуктивности, как в вещественных, так и в комплексных числах, представляют собой закон Ома для индуктивности.

    Начальная фаза напряжения больше начальной фазы тока на 90° . В индуктивности ток отстает от напряжения на четверть периода. Выражение закона Ома, записанное в символическое форме, указывает на этот сдвиг фаз. Вспомним, что умножение вектора на j приводит к его повороту на угол 90° против часовой стрелки.

    Согласно уравнениям (2.18) U^L получается путем умножения произведения Ix^L на j, в результате чего вектор U^L оказывается повернутым относительно вектора I.

    Пример 2.5. Мгновенное значение напряжения на индуктивности определяется выражением u^L = 200 sin(ωt+60°)В. Записать выражение мгновенного значения тока, если L = 63,67 мГн, а частота питающего напряжения f = 50 Гц. Построить векторные диаграммы напряжения и тока.

    Решение. При частоте f = 50 Гц циклическая частота ω = 314 с_-1, и индуктивное сопротивление x^L = ωL = 20 Ом. Амплитуда тока равна:

    Так как в индуктивности ток отстает от напряжения на четверть периода, его начальная фаза меньше начальной фазы напряжения на 90° : ψⁱ = ψ^u – 90° = 60–90–30°.

    Итак, i = 10sin (ωt–30°). Векторная диаграмма показана на рис. 2.20.

№21 Синусоидальный ток в емкости.

    Система из двух проводящих тел, разделенных диэлектриком, образует конденсатор. Эти проводящие тела называются обкладками. Если к ним подключить источник энергии, то на них будет накапливаться заряд q, пропорциональный напряжению на конденсаторе u_c

    Коэффициент пропорциональности C между зарядом и напряжением называется емкостью конденсатора. Единица измерения емкости – фарада (Ф). Она имеет следующую размерность: Кл/В=А*с/В=с/Ом=Ом^-1*с. Емкость зависит от формы, размеров конденсатора и от диэлектрической проницаемости диэлектрика между обкладками. Пусть напряжение, подаваемое источником на конденсатор, изменяется по закону:

    u_c=U_cmaxsin(ωt+ψ)

    При его возрастании от нуля до максимального значения конденсатор заряжается, на его обкладки от источника поступает электрический заряд. При уменьшении напряжения от максимума до нуля, заряд стекает с конденсатора, он разряжается. Таким образом, в проводах, соединяющих конденсатор с остальной цепью, постоянно движется электрический заряд, т.е. протекает электрический ток. Вывод о наличии электрического тока мы делаем, совершенно не касаясь вопроса о том, какие процессы происходят между обкладками конденсатора. Величина тока определяется зарядом, прошедшим в единицу времени через поперечное сечение проводника:

    Она зависит от емкости и скорости изменения питающего напряжения, т.е. от частоты. От этих же факторов зависит и электрическая проводимость участка цепи с конденсатором. Ее называют емкостной проводимостью и определяют по формуле:

    B_c=ωC=2πfC

    Величина, обратная емкостной проводимости, называется емкостным сопротивлением:

    Подставляя в предыдущую формулу приложенное к конденсатору напряжение, получаем:

    Действующее значение тока:

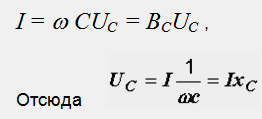
    Последние три уравнения представляют разные формы записи закона Ома для конденсатора. Запишем их в символической форме:

    Векторная диаграмма, построенная по приведенным выше уравнениям, показана на рисунке далее.

    наклона каждого вектора к положительному направлению вещественной оси определяется начальными фазами в выражениях выше. Так как при определении напряжения U_c мы умножаем Ix_cна -j, то вектор U_c оказывается повернутым относительно вектора тока на угол 90град. в отрицательном направлении, по часовой стрелке. Как отмечалось раньше, направление угла φ на диаграмме показывается от вектора тока к вектору напряжения.

    

    Пример 2.6. Напряжение на конденсаторе u_C = 100sin (1000t –30°). Написать выражение мгновенного значения тока через конденсатор. Каким станет ток, если частота питающего напряжения увеличится вдвое? Емкость конденсатора С = 50 мкФ.

    Решение. Определяем емкостное сопротивление:

№22 Последовательное соединение активного сопротивления, индуктивности и емкости.

    В схеме, состоящей из последовательно соединенных активного сопротивления, индуктивности и емкости (рис. 22.1), заданы приложенное напряжение U, частота f и числовые значения параметров R, L и С. Требуется найти ток и напряжения на элементах.

    При анализе электрических цепей синусоидального тока типична ситуация, когда метод решения незнакомой задачи неизвестен. Во многих случаях помогает следующий подход. По установленным ранее правилам строится векторная диаграмма, из анализа которой выводятся необходимые расчетные формулы. Так же поступим сейчас и мы.

    В последовательной цепи общим для всех элементов является протекающий по ним ток, поэтому именно с него начинаем построение векторной диаграммы. Проводим его изображение горизонтально (рис. 22.2).

    Вообще, направление первого вектора при построении диаграмм произвольно. Оно диктуется соображениями удобства. Дальше мы должны показать векторы напряжений на всех элементах и в соответствии со вторым законом Кирхгофа в векторной форме U=U_R+U_L+U_C получить вектор входного напряжения. Сложение векторов можно выполнять по правилу параллелограмма, однако удобнее применять правило многоугольника, когда каждый последующий вектор пристраивается к концу предыдущего.

    Нам известно, что напряжение на активном сопротивлении совпадает по фазе с током, поэтому вектор U_R мы направляем по вектору I. К его концу пристраиваем вектор U_L и направляем его вверх, так как напряжение на индуктивности опережает ток на 90°. Напряжение U_С находится в противофазе с U_L, т.е. отстает от тока на тот же угол 90°, поэтому вектор UС, пристроенный к концу вектора UL, направлен вниз. Векторная сумма U_R, U_L и U_С дает вектор приложеного напряжения U.

    Величины напряжений на отдельных элементах цепи нам известны:

    Из треугольника oab (рис. 22.2) по теореме Пифагора находим:

    Вынося из под знака радикала, записываем последнее выражение в виде: U=I*z; где,z - полное сопротивление.

    В последней формуле разность индуктивного и емкостного сопротивлений мы обозначили буквой х. Это общее реактивное сопротивление цепи: х = х_L – x_C. Сами индуктивность и емкость называются реактивными элементами, и их сопротивления х_L и x_C тоже носят названия реактивных.

    Выражение U=Iz называется законом Ома для всей цепи. Оно может быть записано и так: I=U/z=Uy.

    где, y– полная проводимость цепи, представляющая величину, обратную полному сопротивлению 1/z

    Если необходимо определить угол сдвига фаз между напряжением и током, то это можно сделать из треугольника напряжений oab (рис. 22.2):

    Векторная диаграмма на рис. 22.2 построена для случая, когда U_L>U_C, что имеет место при X_L>X_C, когда в цепи преобладает индуктивность, и цепь носит активно-индуктивный характер. Общий ток отстает по фазе от входного напряжения.

    Возможны также режимы, когда U_L<u_{C и UL=UC</u}

№23 Параллельное соединение активного сопротивления, индуктивности и емкости.

    Рассмотрим схему, состоящую из параллельно соединенных активного и реактивных элементов (рис. 23.1, а).

    Требуется по известным G, В_L, В_C, U рассчитать токи. Как и прежде, задачу будем решать двумя методами.