Методички / Эффект Холла (Кули-Заде) / Эффекта Холла модифицированная 21-04

ИЗУЧЕНИЕ ЭФФЕКТА ХОЛЛА

Цель работы: Измерение холловской разности потенциалов в полупроводниковой пластине и определение концентрации, подвижности и знака носителей заряда, участвующих в токе.

Введение

Эффект Холла-это возникновение поперечной разности потенциалов при пропускании тока через металлическую или полупроводниковую пластинку, помещенную в магнитное поле, таким образом, чтобы вектор индукции магнитного поля ( ) было направлено перпендикулярно вектору плотности тока ( ).

C помощью эффекта Холла (1879 г.) можно измерить зависимость плотности тока от концентрации свободных электронов.

Сущность эффекта Холла, на основе классической электронной теории, заключается в следующем. Если проводник, по которому течет ток, поместить в магнитное поле, то на заряды движущиеся в магнитном поле действует сила Лоренца, направленная перпендикулярно их движению. Если, например, электроны движутся в прямоугольном проводнике на рис. 1 влево, то направленное в плоскость чертежа магнитное поле будет действовать силой, направленной вверх. В результат электроны будут двигаться вверх, а положительные заряды к нижней поверхности проводника.

Вследствие этого между поверхностями проводника А и В возникает разность потенциалов. Она будет увеличиваться до тех пор, пока не наступит равновесное состояние, при котором сила холловского электрического поля станет раной магнитной силе Лоренца:

Рис.1

(1)

Или

Так как магнитное поле направлено перпендикулярно к линиям тока, то напряженность поперечного электрического поля равна по абсолютной величине

(2)

Тогда разность потенциалов поперечного электрического поля между поверхностями проводника

(3)

где d-расстояние между поверхностями А и В проводника.

Средняя скорость направленного движения носителей тока связана с плотностью тока j соотношением j=nqV_d , где n- концентрация носителей заряда(число носителей в единице объема, q-заряд носителя). Следовательно,

(4)

Выразив плотность тока через силу тока I:

(5)

(b-толщина пластины) и подставив выражения (5) и (4) в (3), получим

(6)

(7)

Коэффициент называют постоянной Холла.

Формула (7) получена без учёта закона распределения электронов по скоростям. Более точный расчет с учетом закона распределения носителей по скоростям в рамках классической статистики приводит к выражению для постоянной Холла

(8)

В полупроводниках с атомной решеткой, например для кремния,

поэтому

Для полупроводников с ионной связью, например для интерметаллического соединения арсенида галлия А=1. В этом случае применима формула (7).

Соотношение (6) позволяет определить постоянную Холла и концентрацию носителей заряда n, в образце из опытных данных

(9)

Если известно, то, измеряя и I, можно найти . Этот способ измерения используется в технике (датчики Холла).

Важной характеристикой полупроводника является подвижность в нем носителей заряда, под которой подразумевается средняя скорость, приобретаемая носителем в поле, напряженность которого равна единице. Если в поле напряженностью носители приобретают скорость , то подвижность их u, равна

(10)

Используя связь между плотностью тока, напряженностью электрического поля и проводимостью и учитывая (4) и(10), можно выразить подвижность через проводимость σ и концентрацию носителей заряда:

(11)

Из соотношений (7) и(11) следует

(12)

Таким образом, для определения подвижности носителей, необходимо измерить и σ.

Из (7) следует, что знак постоянной Холла совпадает со знаком носителей заряда. У полупроводников постоянная Холла может быть отрицательной и положительной, так как существует два типа проводимости. У полупроводников с электронной проводимостью( полупроводников n-типа) знак постоянной Холла отрицателен. Если электропроводимость полупроводников осуществляется положительными зарядами или так называемыми «дырками», то знак постоянной Холла положителен. Такие полупроводники называются дырочными (полупроводниками р-типа). Если в полупроводнике одновременно осуществляется оба типа проводимости, то по знаку постоянной Холла можно судить о том, какой из них является преобладающими.

Зависимость знака постоянной Холла от знака носителей заряда, создающих в данном веществе можно понять из рис.2, на котором демонстрируется эффект Холла для образцов с положительными и отрицательными носителями.

Рис.2

Направление силы Лоренца изменяется на противоположное как при изменении направления движения зарядов, так и при изменении знака.

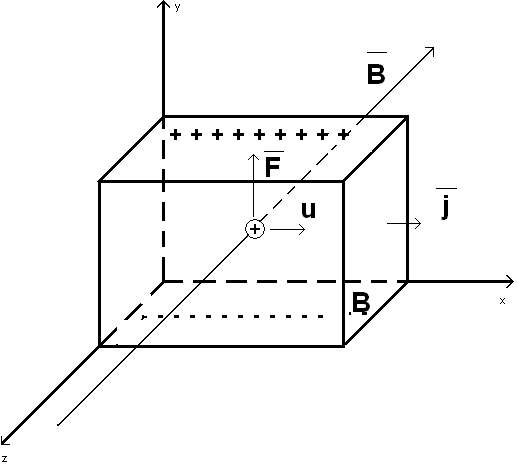
Следовательно, при одинаковом направлении тока и магнитной индукции ( ) сила Лоренца, действующая на положительные и отрицательные носители, имеет одинаковое направление.