95

Открытое акционерное общество «Российские железные дороги»

ПЕРВАЯ РЕДАКЦИЯ

УПРАВЛЕНИЕ РЕСУРСАМИ, РИСКАМИ НА ЭТАПАХ ЖИЗНЕННОГО ЦИКЛА И АНАЛИЗОМ НАДЁЖНОСТИ В ХОЗЯЙСТВЕ ЖЕЛЕЗНОДОРОЖНОЙ АВТОМАТИКИ И ТЕЛЕМЕХАНИКИ

Учебное пособие

Москва 2012

СОДЕРЖАНИЕ

ВВЕДЕНИЕ 5

1 ОСНОВНЫЕ ПОКАЗАТЕЛИ, МОДЕЛИ И МЕТОДЫ ОЦЕНКИ НАДЁЖНОСТИ, ИСПОЛЬЗУЕМЫЕ В МЕТОДОЛОГИИ УРРАН. 7

1.1. Показатели и количественные характеристики надежности 7

1.2. Типовые примеры и их решения 18

1.3. Расчет показателей надёжности невосстанавливаемых нерезервированных систем 20

1.3.1 Методы расчета 20

1.3.2. Типовые примеры и их решения 25

1.4 Методология УРРАН и особенности её применения в хозяйстве железнодорожной автоматики и телемеханики 28

2 ПРИМЕНЕНИЕ МЕТОДОЛОГИИ УРРАН НА ЭТАПЕ ПРОЕКТИРОВАНИЯ СИСТЕМ ЖЕЛЕЗНОДОРОЖНОЙ АВТОМАТИКИ И ТЕЛЕМЕХАНИКИ 33

2.1 Термины, допущения и задачи применения методологии УРРАН на этапе проектирования систем ЖАТ 33

2.2 Последовательность применения методологии УРРАН для систем ЖАТ на этапе проектирования 36

2.3 Структурные методы расчёта надёжности устройств и систем ЖАТ 38

2.4 Определение проектных показателей надёжности систем ЖАТ с учётом условий эксплуатации 40

2.4.1 Представление исходных данных 40

2.4.2 Определение проектной интенсивности отказов эталонного объекта в фактических условиях эксплуатации 44

2.4.3 Определение значений проектных показателей надёжности функционирования системы ЖАТ в фактических условиях эксплуатации 48

3 АНАЛИЗ ПОКАЗАТЕЛЕЙ НАДЁЖНОСТИ СИСТЕМ ЖЕЛЕЗНОДОРОЖНОЙ АВТОМАТИКИ, ТЕЛЕМЕХАНИКИ И СВЯЗИ НА ЭТАПЕ ЭКСПЛУАТАЦИИ НА ОСНОВЕ МЕТОДОЛОГИИ УРРАН 52

3.1 Постановка задачи 52

3.2 Оценка достигнутых показателей надёжности системы ЖАТ 53

3.2.1 Общие положения 53

3.2.2. Сбор и представление исходных данных 63

3.2.3. Получение статистических оценок интенсивности отказов систем ЖАТ и интенсивности их восстановлений 67

3.2.4 Проверка адекватности теоретического распределения 73

3.2.5. Интервальная оценка средней интенсивности отказов и средней интенсивности восстановлений 76

3.2.6. Оценка тенденции в изменении интенсивностей отказов и восстановлений системы железнодорожной автоматики и телемеханики 78

3.2.7. Оценка средней наработки на отказ и среднего времени до восстановления 79

3.3 Анализ достигнутых показателей надёжности систем ЖАТ на этапе эксплуатации 80

3.3.1 Постановка задачи 80

3.3.2 Сценарии управления надёжностью 81

4 РАСЧЁТ И АНАЛИЗ ПОКАЗАТЕЛЕЙ НАДЁЖНОСТИ УСТРОЙСТВ ЖАТ ДЛЯ ЗАДАННОГО ПОЛИГОНА НА ОСНОВЕ МЕТОДОЛОГИИ УРРАН 94

5 ПРИМЕНЕНИЕ МЕТОДОЛОГИИ УРРАН ПРИ ОЦЕНКЕ РИСКОВ ДЛЯ СИСТЕМ ЖЕЛЕЗНОДОРОЖНОЙ АВТОМАТИКИ И ТЕЛЕМЕХАНИКИ 106

ПРИЛОЖЕНИЕ 1 116

ПРИЛОЖЕНИЕ 2 125

ПРИЛОЖЕНИЕ 3 131

ПРИЛОЖЕНИЕ 4 134

ПРИЛОЖЕНИЕ 5 140

ПРИЛОЖЕНИЕ 6 143

ПРИЛОЖЕНИЕ 7 147

ПРИЛОЖЕНИЕ 8 149

ПРИЛОЖЕНИЕ 9 152

ПРИЛОЖЕНИЕ 10 154

Введение

В настоящее время ОАО «Российские железные дороги» заинтересовано в повышении конкурентоспособности на долгосрочный период. Наряду с иными мероприятиями, достижение указанной цели базируется на выявлении и использовании резервов в существующей инфраструктуре. В управлении своей эксплуатационной деятельностью компания ориентируется на методологию обеспечения безотказности, готовности, ремонтопригодности и безопасности (RAMS). Цель внедрения данной методологии заключается в сокращении стоимости жизненного цикла объектов инфраструктуры при условии обеспечения высокого уровня надёжности технических средств и требуемого уровня безопасности перевозочного процесса. При этом сами уровни надёжности и безопасности определяются исходя из допустимых величин издержек на реализацию перевозочного процесса, а также на ликвидацию возможных последствий.

С целью решения задачи рационального использования материальных ресурсов и обеспечения требуемых параметров перевозочного процесса в рамках концепции RAMS реализуется методология комплексного управления надёжностью, рисками, стоимостью жизненного цикла на железнодорожном транспорте (УРРАН), позволяющая проводить анализ работы систем железнодорожной автоматики и телемеханики (ЖАТ) и других объектов транспортной инфраструктуры при различных условиях эксплуатации.

Методология УРРАН позволяет анализировать эффективность функционирования систем и устройств ЖАТ с различным уровнем детализации такого анализа, в частности, выполнять оценку на этапе проектирования целесообразности применения той или иной системы ЖАТ на конкретном участке железной дороги, выносить оценку о качестве проведения технического обслуживания систем ЖАТ на различных уровнях (станция, перегон, цех, линейно-производственный участок, дистанция, дорога, сеть дорог в целом) хозяйства автоматики и телемеханики, планировать эксплуатационные затраты на содержание систем и устройств ЖАТ с целью минимизации стоимости жизненного цикла.

1 Основные показатели, модели и методы оценки надёжности, используемые в методологии урран.

1.1. Показатели и количественные характеристики надежности

Показатель надежности – характеристика одного или нескольких свойств, составляющих надежность объекта.

Основные термины и определения, используемые в теории надежности и концепции RAMS приведены в Приложении 10.

К числу наиболее широко применяемых показателей надежности относятся:

• вероятность безотказной работы в течение определенного времени ;

• средняя наработка до первого отказа ;

• наработка на отказ ;

• частота отказов ;

• интенсивность отказов ;

• параметр потока отказов ;

• коэффициент готовности .

Характеристикой надежности будем называть количественное значение показателя надежности конкретного изделия.

Выбор количественных характеристик надежности зависит от вида изделия.

Основные показатели надежности можно разбить на две группы:

• показатели, характеризующие надежность невосстанавливаемых изделий;

• показатели, характеризующие надежность восстанавливаемых изделий.

Невосстанавливаемыми называются такие изделия, для которых в рассматриваемой ситуации проведение восстановления работоспособного состояния не предусмотрено в нормативно-технической и (или) конструкторской документации. Если происходит отказ такого изделия, то выполняемая операция будет сорвана, и ее необходимо начинать вновь в том случае, если отказ можно устранить. К таким изделиям относятся изделия однократного действия, такие как ракеты, управляемые снаряды, искусственные спутники Земли, а также системы многократного действия, такие как системы управления воздушным и железнодорожным движением, системы управления химическими, металлургическими и другими ответственными производственными процессами.

Восстанавливаемыми называются такие изделия, для которых в рассматриваемой ситуации проведение восстановления работоспособного состояния предусмотрено в нормативно-технической и (или) конструкторской документации. Если произойдет отказ такого изделия, то он вызовет прекращение функционирования изделия только на период устранения отказа. К таким изделиям относятся: телевизор, агрегат питания, локомотив, автомобиль и т. п.

На рис. 1.1 показан временной график работы невосстанавливаемых и восстанавливаемых изделий.

Рисунок 1.1. Временной график работы невосстанавливаемых и восстанавливаемых изделий:

а) – изделия невосстанавливаемые (- время непрерывной работы, Н.О – начало операции, К.О – коней операции);

б) – изделия восстанавливаемые (- время исправной работы,- время вынужденного простоя).

Рассмотрим следующую модель испытаний. На испытании находится изделий, и испытания считаются законченными, если все они отказали. Причем отказавшие изделия отремонтированными или новыми не заменяются. Тогда показателями надежности данных изделий являются:

• вероятность безотказной работы ;

• частота отказов ;

• интенсивность отказов ;

• средняя наработка до первого отказа ;

Вероятность безотказной работы выражает вероятность того, что в пределах заданной наработки отказ изделия не возникнет.

Вероятность безотказной работы по статистическим данным об отказах оценивается согласно выражению

(1.1)

где – количество изделий, отказавших к моменту времениt, при их исходном количестве ;- статистическая оценка вероятности безотказной работы. При большом числе изделийстатистическая оценкапрактически совпадает с вероятностью безотказной работы . На практике иногда более удобной характеристикой является вероятность отказа.

Вероятность отказа - вероятность того, что при определенных условиях эксплуатации в заданном интервале времени произойдет хотя бы один отказ. Отказ и безотказная работа являются событиями несовместимыми и противоположными, поэтому

, . (1.2)

Частотой отказовназывается отношение числа отказавших изделий в единицу времени к первоначальному числу изделий при условии, что все вышедшие из строя изделия не восстанавливаются.

Частоту отказов по статистическим данным об отказах оценивается согласно выражению

(1.3)

где – число отказавших изделий в интервале времени отдо.

Частота отказов есть плотность вероятности (или закон распределения) времени работы изделия до первого отказа. Поэтому

,,. (1.4)

Интенсивностью отказов называется отношение числа отказавших изделий в единицу времени к среднему числу изделий, исправно работающих в данный отрезок времени.

Согласно определению интенсивность отказов по статистическим данным об отказах определяется

(1.5)

где - среднее число исправно работающих изделий в интервале;– число изделий, исправно работающих в начале интервала; – число изделий, исправно работающих в конце интервала .

Интенсивность отказов есть условная плотность вероятности возникновения отказа невосстанавливаемого изделия, определяемая для рассматриваемого момента времени при условии, что до этого момента отказ не возник.

Вероятностная оценка этой характеристики находится из выражения

(1.6)

Интенсивность отказов и вероятность безотказной работы связаны между собой зависимостью

(1.7)

Средней наработкой до отказа называется математическое ожидание наработки изделия до первого отказа.

Как математическое ожидание вычисляется через частоту отказов (плотность распределения времени безотказной работы):

. (1.8)

Так как t положительно и , а, то

. (1.9)

По статистическим данным об отказах средняя наработка до первого отказа вычисляется по формуле

(1.10)

где – время безотказной работыi- го изделия, - число испытуемых изделий.

Как видно из формулы (1.10), для определения средней наработки до первого отказа необходимо знать моменты выхода из строя всех испытуемых изделий. Поэтому для вычисления пользоваться указанной формулой неудобно. Имея данные о количестве вышедших из строя изделийв каждомi-ом интервале времени, среднюю наработку до первого отказа лучше определить из выражения

. (1.11)

В выражении (1.11) иm находятся по следующим формулам

, ,

где - время началаi-ого интервала; - время концаi-ого интервала; - время, в течение которого вышли из строя все изделия;- интервал времени.

При изучении надежности технических устройств часто применяются следующие законы распределения времени безотказной работы: экспоненциальный, нормальный, Релея, Гамма, Вейбулла.

В табл. 1.1 приведены выражения для оценки количественных характеристик надежности изделий при указанных законах распределения времени безотказной работы.

Таблица 1.1. Основные соотношения количественных характеристик надежности при различных законах распределения времени безотказной работы

Закон распределения	Частота отказов	Вероятность безотказной работы	Интенсивность отказа
Экспоненциальный
Релея
Вейбулла
Нормальный
Гамма

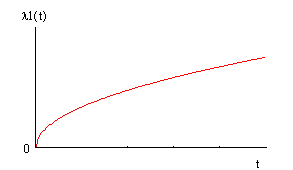
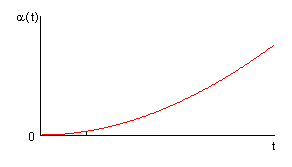
Из выражений для оценки количественных характеристик надежности видно, что все характеристики являются функциями времени. На рис. 1.2 приведены зависимости количественных характеристик надежности изделий от времени.

а
б
в
г
д

Рисунок 1.2. Зависимость количественных характеристик от времени

а) экспоненциальная модель; б) модель Релея; в) модель Вейбулла;

г) модель нормального распределения; д) модель гамма распределения

Рассмотренные показатели надежности позволяют достаточно полно оценить надежность невосстанавливаемых изделий. Они также позволяют оценить надежность восстанавливаемых изделий до первого отказа.

Наличие нескольких показателей вовсе не означает, что всегда нужно оценивать надежность изделия по всем показателям.

Наиболее полно надежность изделия характеризуется частотой отказов . Это объясняется тем, что частота отказов является плотностью распределения, а поэтому несет в себе всю информацию о случайной величине – времени безотказной работы.

Средняя наработка до первого отказа является достаточно наглядной характеристикой надежности. Однако применение этого показателя для оценки надежности сложной системы ограничено в тех случаях, когда:

• время работы системы гораздо меньше среднего времени безотказной работы;

• закон распределения времени безотказной работы не однопараметрический;

• система резервированная;

• интенсивность отказов непостоянная;

• время работы отдельных частей сложной системы разное.

Интенсивность отказов - наиболее удобная характеристика надежности простейших элементов, так как она позволяет более просто вычислить количественные характеристики сложной системы.

Наиболее целесообразным показателем надежности сложной системы является вероятность безотказной работы. Это объясняется следующими особенностями вероятности безотказной работы:

• она входит в качестве сомножителя в другие более общие характеристики системы, например в эффективность и стоимость;

• характеризует изменение надежности во времени;

• может быть получена сравнительно просто расчетным путем в процессе проектирования системы и оценена в процессе ее испытания.

В табл.1.2 показана взаимосвязь между показателями надежности.

Таблица 1.2 Взаимосвязь между показателями надежности

Известно	Требуется определить
	-
		-
			-
				-

Рассмотрим показатели надёжности восстанавливаемых систем.

Средняя наработка на отказ есть отношение наработки восстанавливаемого изделия к математическому ожиданию числа его отказов в течение этой наработки.

Эта характеристика определяется по статистическим данным об отказах по формуле

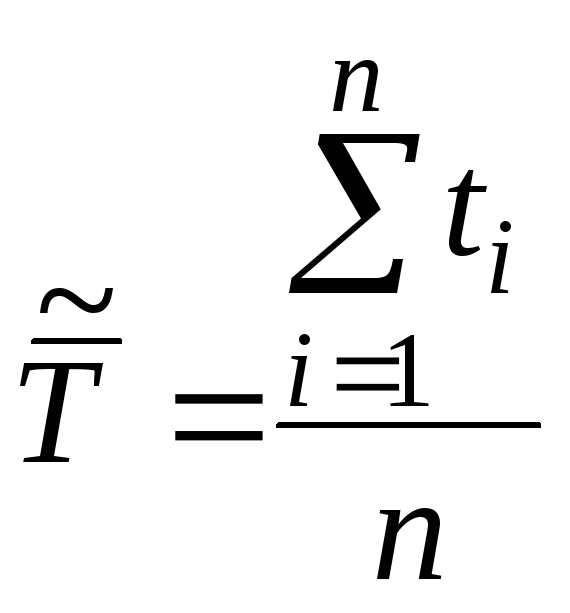, (1.13)

где - время исправной работы изделия между (i – 1)-м и i-м отказами; n – число отказов за некоторое время t.

Из формулы (1.13) видно, что в данном случае наработка на отказ определяется по данным испытания одного образца изделия. Если на испытании находится N образцов в течение времени t, то наработка на отказ вычисляется по формуле

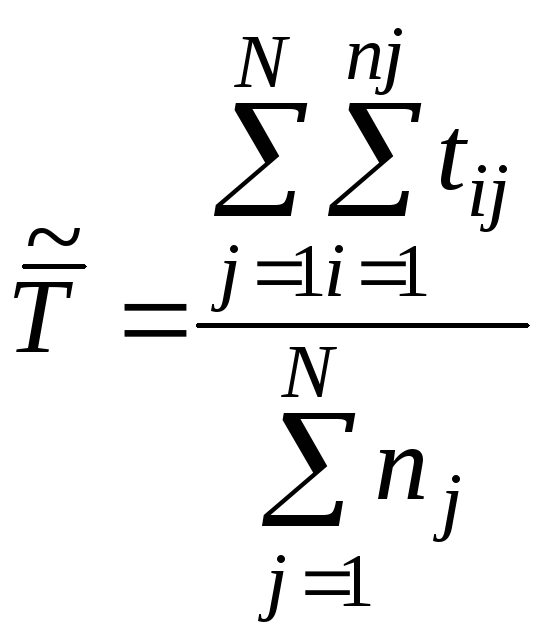, (1.14)

где - время исправной работыj-го образца изделия между (i – 1)-м и i-м отказом; - число отказов за времяt j-го образца.

Наработка на отказ является достаточно наглядной характеристикой надежности, поэтому она получила широкое распространение на практике.

Параметр потока отказов и наработка на отказ характеризуют надежность ремонтируемого изделия, но не учитывают времени, необходимого на его восстановление. Поэтому они не характеризуют готовности изделия к выполнению своих функций в нужное время. Для этих целей вводятся такие показатели, как коэффициент готовности и коэффициент вынужденного простоя.

Коэффициент готовности есть вероятность того, что изделие окажется в работоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается.

Эта характеристика определяется по статистическим данным как отношение времени исправной работы к сумме времен исправной работы и вынужденных простоев изделия, взятых за один и тот же календарный срок. Эта характеристика обозначается .

Согласно данному определению

(1.15)

где – суммарное время исправной работы объекта; – суммарное время вынужденного простоя.

Времена и вычисляются по формулам

, , (1.16)

где - время работы изделия между (i – 1)-м и i-м отказом; - время вынужденного простоя послеi-го отказа; n – число отказов (ремонтов) изделия.

Для перехода к вероятностному показателю величины изаменяются математическими ожиданиями времени между соседними отказами и времени восстановления соответственно.

Тогда

, (1.17)

где - среднее время наработки на отказ;- среднее время восстановления.

Среднее время восстановления есть математическое ожидание времени восстановления работоспособного состояния объекта.

Как математическое ожидание вычисляется через частоту восстановления (плотность распределения времени восстановления):

, (1.18)

где - частота восстановления, равная, (- вероятность восстановления).

По статистическим данным среднее время восстановления вычисляется по формуле:

(1.19)

Коэффициентом вынужденного простоя называется отношение времени вынужденного простоя к сумме времен исправной работы и вынужденных простоев изделия, взятых за один и тот же календарный срок.

Согласно определению

(1.20)

или переходя к средним величинам,

(1.21)

Коэффициент готовности и коэффициент вынужденного простоя связаны между собой зависимостью

. (1.22)

При анализе надежности восстанавливаемых систем обычно коэффициент готовности вычисляют по формуле

(1.23)

Формула (1.23) верна только в том случае, если поток отказов простейший, и тогда .

Часто коэффициент готовности, вычисленный по формуле (1.23) отождествляют с вероятностью того, что в любой момент времени восстанавливаемая система исправна. На самом деле указанные характеристики неравноценны и могут быть отождествлены при определенных условиях.

Поэтому вводится понятие функции готовности, которая определяется из выражения:

, (1.24)

где ;.

Кроме установившегося коэффициента готовности часто используется среднее значение этого коэффициента за интервал времени

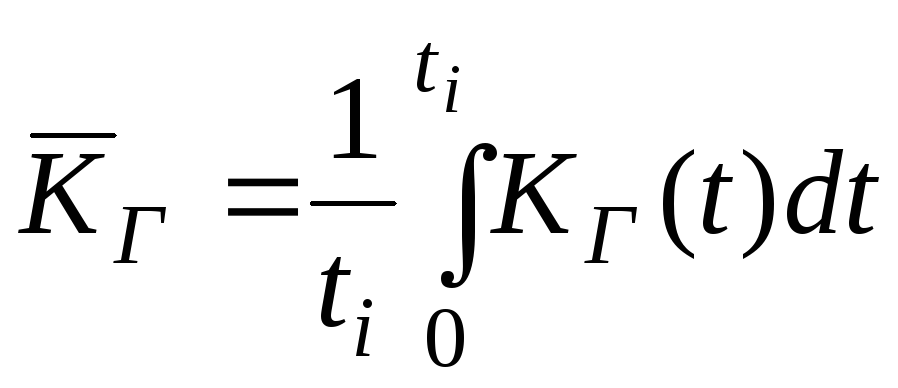(1.25)

Коэффициент оперативной готовности - вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается, и, начиная с этого момента, будет работать безотказно в течение заданного интервала времени

Согласно определению

(1.26)

Коэффициент оперативной готовности оценивает не только готовность системы к выполнению заданных функций, но и способность выполнять функции определенной временной протяженностью.