Надежность_1 / poz115

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный университет путей сообщения

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

λс = ∑n λi = 0,00007 + 0,00005

+ 0,00004 + 0,00006 + 0,00004 = 0,00026 час-1

= 3846 час

.pdf

Скачиваний:

132

Добавлен:

09.06.2015

Размер:

1.87 Mб

Скачать

☆

1 / 41 2 3 4 > Следующая >>>

Федеральное агентство по образованию

Государственноеобразовательноеучреждениевысшегопрофессиональногообразования

Ухтинский государственный технический университет

Кафедра промышленной безопасности и охраны окружающей среды

ОСНОВЫ РАСЧЁТА НАДЁЖНОСТИ

Методические указания для практических занятий для студентов специальности 280102 «Безопасность технологических

процессов и производств»

Ухта 2008

УДК 614:551.521 (076.5) Н 82

Нор, Е.В.

Основы расчёта надёжности [Текст]: метод. указания для практических занятий / Е.В. Нор, Е.С. Бердникова. – Ухта: УГТУ, 2008. – 37 с.

Методические указания предназначены для практических занятий по дисциплине «Надёжность технических систем и техногенный риск» для студентов специальности 280102.65 «Безопасность технологических процессов и производств».

Методические указания рассмотрены и одобрены кафедрой ПБ и ООС от 19.06.08 протоколом № 8.

Рецензент: Бердник А.Г., доцент кафедры ПБ и ООС, к.т.н. Редактор: Колесник О.А., ассистент кафедры ПБ и ООС.

В методических указаниях учтены предложения рецензента и редактора.

План 2008 г., позиция 115.

Подписано в печать 18.12.2008 г. Компьютерный набор. Объём 37 с. Тираж 50 экз. Заказ № 226.

©Ухтинский государственный технический университет, 2008 169300, Республика Коми, ул. Первомайская, д. 13.

Отдел оперативной полиграфии УГТУ.

169300, Республика Коми, г. Ухта, ул. Октябрьская, д. 13.

	СОДЕРЖАНИЕ
1 Расчёт показателей надёжности нерезервированных невосстанавливаемых
систем ...............................................................................................................................		4
1.1	Методы расчёта показателей надёжности .............................................................	4
1.2	Примеры решения задач ..........................................................................................	5
1.3	Задачи для самостоятельного решения ................................................................	16
2 Расчёт показателей надёжности резервированных невосстанавливаемых
систем ............................................................................................................................		19
2.1	Методы расчёта показателей надёжности ...........................................................	19
2.1.1 Общее резервирование с постоянно включенным резервом ..........................		19
2.1.2 Общее резервирование замещением .................................................................		21
2.1.3 Раздельное резервирование ................................................................................		22
2.1.4 Резервирование с дробной кратностью .............................................................		23
2.1.5 Скользящее резервирование ...............................................................................		23
2.2	Примеры решения задач ........................................................................................	24
2.3	Задачи для самостоятельного решения ................................................................	35
Библиографический список..........................................................................................		37

1 РАСЧЁТ ПОКАЗАТЕЛЕЙ НАДЁЖНОСТИ НЕРЕЗЕРВИРОВАННЫХ НЕВОССТАНАВЛИВАЕМЫХ СИСТЕМ

1.1 Методы расчёта показателей надёжности

Критериями надёжности невосстанавливаемых систем являются:

1)Pc (t) – вероятность безотказной работы системы в течение времени t;

2)Tc – среднее время безотказной работы системы;

3)λc (t) – интенсивность отказа системы в момент времени t;

4)fc (t) – плотность распределения времени до отказа.

Между этими показателями существуют следующие зависимости:

∫λc ( t )dt

Pc (t) = e 0

T1c = ∫∞ Pc (t)dt

λc (t)

fc (t) = Qc'

Pc (t) = 1

	=	fc (t)
	=	P (t)
		P (t)
		c

(t) = −Pc' (t)

− ∫t fc (t)dt

Замечание: следует иметь в виду, что среднее время безотказной работы является неудовлетворительным показателем надёжности систем с коротким временем работы.

Структурная схема нерезервированной системы, состоящей из n элементов, приведена на рисунке 1.1.

1		2		…		n

Рисунок 1.1 – Структурная схема нерезервированной системы При отказе любого элемента наступает отказ системы. При этом остальные

элементы системы прекращают свою работу.

Показатели надёжности такой системы вычисляются по формулам:

Pc (t) = Пj =1 Pj (t)

T1c = ∫∞ Pc (t)dt

λc (t) = ∑n λj (t)

j =1

fc (t) = f1 (t)P2 (t)...Pn (t) + P1 (t) f2 (t)...Pn (t) + ... + P1 (t)P2 (t)... fn (t) ,

где Pj(t) – вероятность безотказной работы j-го элемента, j = 1,2, …, n;

fj (t) – плотность распределения времени до отказа j-го элемента, j = 1,2, …,n; λj (t) – интенсивность отказа j-го элемента, j = 1,2, …, n.

Для случая постоянных интенсивностей отказов элементов имеют место соотношения:

P (t) = e−λc t
c
λc = ∑n λj
	j=1
T	=	1

1c		λ	c

fc (t) = λc e −λc t

1.2 Примеры решения задач

Пример 1.1. Нерезервированная система состоит из 5 элементов. Интенсивности их отказов приведены в таблице 1.1.

Таблица 1.1 – Интенсивности отказов элементов

Номер элемента	1	2	3	4	5
λi, час-1	0,00007	0,00005	0,00004	0,00006	0,00004

Определить показатели надёжности системы: интенсивность отказа, среднее время безотказной работы, вероятность безотказной работы, плотность распределения времени безотказной работы. Показатели надёжности P(t) и f(t) получить на интервале от 0 до 1000 часов с шагом 100 часов.

Решение. Вычислим интенсивность отказа и среднее время безотказной работы системы:

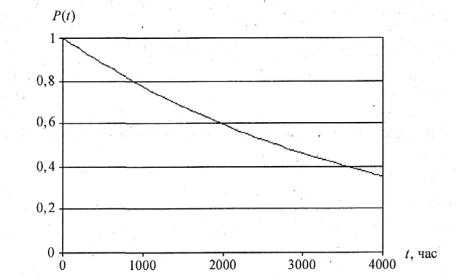
Получим значения вероятности безотказной работы и плотности распределения времени до отказа, табулируя функции на интервале от 0 до 1000 часов.

Pc (t) = e −λc t = e −0,00026 t и fc (t) = λc e −λc t = 0,00026e −0,00026 t

Результаты табулирования представлены в таблице 1.2.

Таблица 1.2 – Вероятность безотказной работы и плотность распределения времени до отказа

t, час	Pc (t)	fc (t)
0	1	0,00026
100	0,974335	0,000253
200	0,949329	0,000247
300	0,924964	0,000240
400	0,901225	0,000234
500	0,878095	0,000228
600	0,855559	0,000222
700	0,833601	0,000217
800	0,812207	0,000211
900	0,791362	0,000206
1000	0,771052	0,000200

Графическая иллюстрация Pc(t) и fc(t) показана на рисунках 1.2 и 1.3.

Рисунок 1.2 – Вероятность безотказной работы системы

Рисунок 1.3 – Плотность распределения времени до отказа

Интенсивность отказа системы в данном случае есть величина постоянная, равная λс=0,00026 час-1, её графиком является прямая, параллельная оси времени.

Пример 1.2. Нерезервированная система состоит из 5 элементов, имеющих различные законы распределения времени работы до отказа. Виды законов распределения и их параметры приведены в таблице 1.3.

Таблица 1.3 – Законы распределения времени до отказа

Номер	1	2	3	4	5
элемента	1	2	3	4	5
элемента
Закон
распределения	W(2; 1800)	Г(7; 300)	R(8·10-8)	Exp(0,002)	TN(2000; 90)
времени до
отказа

Втаблице 1.3 и в дальнейшем приняты следующие обозначения законов распределения:

W – Вейбулла; Г – гамма;

R – Рэлея;

Exp – экспоненциальный; TN – усечённый нормальный; N – нормальный;

U – равномерный.

Вскобках указаны параметры распределений.

Определить показатели надёжности каждого элемента и всей системы: вероятность безотказной работы; среднее время безотказной работы; интенсивность отказа, плотность распределения времени безотказной работы. Для показателей, зависящих от времени, получить решение в виде таблиц и графиков.

Решение: в таблице 1.3 заданы параметры законов распределения времени до отказа. Вычислим начальные моменты распределений: математические ожидания и средние квадратические отклонения. Для этого воспользуемся формулами связи моментов с параметрами распределений, которые приведены в таблице 1.4.

Таблица 1.4 – Связь параметров распределений с первыми двумя моментами

Распределение		m		σ
Экспоненциальное Exp(λ)		1		1
		λ		λ

Равномерное U(a, b), a≥0	a + b		b − a
	2		2	3

Гамма Г(α, β)	α·β		α β

σ0 1 + k m0 − k 2

σ0

−

m 02

Усечённое нормальное

m0 +k σ0

k =

2σ 02

2π

TN(m0, σ0)

c =

+Ф

0,5

Рэлея R(λ)

4 −π

4λ

Вейбулла W(α, β)

βГ(1 +1 / α)

Г (1 + 2 / α) − Г2 (1 +1 / α)

Нормальное N (m, σ) m>3·σ

В таблице введены следующие обозначения:

x 2

Ф0

(t) =

∫e −

dx – функция Лапласа;

2π

Г(α) = ∫∞ xα−1 e −x dx – гамма – функция.

Определим математическое ожидание и среднее квадратическое отклонение времени до отказа элементов.

Элемент 1. Распределение Вейбулла с параметром формы α = 2 и параметром масштаба β = 1800:

m=1800·Г(1,5)=1595 час, σ = 1800

Г(2) − Г2 (1,5) =834 час.

Элемент 2. Гамма – распределение с параметром формы α = 7 и параметром

масштаба β = 300:

m=7·300 =2100 час, σ =

7 300 =794 час.

Элемент 3. Распределение Рэлея с параметром λ=8·10-8:

m =

= 3133 час, σ =

4 −π

= 1638 час.

4 8 10−

4 8 10−8

Элемент 4. Экспоненциальное распределение с параметром λ=0,0002:

m =

= 5000 час, σ = m = 5000 час.

0,0002

Элемент 5. Усечённое нормальное распределение с параметрами m0 = 2000,

σ0 = 900:

−

m02

20002

k =

2σ02

e −

= 0,0342

2 9002

2000

2π 0,5

+Ф

2π 0,5 +Ф0

σ0

900

Значит,

m = 2000 +0,0342 900 = 2029 час,

σ = 900 1 + 0,0342 2000900 − 0,03422 = 931 час.

Полученные значения сведены в таблицу 1.5.

Таблица 1.5 – Параметры законов распределения времени до отказа элементов

Номер элемента	1	2	3	4	5
Среднее время безотказной работы, час.	1595	2100	3133	5000	2029
Среднее квадратическое отклонение времени безотказной	834	794	1638	5000	931
работы, час

Для вычисления вероятности безотказной работы и плотности распределения времени до отказа элементов нам потребуются аналитические выражения, которые приведены в таблице 1.6.

В гамма–распределении

функция

I(α, t) =

∫t

xα−1 e −x dx есть

неполная

Г(α)

гамма – функция.

Таблица 1.6 – Некоторые законы распределения вероятностей

Распределение

f(t)

P(t)

Экспоненциальное Exp(λ)

λ·e-λt

e-λt

, a ≤ t ≤ b

t<a;

b − t

b − a

a ≤t ≤ b;

Равномерное U(a, b), a≥0

b − a ,

0, t<a, t>b

t>b

t α−1

−

1 − I

Гамма Г(α, β)

α,

βα Г(α)

−

( t −m0 )2

2σ02

Усечённое нормальное

σ0

2π e

− m

TN (m

, σ

)

0,5

−Ф

C =

m≥1,33σ

0,5 +Ф0

σ0

Рэлея R(λ)

2 λ t e −λt 2

e−λt 2

α t

α−1

−

Вейбулла W(α, β)

βα

t − m

−

( t

−m )2

0,5 −Ф0

Нормальное N (m, σ), m>3σ

2σ

2π

Равномерное и нормальное распределения имеют ограничения на параметры для того, чтобы их можно было использовать для решения задач надёжности в неотрицательной временной области (t≥0).

Вычислим вероятность безотказной работы элементов. Элемент 1. Распределение Вейбулла:

		t α			t	2
				−

P (t) = e	−		= e		1800
P (t) = e		β	= e		1800
1

Элемент 2. Гамма-распределение:

∞

xα−1

−

P2 (t) = ∫

e dx = 1

− I α,

= 1

− I 7,

300

Г(α)

1 / 41 2 3 4 > Следующая >>>

Соседние файлы в папке Надежность_1

#
09.06.20151.87 Mб132poz115.pdf
#
09.06.20155.59 Mб192uprresurs.doc
#
09.06.201522.02 Кб100Восстанавливаемыми называют такие объекты.doc
#
09.06.2015433.15 Кб318Министерство транспорта Российской Федерации.doc
#
09.06.20151.35 Mб167Расчет показателей надежности невосстанавливаемых нерезервированных систем.doc
#
09.06.201524.58 Кб150Расчет показателей надежности.doc