4. Расчет задач по определению показателей надежности восстанавливаемых элементов систем электроснабжения

Задача 4.1.

Система состоит из трех элементов с основным соединением, характеризующимися постоянными интенсивностями отказов и восстановлений:

1/час; 1/час; 1/час;

1/час; 1/час; 1/час.

Определить значения коэффициента готовности К_г и функции готовности G(t) для момента времени 0,5 часа.

Решение:

Коэффициент готовности определяется по формуле [1,2,5]:

 

,                                            (4.1)

 

где – результирующее значение интенсивности восстановления системы, 1/час; – результирующее значение интенсивности отказов системы, 1/час.

Результирующее значение интенсивности отказов системы определим по (2.5):

1/час;

 

Результирующее значение интенсивности восстановлений системы определим по следующему выражению из [1,2,5]:

 

1/час;                                           (4.2)

1/час;

 

Определим значение коэффициента готовности по (4.1):

 

.

 

Значение функции готовности определяется по формуле в соответствии с [1,2,5]:

,                               (4.3)

.

 

Функция готовности показывает вероятность, с которой система к моменту времени t будет находится в работоспособном состоянии.

 

5. Расчет задач по определению показателей надежности при использовании критериев сходимости

Задача 5.1.

В сложной электронной системе с экспоненциальным законом возникновения отказов за 2000 часов работы зафиксировано 12 отказов. Определить границы истинной средней наработки до отказа системы при коэффициенте доверия . Больше никаких данных нет.

Решение:

Средняя наработка до отказа лежит в пределах:

 

;                                         (5.1)

 

В соответствии с [1,3] по имеющимся исходным данным можно определить средневзвешенное значение средней наработки до отказа по результатам наблюдений:

,                                               (5.2)

 

где t_набл – период наблюдений, час.; n – число отказов за период наблюдений.

С учетом результатов наблюдений получим:

 

час;

 

При использовании критерия согласия Пирсона доверительный интервал для средней наработки до отказа при равных вероятностях выхода за правую (верхнюю) и левую (нижнюю) границы для экспоненциального распределения [1,3] определяется по выражению:

 

,                                  (5.3)

 

где 2n – число степеней свободы; – уровень значимости; n – количество опытных данных.

Уровень значимости определяется по выражению [1,3]:

 

;                                                  (5.4)

 

Из исходных данных имеем:

;

2n=24;

 

По таблице кванителей распределения [1,3] определяем верхний и нижний пределы доверительного интервала:

 

 

Тогда значения верхней и нижней границы средней наработки до отказа в соответствии с (5.3):

 

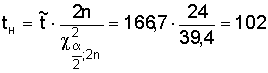час;

час;

 

Таким образом, истинное значение средней наработки до отказа лежит в пределах от 102 до 323 часа с вероятностью 0,95.

 

 

Список литературы

1.Анищенко, В.А. Надежность систем электроснабжения : учеб. пособие / В.А. Анищенко. – Минск : УП “Технопринт”, 2001. – 160 с.

2.Балабанов, В.Н. Надежность электроустановок : учебно-методи­чес­кое пособие / В.Н. Балабанов. – Хабаровск : ДВГУПС. 1999 – 97 с.

3.Ефимов, А.В. Надежность и диагностика систем электроснабжения железных дорог / А.В. Ефимов, А.Г. Галкин. – М. : УМК МПС России, 2000.

4.Сердинов, С.М. Повышение надежности устройств электроснабжения электрифицированных железных дорог / С.М. Сердинов. – М. : Транспорт, 1985.

5. Колявин, В.П. Надежность и диагностика электроустановок : учеб. пособие / В