Угол |
наклона |
|
нулевой |
линии α0 31o. Эпюра σ дана на рис. 2.4. |
||||||||||||||||||||||||||
Напряжения в опасных точках сечения |
|
|||||||||||||||||||||||||||||
max σ = ± |
9 |
3,214 10 |
2 |
|
0,857 |
|
=1,199 кН/см2 |
12МПа. |
||||||||||||||||||||||
|
153 |
|
|
1+1,5 |
3,214 |
|
||||||||||||||||||||||||
min |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
KR |
|
|
|
MY |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Эп. σ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
(MПа) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α0=31° |
||
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|||||||
|
|
|
|
|
|
|
|
|
я |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
MX |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
л |
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
KS |
||||
|
|
|
у |
е |
|
|
я |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Н |
|
н |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
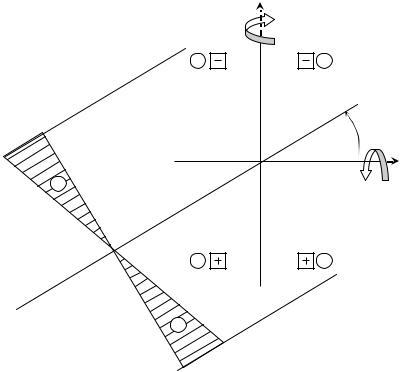
Рис. 2.4. Эпюра нормальных напряжений σ и положение нулевой линии
2.2. Задача 13. Сложное сопротивление жесткого бруса
Основные понятия
В случае совместного действия на балку косого изгиба и осевого растяжения или сжатия в соответствии с принципом независимости действия сил нормальные напряжения в произвольной точке поперечного сечения с координатами (x, y) определяют по формуле
σ = σ |
N |
+ σ |
Mx |
+ σ |
My |
= |
N |
+ |
M |
x |
y + |
My |
x . |
|
|
|
|
||||||||||
|
|
|
|
A |
|
Jx |
Jy |
|
|||||
|
|
|
|
|
|
|
|
|
|||||
Для стержней из материалов, одинаково работающих на растяжение и сжатие с поперечными сечениями, имеющими угловые точки, равноудаленные от главных осей (например, прямоугольник, двутавр), условие прочности имеет вид
22
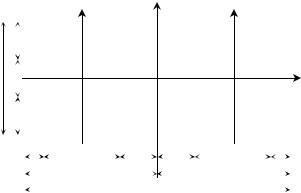
max σ = |
N |
+ |
|
M |
x |
+ |
My |
m [σ]. |
A |
|
|
|
Wy |
||||
|
|
Wx |
|
|||||
Нулевая линия при действии изгиба с растяжением или сжатием не проходит через центр тяжести поперечного сечения. Абсолютные величины отрезков ax и ay, отсекаемых нулевой линией на осях координат, определяются из выражений:
|
N Jy |
|
|
N |
2 |
|
|
|
|||
|
|
|
|
||||||||
ax = |
|
|
|
= |
|
|
|
iy |
|
|
; |
My |
|
A |
My |
|
|||||||
|
|
|
|
|
|
|
|
|
|||
|
N Jx |
|
|
N |
|
|
|
|
|
||
|
|
|
|
|
|
||||||
|
|
|
2 |
|
|
|
|||||
ay = |
|
|
|
= |
|
|
|
ix |
, |
||
Mx |
|
A |
Mx |
||||||||
|
|
|
|
|
|
|
|
|
|||
где ix и iy – главные радиусы инерции сечения.
В случае, когда параллельная оси стержня нагрузка приложена внецентренно (с эксцентриситетом), возникает внецентренное растяжение (сжатие). Внутренние усилия:
N = F; Mx = FyF; My = FxF,
где F – величина приложенной силы; yF и xF – координаты точки приложения нагрузки. Напряжения в произвольной точке сечения вычисляются по
формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xF |
|
yF |
|
|
|
|
σ = |
N |
1 |
+ |
x + |
y |
|
. |
|||
|
2 |
2 |
|
|||||||
|
|
|
|
|
|
|||||
|
A |
|
|
iy |
|
ix |
|
|
|
Выпуклая область вокруг центра тяжести сечения, внутри которой приложение силы F вызывает во всех точках поперечного сечения напряжения одного знака, называется ядром сечения. Для построения ядра сечения необходимо задаться различными положениями нулевой линии, проводя ее касательно к контуру и нигде не пересекая его, и вычислить координаты соответствующих точек приложения силы по формулам:
|
i2 |
iy2 |
||
y я = − |
x |
; xя = − |
|
. |
|
|
|||
|
ay |
ax |
||
Вычисленные точки определяют контур ядра сечения.
Условие примера
Для бруса определить грузоподъемность [F] при К1 = 0,5; К2 = 2;
[σ]=20 МПа = 2 кН/см2 из условия
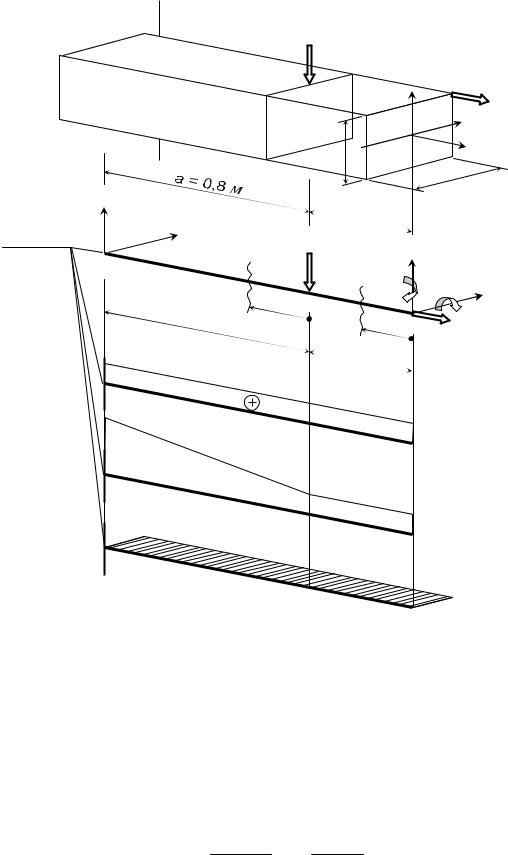
прочности по нормальным напряжениям. Схема поперечного сечения показана на рис. 2.5. Схема бруса и нагрузки дана на рис. 2.6.
|
|
|
|
|
Y1 |
|
YC |
|
Y2 |
||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 5 |
|
|
C1 |
|
|
C |
C2 |
|
|
XC |
|||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
5 |
5 |
|
10 |
|
2,5 |
|
|
|
|
|
|
2,5 |
|
|
|
|
|||||
|
|
|
|
|
17,5 |
|
|
35 |
|
17,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.5. Поперечное сечение (размеры указаны в сантиметрах)
23
a
консоль
бyC
Опасное |
|
xC |
|
||
сечение |
|
A0 |
|
|
|
|
|
|
8 |
0 |
c |
|
||
|
|
м |
вЭп. N 2F
[кН]
55F
Эп. MX
[кНм]
Эп. MY |
35F |
[кНм] |
|
F1=K1F=0,5F
|
yC |
|
|
F2=K2F=2F |
|
|
|
|
|
см |
|
|
|
xC |
C |
|
|
zС |
|
=15H |
|
|
||
|
|
5 |
м |
|
|
|
|
с |
|
|
|
3 |
|
|
|
= |
|
|
|
|
B |
|
|
|
|
b = 0, |
|
|
|
|
4 м |
|
|
0,5F |
yC mY=35F |
|
|
|
||
z |
S |
|
xC |
|
mX=15F |
||
2 |
z |
||
|
|
||
|
|
L 2F |
|
|
40 |
1 |
|
|
c |
|
|
|
|
м |
|
2F
15F
15F
35F
Рис. 2.6. Сложное сопротивление жесткого бруса: а – заданная система; б – приведение сил к главным осям; в – эпюры внутренний усилий
Расчет
1. Геометрические характеристики сечения.
В силу симметрии сечения оси xCCyC – главные.
Площадь A = 35 15 − 2 10 5 = 425 см2.
Главные центральные моменты инерции:
JxC = 3512153 − 2 101253 = 9635 см4;
24
|
|
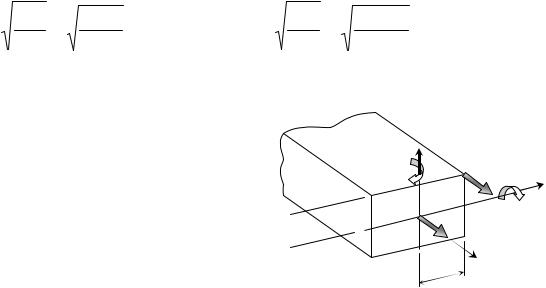
35 |
3 |
15 |
|
10 |
3 |
5 |
|
2 |
|
|
4 |
JyC |
= |
|
|
|
+10 |
5 10 |
|
||||||
12 |
− 2 |
12 |
|
|
= 42760 см . |
||||||||
|
|
|
|
|
|
|
|
||||||
Моменты сопротивления:
|
|
|
Jx |
|
9635 |
3 |
||
|
|
|
C |
|
|
|||
Wx |
= |
|
|
|
= |
7,5 |
=1285 см ; |
|
|
ymax |
|||||||
C |
|
|
|
|
||||
|
|
|
|
|
|
|
||
|
|
|
JyC |
|
42760 |
3 |
||
WyC |
= |
|
|
|
= |
17,5 |
= 2443 см . |
|
xmax |
||||||||
|
|
|
|
|||||
Радиусы инерции:
ix = |
Jx |
= |
9635 |
= 4,76 см; iy = |
Jy |
|
= |
42760 |
=10,03 см. |
C |
425 |
|
C |
425 |
|||||
C |
A |
|
C |
A |
|
|
|||
|
|
|
|
|
|
|
|
||
Квадраты радиусов инерции:
ix2C = 4,762 = 22,66 см2; iy2C =10,032 =100,6 см2.
2. Приведение внешних сил к главным осям торцового сечения консоли
(рис. 2.7).
Перенося силу F2 = 2F к центру С
ymax
xmax = 17,5 см |
|
ymax = 7,5 см |
|
yC |
|
my=35F |
F2 = 2F |
|
xC |
С |
mx=15F |
|
|
2F |
zC |
x |
|
xma |
|
сечения, получаем эквивалентную систему нагрузок на торце консоли, включающую силу 2F и моменты относительно осей xC и yC :
Рис. 2.7. Приведение нагрузки к главным осям торцевого сечения
mx = 2Fymax = 2F 7,5 =15F кНсм; my = 2Fxmax = 2F 17,5 = 35F кНсм.
3. Построение эпюр усилий (рис. 2.6, в). Участок SL.
N = 2F = const – растяжение;
Mx = mx =15F кНсм = const – растянуты верхние волокна; My = my = 35F кНсм = const – растянуты правые волокна.
Участок А0S.
N = 2F = const – растяжение;
Mx = mx + F1z2 =15F + 0,5F z2 – растянуты верхние волокна;
25
yC
f
MY M xC
С N X
сечение A0
Рис. 2.8. Определение опасной точки в опасном сечении
Mx (0) =15F кНсм;
Mx (80) =15F + 0,5F 80 = 55F кНсм;
My = my = 35F кНсм = const – растянуты
правые волокна.
4. Условие прочности для опасной точки опасного сечения A0.
В угловых точках показаны знаки нормальных напряжений от N ( ), MX ( ), MY (U). Опасной является точка f (рис. 14).
Условие прочности для опасной точки f имеет вид
max σf = |
N |
+ |
|
M |
x |
+ |
|
My |
m [σ]. (4.1) |
|
A |
WxC |
WyC |
||||||||
|
|
|
|
|||||||
При подстановке в условие прочности внутренних усилий в опасном се-
чении N = 2F, MX = 55F, MY = 35F получим |
425 2 |
|
|
|
|||||||||||||||
[F] m |
|
|
|
A[σ] |
|
|
= |
|
|
|
|
|
= 32,3 кН. |
||||||
|
|
|
55A |
|
35A |
|
|
|
55 |
425 |
|
35 425 |
|
||||||
2 |
1 |
+ |
+ |
|
2 1 |
+ |
|
|
+ |
|
|
||||||||
2 1285 |
2 2443 |
||||||||||||||||||
2W |
|
|
2W |
||||||||||||||||
|
|
|
|
XC |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
YC |
|
|
|
|
|
|
|
|
|
||||
Итак, допускаемая |
|
грузоподъемность |
соответствует нагрузке |
||||||||||||||||
F1 = 0,5F = 16,15 кН, F2 = 2F = 64,6 кН.
5. Построение ядра сечения (рис. 2.9).
Координаты угловых точек ядра в осях xCСyC вычисляются по формулам:
|
iy2 |
|
ix2 |
|
||
xя = − |
C |
; |
y я = − |
C |
, |
(2.6) |
|
|
|||||
|
ax |
|
ay |
|
||
|
|
III |
|
|
|
|
yC |
|
I |
||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
II |
|
|
|
|
|
|
|
|
II |
||||
7,5 |
|
|
|
2 |
|
|
|
|
|
|
|||
|
|
3,02 |
|
|
|
||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
3 3,02 |
|
|
xC |
||
7,5 |
|
|
|
|
4 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
IV |
|
|
|
5,74 |
5,74 |
|
|
|
IV |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
III |
17,5 |
|
|
17,5 |
|
I |
|||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|||||||||
Рис. 2.9. Ядро сечения (размеры указаны в сантиметрах)
т. 2 (x2 = 0; y2 = + 3,02 см); т. 3 (x3 = + 5,74 см; y3 = 0); т. 4 (x4 = 0; y4 = – 3,02 см).
26
где aX, aY – отрезки, отсекаемые на главных осях касательными к контуру сечения нулевыми линиями I, II, III, IV, откуда получим координаты точек 1, 2, 3, 4. Например, задав нулевую линию I–I, имеем aX = +17,5 см, aY = ×, так что координаты точки
1 |
x1 = − |
100,6 |
= −5,74 |
см; |
||
|
17,5 |
|||||
|
22,66 |
|
|
|||
y1 = − |
|
= 0 и т. д. Координа- |
||||
∞ |
|
|||||
ты точек: