
Задача 5
Выборочная зависимость между величиной основных производственных фондов Х и суточной выработкой продукции У по данным пяти независимых наблюдений представлена в таблице.
Требуется
составить выборочное уравнение линейной
парной регрессии У
на Х,
вычислить коэффициент корреляции r
между Х
и У,
на уровне значимости
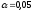 проверить значимость коэффициента
корреляции и уравнения регрессии.
проверить значимость коэффициента
корреляции и уравнения регрессии.
Таблица 8
|
i |
1 |
2 |
3 |
4 |
5 |
|
хi |
1,20 |
1,50 |
2,50 |
3,00 |
4,50 |
|
уi |
1,35 |
1,40 |
1,50 |
1,65 |
1,70 |
Решение:
Составим расчетную таблицу задачи:
Таблица 9
|
i |
xi |
xi2 |
yi |
уi2 |
xiyi |
|
1 |
1,20 |
1,44 |
1,35 |
1,823 |
1,62 |
|
2 |
1,50 |
2,25 |
1,40 |
1,960 |
2,10 |
|
3 |
2,50 |
6,25 |
1,50 |
2,250 |
3,75 |
|
4 |
3,00 |
9,00 |
1,65 |
2,723 |
4,95 |
|
5 |
4,50 |
20,25 |
1,70 |
2,890 |
7,65 |
|
|
xi = 12,70 |
xi2 = 39,19 |
yi = 7,60 |
уi2 = 11,645 |
xiyi = 20,07 |
|
Среднее значение |
|
|
|
|
4,014 |
Выборочное уравнение линейной регрессии У на Х имеет вид:
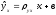 .
.
Параметры уравнения и в находятся из системы нормальных уравнений:
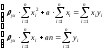
где n – объем выборки.
Согласно данным расчетной таблицы имеем:
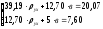
Решение этой системы вычислим по формулам:
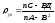 ,
,
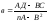 ,
,
где
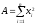 ,
,
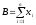 ,
,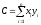 ,
,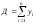 .
.
Значения А, В, С, Д указаны в расчетной таблице 9.
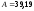 ,
,
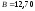 ,
,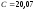 ,
,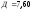 .
.
Поэтому находим:
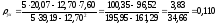 ;
;
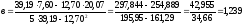 .
.
Следовательно, искомое уравнение регрессии У на Х имеет вид:
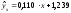 .
.
Коэффициент корреляции r между Х и У определим по формуле:
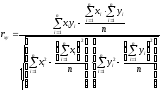

Связь между Х и У тесная, прямая.
Проверим
значимость коэффициента корреляции на
уровне значимости
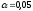 с
помощьюt
критерия Стьюдента.
с
помощьюt
критерия Стьюдента.
Найдем наблюдаемое значение критерия:
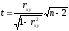
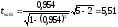 .
.
По
таблице значений t
критерия Стьюдента при уровне значимости
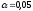 и числе степеней свободы
и числе степеней свободы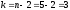 находим критическое значение:
находим критическое значение:
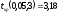 .
.
Так
как
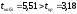 ,
то корреляцииr
является значимым.
,
то корреляцииr
является значимым.
Значимость уравнения регрессии в целом проверим с помощью F критерия Фишера:
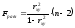 .
.
Находим наблюдаемое значение:
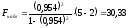
По
таблице критических точек распределения
F
Фишера находим значение
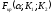 ,
соответствующее заданному уровню
значимости
,
соответствующее заданному уровню
значимости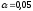 и значениям степеней свободы
и значениям степеней свободы и
и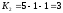 :
: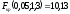 .
.
Так
как
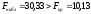 ,
то уравнение регрессии является
статистически значимым.
,
то уравнение регрессии является
статистически значимым.
Задача 6
Имеются
данные (условные) о сменной добыче угля
У
(т) и уровне механизации Х
(%), характеризующие процесс добычи угля
в семи шахтах. Установлено, что между
переменными Х
и У
существует степенная зависимость:
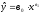 .
Требуется найти параметры этой
зависимости.
.
Требуется найти параметры этой
зависимости.
Таблица 10
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
хi |
3,2 |
3,4 |
4,1 |
4,5 |
4,9 |
5,2 |
5,8 |
|
уi |
8,5 |
8,8 |
10,2 |
12,5 |
13,4 |
15,2 |
16,8 |
Решение:
Нелинейное
уравнение регрессии
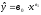 приведем к линейному, прологарифмировав
обе его части:
приведем к линейному, прологарифмировав
обе его части:
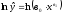 ;
;
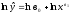 ;
;
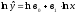 .
.
Для определения значений неизвестных параметров в0 и в1 используем метод наименьших квадратов, согласно которому должна быть составлена система нормальных уравнений и найдено ее решение:
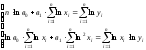
Для расчета необходимых сумм составим расчетную таблицу 11.
Таблица 11
|
i |
xi |
yi |
ln xi |
ln yi |
ln2 xi |
ln xi · ln yi |
|
1 |
3,2 |
8,5 |
1,163 |
2,140 |
1,353 |
2,489 |
|
2 |
3,4 |
8,8 |
1,224 |
2,175 |
1,498 |
2,661 |
|
3 |
4,1 |
10,2 |
1,411 |
2,322 |
1,991 |
3,277 |
|
4 |
4,5 |
12,5 |
1,504 |
2,526 |
2,262 |
3,799 |
|
5 |
4,9 |
13,4 |
1,589 |
2,595 |
2,526 |
4,124 |
|
6 |
5,2 |
15,2 |
1,649 |
2,721 |
2,718 |
4,486 |
|
7 |
5,8 |
16,8 |
1,758 |
2,821 |
3,090 |
4,960 |
|
|
31,1 |
85,4 |
10,298 |
17,301 |
15,437 |
25,797 |
Теперь, используя данные расчетной таблицы 11, составим систему нормальных уравнений:
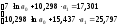
и найдем ее решение по формулам Крамера.
Имеем:
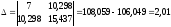 ,
,
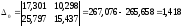 ,
,
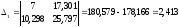 .
.
Следовательно:
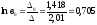 ,
,
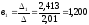 .
.
Найдем
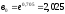 .
.
Таким образом, окончательно получаем:
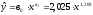 .
.

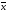 =
2,54
=
2,54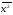 =
7,838
=
7,838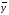 =
1,52
=
1,52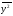 =
2,329
=
2,329