
Содержание
Задача 1 3
Задача 2 8
Задача 3 10
Задача 4 11
Задача 5 15
Задача 6 18
Задача 7 20
Список использованной литературы 22
Задача 1
Выборка случайной величины Х задана интервальным вариационным рядом (Ii – i-ый интервал, ni – частота).
Таблица 1
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Ii |
2 – 6 |
6 – 10 |
10 – 14 |
14 – 18 |
18 – 22 |
22 – 26 |
26 – 30 |
|
ni |
9 |
16 |
20 |
26 |
18 |
6 |
5 |
Найти:
1. относительные частоты (частости) Wi;
2. накопленные частоты niнак;
3. накопленные частости Wiнак.
Вычислить:
1.
выборочную среднюю
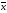 ;
;
2. смещенную оценку дисперсии Д;
3. несмещенную оценку дисперсии S2;
4. среднее квадратическое отклонение ;
5. коэффициент вариации v.
Построить:
1. гистограмму частот;
2. эмпирическую функцию распределения;
3. кумулятивную кривую.
Указать:
1. моду Мо;
2. медиану Ме.
Решение:
Вычисляем объем выборки:
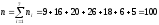 .
.
Относительные частоты вычисляются по формуле:
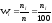 .
.
Получим:
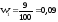 ,
,
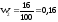 ,
,
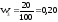 ,
,
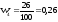 ,
,
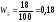 ,
,
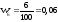 ,
,
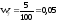 .
.
Дальнейшие расчеты оформим в виде сгруппированного ряда:
Таблица 2
|
i |
Ii |
ni |
Wi |
niнак |
Wiнак |
|
1 |
2 – 6 |
9 |
0,09 |
9 |
0,09 |
|
2 |
6 – 10 |
16 |
0,16 |
25 |
0,25 |
|
3 |
10 – 14 |
20 |
0,20 |
45 |
0,45 |
|
4 |
14 – 18 |
26 |
0,26 |
71 |
0,71 |
|
5 |
18 – 22 |
18 |
0,18 |
89 |
0,89 |
|
6 |
22 – 26 |
6 |
0,06 |
95 |
0,95 |
|
7 |
26 – 30 |
5 |
0,05 |
100 |
1 |
|
|
- |
100 |
1 |
- |
- |
Смещенная оценка Д вычисляется по формуле:
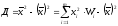 ,
,
где
xi
–
середина интервала Ii
(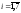 ).
).
Вычислим
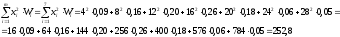
Выборочная средняя вычисляется по формуле:
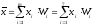 ,
,
где
xi
–
середина интервала Ii
(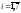 ).
).
Таким образом, находим:
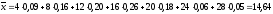 .
.
Теперь получаем:
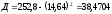 .
.
Несмещенная оценка дисперсии S2 вычисляется по формуле:
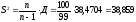 .
.
Для оценки среднего квадратического отклонения используется несмещенная дисперсия S2. Согласно определению для имеем:
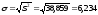 .
.
Вычисляем
значения накопленных частот
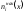 и полученные значения записываем в
таблицу 2.
и полученные значения записываем в
таблицу 2.
Согласно
определению, накопленная частота
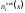 равна числу вариантов со значениемХ
меньше заданного значения х.
Так как значения Х
< 6 наблюдались 9 раз (в интервале I1),
то
равна числу вариантов со значениемХ
меньше заданного значения х.
Так как значения Х
< 6 наблюдались 9 раз (в интервале I1),
то
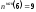 .
Это значение записываем в верхней клетке
столбца
.
Это значение записываем в верхней клетке
столбца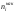 таблицы 2.
таблицы 2.
Значения
Х
< 10 наблюдались 9+16 = 25 раза (соответственно
в интервалах I1
и I2);
поэтому
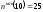 .
Аналогичным образом находим остальные
значения накопленных частот и записываем
в соответствующие клетки таблицы 2.
.
Аналогичным образом находим остальные
значения накопленных частот и записываем
в соответствующие клетки таблицы 2.
После
вычисления всех значений
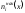 определяем значения накопленных
частостей по формуле:
определяем значения накопленных
частостей по формуле:
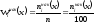 .
.
и записываем в таблицу 2.
Коэффициент вариации v определяется по формуле:
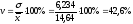 .
.
Для построения гистограммы на оси абсцисс откладываем отрезки частичных интервалов Ii варьирования и на этих отрезках как на основаниях строим прямоугольники с высотами, равными частотам соответствующих интервалов.
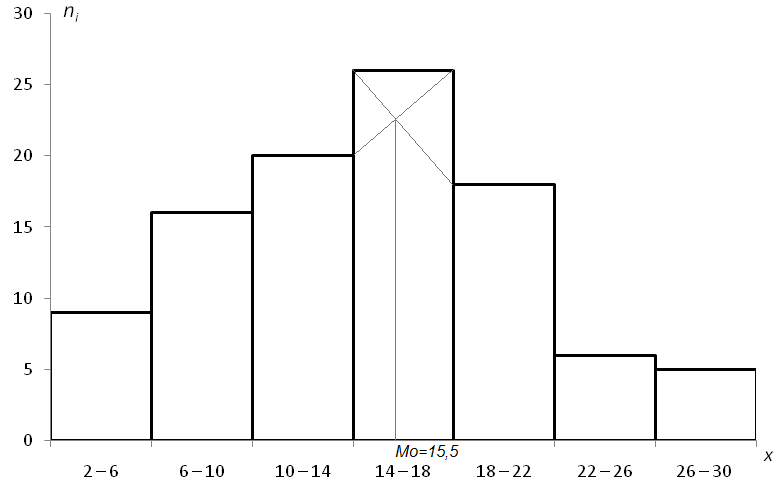
Рис.1. Гистограмма частот
С помощью гистограммы находим моду – т.е. вариант, которому соответствует наибольшая частота: Мо 15,5.
Согласно определению эмпирическая функция распределения
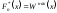
для
данного значения х
представляет накопленную частость. Для
интервального вариационного ряда (табл.
2) имеем лишь значения функции распределения
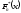 на концах интервала, указанные в правом
крайнем столбце таблицы 2. Для графического
изображения этой функции целесообразно
ее доопределить, соединив точки графика,
соответствующие концам интервалов,
отрезками прямой. Полученная таким
образом ломаная совпадает с кумулятивной
кривой (кумулятой).
на концах интервала, указанные в правом
крайнем столбце таблицы 2. Для графического
изображения этой функции целесообразно
ее доопределить, соединив точки графика,
соответствующие концам интервалов,
отрезками прямой. Полученная таким
образом ломаная совпадает с кумулятивной
кривой (кумулятой).
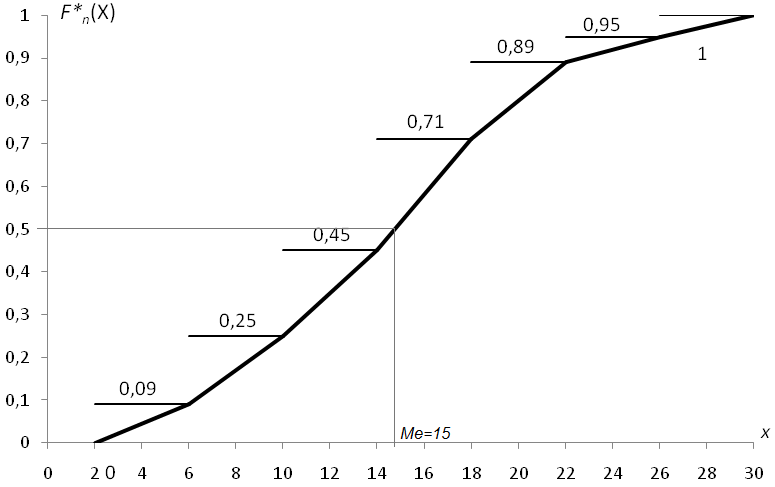
Рис.2. Кумулята
С
помощью кумуляты приближенно найдем
медиану как значение признака, для
которого
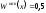 .
Очевидно,Ме
15.
.
Очевидно,Ме
15.
