Вариант № 7

1. Уравнения прямой, проходящей через точку и перпендикулярной плоскости , будут иметь вид:

2. Уравнение плоскости, проходящей через точку и параллельной плоскости

, будет иметь вид:

3. Канонические уравнения прямой, проходящей через точку и параллельной прямой, проходящей через точки, будут иметь вид:

4. Установите соответствие между уравнением плоскости и её положением в пространстве

1) а) содержит ось

2) б) параллельна оси

3) в) параллельна оси

4) г) параллельна оси

д) проходит через начало координат

5. Даны вершины треугольникаАВС. Тогда уравнение высоты, проведённой из вершиныВ, будет иметь вид:

6. Угловой коэффициент прямой будет равен:

7. Записать уравнение прямой, проходящей через две заданные точки A(5;-1) иB(3;-2).

В ответе указать абсциссу точки пересечения найденной прямой с осьюОХ.

8. Пусть - взаимно перпендикулярные вектора, длины которых равны 2 и 1 соответственно. Тогда длина векторабудет равна:

9. Модуль векторного произведения векторов иравен:

10. Угол между векторами равен:

Вариант № 8

1. Уравнение плоскости, проходящей через точку и перпендикулярной

прямой , будет иметь вид:

2. Уравнения прямой, проходящей через точки А(1;-2;1) и B(3;1;-1), имеют вид:

3. Найти абсциссу точки пересечения прямой

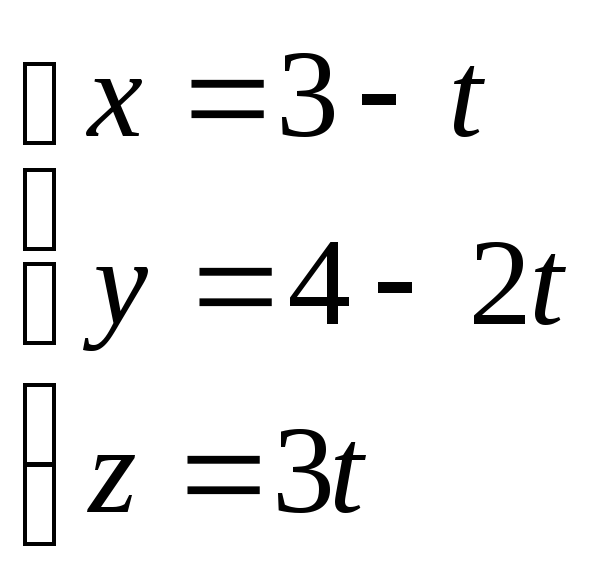с плоскостью.

4. При каком значениипрямая и плоскость

будут параллельны?

5. Записать уравнение прямой, проходящей через середину отрезка , гдеА(-3;2) ,

В(3;6) и перпендикулярной ему. В ответе указать абсциссу (х) точки пересечения найденной прямой с осьюОХ.

6. Расстояние от точки до прямойбудет равно:

7. Записать уравнение прямой, проходящей через две заданные точки A(5;-1) иB(3;-2).

В ответе указать ординату точки пересечения найденной прямой с осью.

8. Если и угол между векторамиравен, то скалярное произведение векторовравно:

9. Векторное произведение векторов иесть векторравный:

10. При каких значениях параметров иплоскостиибудут параллельны?

Вариант № 9

1. Уравнения прямой, проходящей через точку и перпендикулярной плоскости , будут иметь вид:

2. Уравнение плоскости, проходящей через точку и параллельной плоскости

, будет иметь вид:

3. Канонические уравнения прямой, проходящей через точку и параллельной прямой, проходящей через точки, будут иметь вид:

4. При каком значениипрямая и плоскость

будут перпендикулярны?

5. Даны вершины А(2;-4) ,В(1;3) ,С(4;-2) треугольникаАВС. Записать уравнение медианы, проведённой из вершиныА. В ответе указать абсциссу (х) точки пересечения этой медианы с осьюОХ.

6. Если точка принадлежит прямой, то координатабудет равна:

7. Записать уравнение прямой, проходящей через две заданные точки A(-2;4) иB(3;3).

В ответе указать абсциссу точки пересечения найденной прямой с осьюОХ.

8. Векторы и будут ортогональны, если число  равно:

9. Cумма координат векторного произведения векторов иравна:

10. В треугольнике с вершинами длина медианы, проведённая из вершины, будет равна: