Лабораторная работа 29

ИЗУЧЕНИЕ ЗАТУХАЮЩИХ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ С ПОМОЩЬЮ ОСЦИЛЛОГРАФА

Цель работы: Изучение с помощью электронного осцилло­графа электромагнитных колебаний, возникающих в колеба­тельном контуре, содержащем индуктивность, ёмкость и актив­ное сопротивление; изучение условий возникновения затухаю­щих колебаний в контуре; расчёт основных физических вели­чин, характеризующих эти колебания.

Введение

На рис. 1 изображена электрическая схема простейшего колебательного контура с сосредоточенными параметрами, со­держащего конденсатор ёмкостью С, катушку индуктивнос­ти L и активное сопротивление R.

Рис.1 Электрическая схема колебательного контура

Если в какой-либо момент времени на одну из пластин конденсатора внести электрический заряд или создать условия для возникновения в катушке э. д. с. индукции, а затем уб­рать источники возбуждения, в контуре возникнут электромагнитные колебания.

Исследуем характер колебаний в идеальном контуре (т. е. для R = 0). При максимальном заряде q₀ конденсатора. Энергия электрического поля конденсатора ёмкостью С

,

где U₀ — максимальная разность потенциалов на обкладках конденсатора.

Под действием сил электрического поля заряды начинают движение по замкнутому участку цепи, конденсатор разряжается, и в контуре возникает электрический ток

, (1)

где q(t) — заряд на обкладках конденсатора. Знак «минус» указывает на возрастание тока при убывании положительного заряда соответствующей пластины конденсатора. Энергия элек­трического поля конденсатора уменьшается, переходя в энер­гию магнитного поля катушки. Возрастание тока в катушке индуктивности приводит к появлению, в ней э. д. с. самоиндук­ции ε(t), противодействующей изменению тока,

.

Величина индуктивности L определяет инертные свойства контура. При полном разряде конденсатора его электрическое поле исчезает, а энергия электрического тока, локализованная в магнитном поле катушки, достигает наибольшего значения

,

где I₀—максимальная величина тока в контуре. С этого мо­мента ток в контуре начинает убывать, вследствие чего э. д. с. самоиндукции изменяет знак, препятствуя убыванию тока. При этом энергия магнитного поля катушки уменьшается, а энергия электрического поля конденсатора растёт, стремясь к максимальному значению, которому соответствует полная перезарядка конденсатора. В этот момент времени мгновенные значения электрического тока и энергии магнитного поля об­ращаются в нуль. Далее процесс повторяется в обратном порядке, и в контуре устанавливаются незатухающие электро­магнитные колебания (рис. 2).

Интервал времени между двумя ближайшими идентичны­ми состояниями контура называется периодом колебаний Т.

Рис. 2. Незатухающие электромагнитные колебания

Заметим, что описанные выше колебания в идеальном кон­туре происходили бы бесконечно долго лишь при отсутствии электромагнитного излучения (замкнутый колебательный кон­тур).

Если колебательный контур содержит активное сопротив­ление R, то при протекании изменяющегося тока в контуре часть суммарной энергии электрического и магнитного полей контура необратимо переходит в другие виды энергии (как и прежде не будем учитывать необратимые потери на электро­магнитное излучение). При этом уменьшаются с течением вре­мени амплитудные значения тока в контуре и разности потен­циалов на обкладках конденсатора. Колебания затухают.

Временная зависимость разности потенциалов U(t) = φ₁ – φ₂ на обклад­ках конденсатора в данной работе наблюдается на экра­не осциллографа. Получим эту зависимость теоретически, ис­пользуя закон Ома в обобщенной форме. Предположим, что параметры исследуемого контура L, С и R подобраны таким образом, что процессы в нём можно считать квазистационарными. Для мгновенных значений токов и напряжений в таком контуре закон Ома запишется в виде

. (2)

Преобразуем это уравнение, используя формулу (1) и учитывая, что q = CU. Тогда уравнение (2) примет вид

. (3)

Разделив обе части уравнения (3) на LC и введя обозна­чения

, ,

получим дифференциальное уравнение

, (4)

решение, которого даёт искомую зависимость U(t).

Следует отметить, что аналогичные дифференциальные уравнения могут быть получены для различного рода механи­ческих, электромеханических и других колебательных систем. В этих системах отсутствуют внешние вынуждающие воздействия, а силы сопротивления линейно зависят от скорости движения, при этом энергия, внесенная в систему извне, непрерывно уменьшается при колебаниях, переходя в энергию неупорядо­ченного процесса, в конечном счёте — в тепловую энергию.

Уравнение (4) есть линейное однородное дифференциаль­ное уравнение второго порядка с постоянными коэффициента­ми. Для частного случая, когда , его решение имеет вид:

, (5)

где φ₀ —начальная фаза колебаний, ω₀ — циклическая частота затухающих колебаний:

. (6)

Уравнение (5) описывает асимптотически затухающий ко­лебательный процесс (рис. 3) с периодом колебаний

Т.

Амплитудой затухающих колебаний считают величину

А, (7)

где U₀ — максимально возможное значение амплитуды.

Рис. 3. Затухающие электромагнитные колебания при .

Вообще говоря, при β ≠ 0 разность потенциалов U(t) не является строго периодической функцией времени U(t) ≠ U(t + T). Периодом колебаний в этом случае принято счи­тать минимальные промежутки времени между значениями A(t) одного знака.

Как видно из формул (5) и (7) степень затухания колеба­ний зависит от величины β, которую называют коэффициентом затухания. Из (7) следует, что коэффициент за­тухания есть физическая величина, обратная времени τ, в тече­ние которого амплитуда колебаний уменьшается в е раз:

U₀/А(τ) = е при t = τ = 1/β

Из (5) следует, что процесс затухания колебаний теоретически длится бесконечно долго. На практике процесс колебаний считается законченным при достаточном для каждого конкретного случая уменьшении ам­плитуды по сравнению с первоначальной.

Таким образом, характер колебательного процесса опреде­ляется соотношениями между электрическими параметрами контура R, L и С. Так, при β = 0 в контуре устанавливаются свободные гармонические, незатухающие колебания (рис. 2)

с периодом Т₀ =2π/ω₀ = (формула У. Томсона).

При β = ω₀ в контуре возникает апериоди­ческий процесс, так называемый критический режим, возможный при сопротивлении контура, равном критическому значению

(рис. 4).

Как было показано выше, при R < R_кр, т. е. β² < в контуре реализуется асимптотически затухающий колеба­тельный процесс (рис. 3).

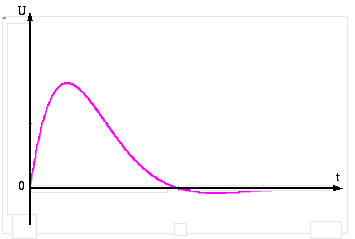
Рис. 4. Критический режим β = ω₀.

При R > R_кр , что соответствует β² > , циклическая частота и период колебаний становятся мнимыми величинами. В контуре возникает асимптотически затухающий апериодиче­ский процесс разряда конденсатора на большое активное со­противление (рис. 5). Для характеристики затухающих колебаний наряду с коэф­фициентом затухания δ приняты следующие величины: декре­мент затухания Δ, логарифмический декремент затухания Θ и добротность контураQ.

Декремент затухания Δ есть отношение амплитуд колебаний, разделенных во времени одним периодом.

В нашем случае, учитывая (7), имеем

т. е. декремент затухания является постоянной величиной, оп­ределяемой электрическими параметрами контура.

Логарифмический декремент затухания Θ вводится как натуральный логарифм декремента затухания и есть величина, обратная числу колебаний N, за которое амплитуда колебаний уменьшается в е раз

.

Добротность контура Q — важный энергетический параметр. По величине добротность равна умноженному на 2π отношению электромагнитной энергии, имеющейся в конту­ре в данный момент времени, к энергии потерянной за один период ко­лебаний, примыкающий к этому моменту, в частности, рассеян­ной на активном сопротивлении контура. Для колебаний при малых δ потери энергии на омическом сопротивлении за период в среднем равны

.

Рис. 5. Асимптотически затухающий апериодиче­ский процесс разряда конденсатора при β² > .

Тогда величина доб­ротности

.

Учитывая, что и, получим

.(8)

Для исследуемого контура при малом затухании, т. е.

, имеем , и.

Добротность в этом случае

. (9)

Физическую величину

называют волновым или характеристическим сопротивлением кон­тура.

Из соотношений (8) и (9) следует, что контур, имеющий большое активное сопротивление, обладает малой добротно­стью, т. е. интенсивно теряет электромагнитную энергию, ко­лебания быстро затухают.

Мы рассмотрели процессы, происходящие в колебательном контуре с сосредоточенными параметрами R, L и С, т. е. в идеализированном колебательном контуре. В реальных коле­бательных контурах нельзя выделить ни одного участка цепи, не обладающего активным сопротивлением, индуктивностью и ёмкостью, т. е. параметры R, L и С не являются сосредото­ченными, а распределены по участкам цепи, что усложняет анализ колебательных процессов. При расчётах необходимо также учитывать входные электрические параметры измери­тельных приборов.

Схема установки и способ возбуждения и наблюдения колебаний

На рис. 6 приведена фотография и изображена схема установки для исследования затухающих колебаний в контуре RLC.

ФПЭ-10

Генератор

Осциллограф

Магазин сопротивлений

Рис. 6. Схема установки для исследования затухающих колебаний

Для возбуждения колебаний в данной работе используется напряжение генератора прямоугольной формы, которое через конденсатор С₀ подаётся на контур для возбуждения электромаг­нитных колебаний. Величина С₀ значительно меньше ёмкости кон­тура, поэтому напряжение генератора практически полностью приложено к конденсатору С₀. Для исследуемого контура при нарастании напряжения генератора ток зарядки кон­денсаторов С можно считать постоянным. При спаде на­пряжения генератора ток разрядки конденсаторов С будет изменяться во времени. Так как в исследуемом контуре время спада напряжения генератора значительно меньше периода колебаний, изменяющийся ток разрядки конденсаторов конту­ра вызовет э.д.с. самоиндукции в катушках индуктивности, что в свою очередь, явится причиной возникновения затухающих колебаний. Эти колебания можно наблюдать на экране осцил­лографа за один период выходного напряжения генератора при соответствующем подборе частоты развёртки.

Напряжение генератора, возбуждающее контур, снима­ется непосредственно с выхода генератора, который расположенный на передней панели прибора (ЗГ, рис. 6). Исследуемая разность потенциалов U(t) с обкладок конденсатора С подается на вход «Y» осциллографа и далее че­рез усилитель поступает на вертикально отклоняющие пласти­ны осциллографа. Устойчивое изображение затухающих ко­лебаний исследуемой разности потенциалов можно получить на экране осциллографа при правильном подборе величины го­ризонтальной развёртки, частоты синхронизации и вертикаль­ного усиления.

Приборы и принадлежности. Генератор ЗГ, кассета ФПЭ-10 с колебательным кон­туром, магазин сопротивлений R_M, электронный осциллограф ОСУ-10В, сое­ди­нительные провода.