
Московский государственный университет
ПУТЕЙ СООБЩЕНИЯ (МИИТ)
Кафедра «Физика-I»
В. И. МАРЧЕНКО
ИЗУЧЕНИЕ ЯВЛЕНИЯ
ВЗАИМНОЙ ИНДУКЦИИ
Методические указания
к лабораторной работе
по дисциплине «Физика»
№244
МОСКВА – 2006
УДК 531
М - 37
Марченко В.И. Изучение явления взаимной индукции. Методические указания к лабораторной работе. – М.: МИИТ, 2006,– 13 с.
Изложена физическая суть явления взаимной индукции. Дано описание экспериментальной установки для его изучения на основе стандартного измерительного модуля ФПЭ-05, состоящего из двух аксиальных подвижных катушек, подключаемых к источнику переменного тока с регулируемыми напряжением и частотой. Соответствует программе дисциплины «Физика» (раздел «Электричество и магнетизм»). Предназначено для студентов 1 и 2 курсов энергетических, механических и строительных специальностей.
Московский государственный университет путей сообщения
( МИИТ), 2006
Московский государственный университет
ПУТЕЙ СООБЩЕНИЯ (МИИТ)
Кафедра «Физика-I»
В. И. Марченко
Утверждено
редакционно-издательским
советом университета
ИЗУЧЕНИЕ ЯВЛЕНИЯ
ВЗАИМНОЙ ИНДУКЦИИ
Методические указания к лабораторной работе по дисциплине «Физика» №244 для студентов 1 и 2 курсов энергетических, механических и строительных специальностей.
Москва – 2006
Работа № 244 «Изучение явления взаимной индукции»
Цель работы:экспериментальное изучение явления взаимной индукции двух коаксиально расположенных катушек и измерение величин коэффициентов их взаимной индуктивности при различном расположении и разных значениях частоты и амплитуды переменного тока.
П риборы
и принадлежности:
измерительный модуль ФПЭ-05 (общий вид
модуля приведен на рис.1); генератор
переменного тока звуковой частоты (PQ);
электронный осциллограф (PO);
две аксиальные катушки индуктивности
L1
и L2,
расположенные на
одной оси;
шток (Ш) с нанесенной на нем шкалой, по
которой определяется взаимное расположение
катушек.
риборы
и принадлежности:
измерительный модуль ФПЭ-05 (общий вид
модуля приведен на рис.1); генератор
переменного тока звуковой частоты (PQ);
электронный осциллограф (PO);
две аксиальные катушки индуктивности
L1
и L2,
расположенные на
одной оси;
шток (Ш) с нанесенной на нем шкалой, по
которой определяется взаимное расположение
катушек.
Рис. 1
Введение.
Я
3
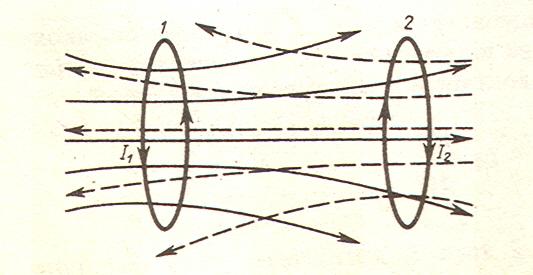
Рис. 2
Когда по одному из контуров (например, по контуру 1) протекает электрический ток I1, то в пространстве, окружающем этот ток, возбуждается магнитное поле. Индукция магнитного поля B в тех точках, где расположен контур 2, зависит от силы тока I1 и расстояния между контурами 1 и 2. Если линии индукции магнитного поля тока I1 пересекают площадь, ограниченную контуром 2, то такие контуры называются магнитосцепленными. Поток вектора B через поверхность магнитосцепленного контура 2 Φ2,1 = ∫BndS зависит от силы тока I1, протекающего в
S
контуре 1, и от площади и расположения контура 2 (под расположением контура 2 подразумевается не только расстояние между контурами 1 и 2, но и их пространственная ориентация). Теория и опыт показывают, что в неферромагнитных средах:
4
Коэффициент пропорциональности в равенстве (1) L2,1 называется коэффициентом взаимной индуктивности контуров. Он показывает, какой поток (выраженный в веберах) пронизывает данный контур при протекании в другом, магнитосцепленным с ним, контуре тока силой в 1 А. За единицу измерения коэффициента взаимной индуктивности в СИ принят генри (Гн). Взаимной индуктивностью в 1 Гн обладают такие два магнитосцепленных контура, которые отвечают следующему требованию: при протекании в одном контуре постоянного тока силой 1 А, поток вектора индукции возбужденного им магнитного поля через площадь, ограниченную вторым контуром, равен 1 Вб (1 Вб = 1 Тл∙м2).
Все приведенные выше рассуждения можно повторить для случая, когда в контуре 2 протекает ток I2, и показать, что поток вектора индукции магнитного поля тока I2 через площадь, ограниченную контуром 1, будет выражаться такой же зависимостью:
Φ1,2= L1,2∙ I2 (1`)
Согласно теореме взаимности рассматриваемого явления и предположения, что контуры размещены в неферромагнитной среде с постоянной, не зависящей от силы тока магнитной проницаемостью μ≈1, следует, что:
L2,1 =L1,2
П
5
![]()
(2)
(знак “-“ соответствует правилу, установленному Х. Ленцом для этого явления).
Одним из способов изменения магнитного потока Φ через площадь поверхности, ограниченной каким-либо из контуров, согласно (1) и (1`), является изменение силы тока в другом, магнитосцепленном с ним контуре. И тогда, если в контуре 1 произойдет изменение силы тока, то в контуре 2 будет наводиться электродвижущая сила, которая, согласно закону Фарадея (2), будет зависеть от скорости изменения тока I1:
![]()
(3)
Точно так же при изменении силы тока I2 в контуре 2 в контуре 1 будет наводиться электродвижущая сила:
![]() (4)
(4)
Таким образом, явление взаимной индукции – это явление наведения электродвижущей силы (в дальнейшем ЭДС) в контуре при изменении силы тока в другом, магнитосцепленном с ним, контуре.
