Вариант №9

Контрольная работа №1

Задачи №9, 19, 29, 39, 49, 59

Линейная и векторная алгебра. Аналитическая геометрия.

Введение в математический анализ.

Задача 1(9).

Применяя метод Гаусса исключения неизвестных, решить систему линейных уравнений. Сделать проверку найденного решения.

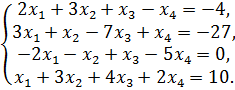
Решение:

Немного теории:

Метод Гаусса.

Метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть метода заключается в последовательном исключении неизвестных.

Рассмотрим систему линейных уравнений:

Разделим обе части 1–го уравнения на a₁₁  0, затем:

1) умножим на а₂₁ и вычтем из второго уравнения

2) умножим на а₃₁ и вычтем из третьего уравнения

и т.д.

Получим: 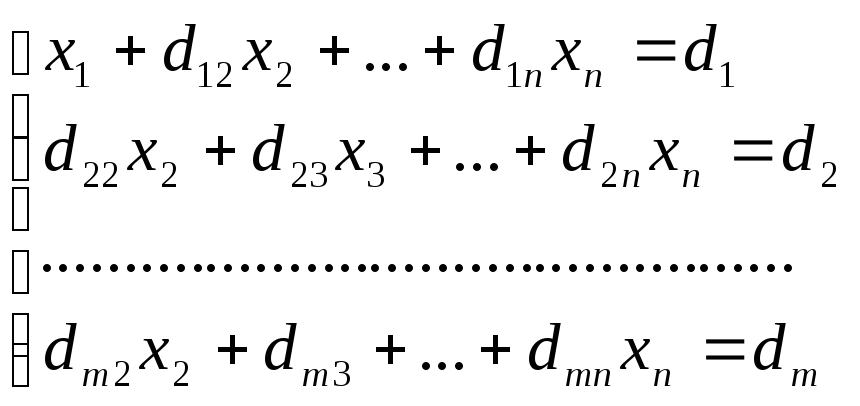, где d_1j = a_1j/a₁₁, j = 2, 3, …, n+1.

d_ij = a_ij – a_i1d_1j i = 2, 3, … , n; j = 2, 3, … , n+1.

Далее повторяем эти же действия для второго уравнения системы, потом – для третьего и т.д.

Применительно к нашей задаче:

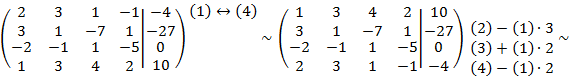
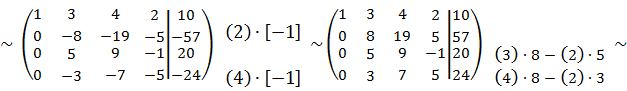
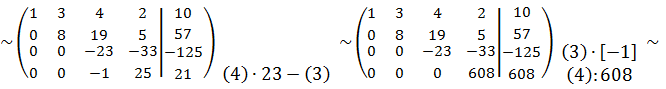
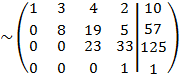
Следовательно, система примет вид:

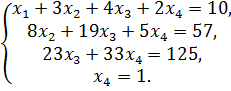
Отсюда находим все оставшиеся неизвестные:

,

,

,

,

,

,

,

,

.

Заданная система уравнений имеет единственное решение: 

, , ,

ПРОВЕРКА:

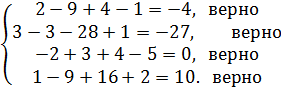
Ответ: , , ,

Задача 2(19).

Даны векторы(-2; -1; 1),(2; 3; 0),(-4; 2; 3) и (-10; -9; 3) в некотором базисе. Показать, что векторы ,иобразуют базис и найти координаты вектора в этом базисе. Систему линейных уравнений решить методом Крамера.

Решение:

Векторы образуют базис, если они линейно независимы, другими словами, если уравнения, входящие в систему:

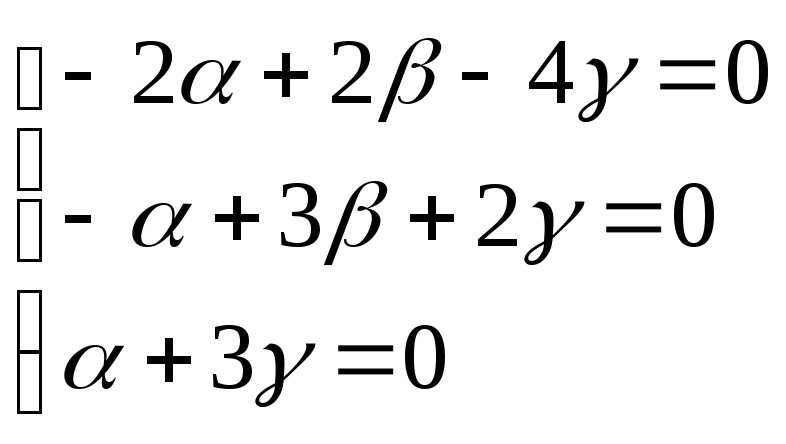линейно независимы.

Тогда .

Это условие выполняется, если определитель матрицы системы отличен от нуля.

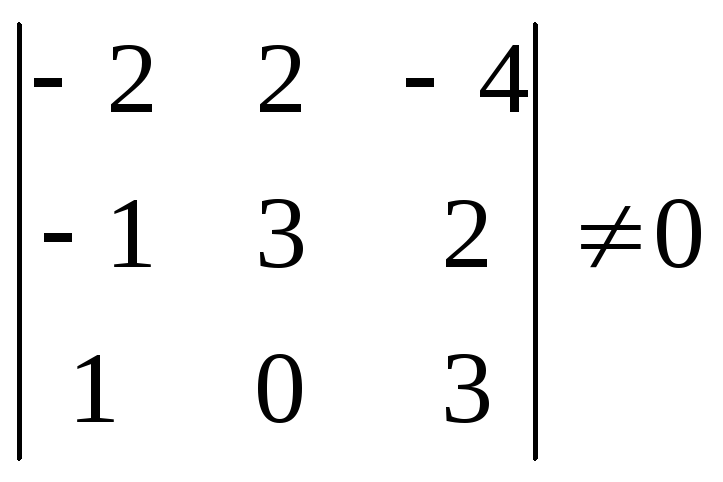
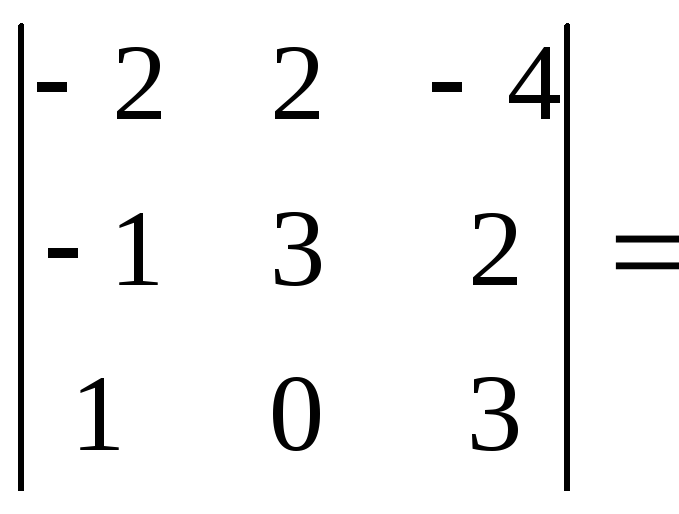
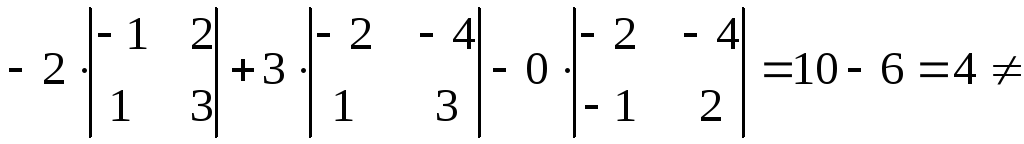0

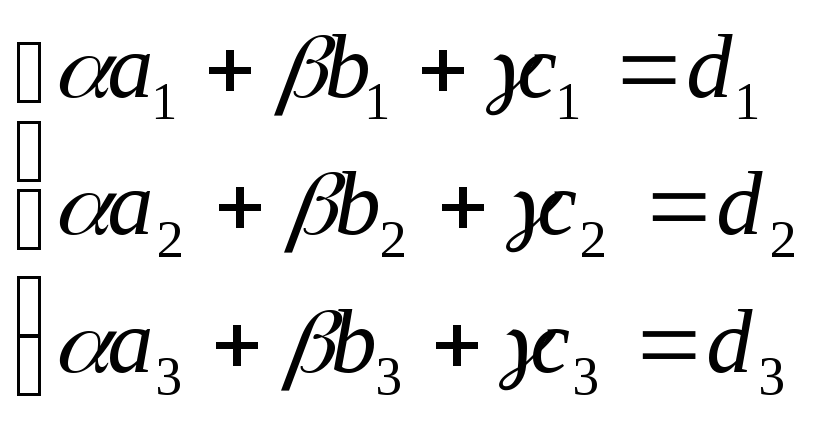Для решения этой системы воспользуемся методом Крамера.

₁ =

;

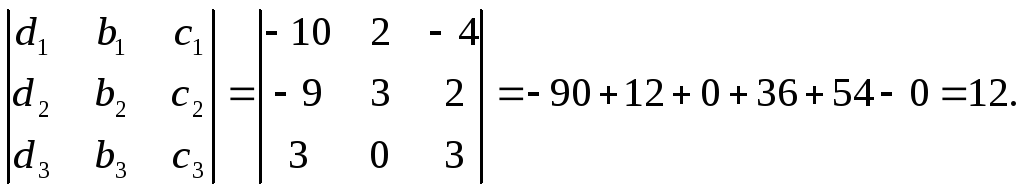
₂ =

₃ =

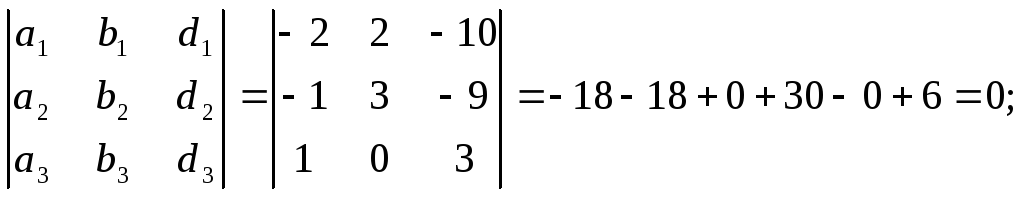
Итого, координаты вектора в базисе ,,: { 3, -2, 0}.

Ответ: { 3, -2, 0}

Задача 3(29).

Даны вершины , , , , пирамиды.

Найти:

1. длину ребра ;

2. угол между ребрами 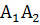и ;

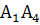3. уравнение грани 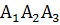и ее площадь;

4. уравнение высоты, опущенной из вершины 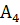на грань .

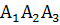Решение:

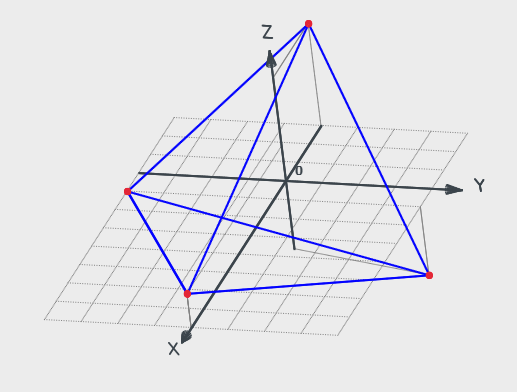
1. Найти длину ребра А₁А₂.

Чтобы найти компоненты вектора нужно из координат его конца вычесть координаты начала. Если заданы точки А(x₁, y₁, z₁), B(x₂, y₂, z₂), то = (x₂ – x₁, y₂ – y₁, z₂ – z₁).

Длина вектора в координатах определяется как расстояние между точками начала и конца вектора. Если заданы две точки в пространстве А(х₁, y₁, z₁), B(x₂, y₂, z₂), то .

В нашем случае:

2. Найти угол между ребрами А₁А₂ и А₁А₄.

Скалярным произведением векторов иназывается число, равное произведению длин этих сторон на косинус угла между ними:=cos.

Если рассматривать векторы в декартовой прямоугольной системе координат, то=x_a x_b + y_a y_b + z_a z_b.

Используя полученные равенства, получаем формулу для вычисления угла между векторами: .

Находим:

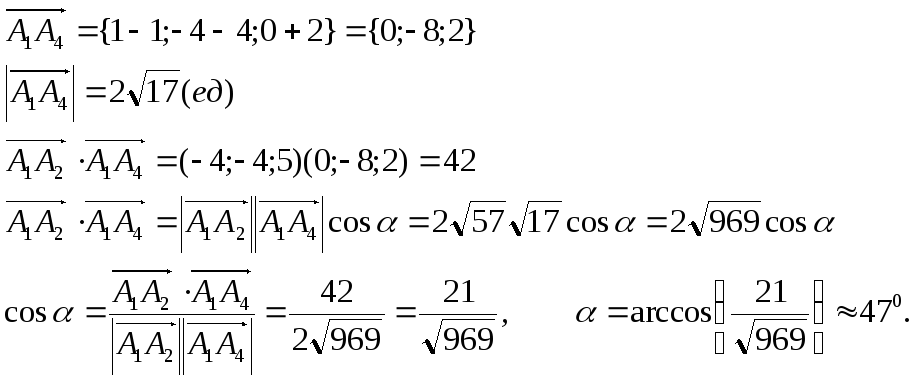
3. Найти уравнение грани и ее площадь.

Воспользуемся формулой уравнения плоскости, проходящей через три точки.

Уравнение плоскости, проходящей через три точки:

,

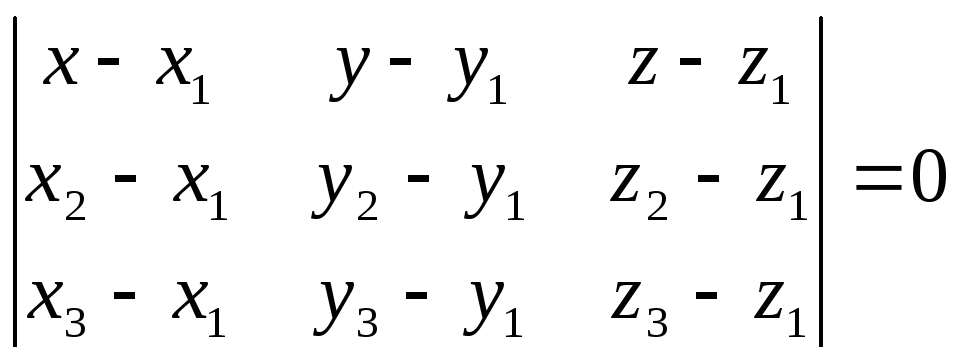
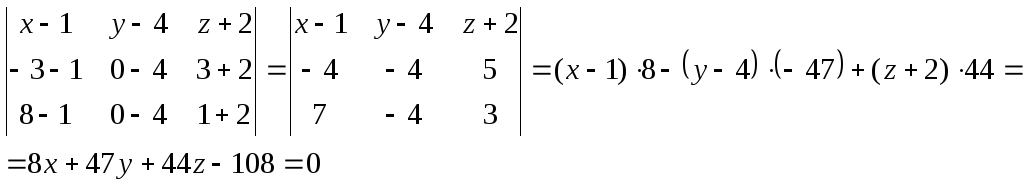
. – уравнение грани .

Вычисляем площадь грани грани :

, .

.

.

.

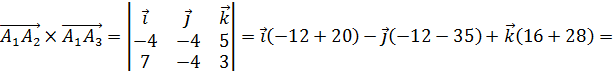
4. Найти уравнение высоты, опущенной из вершины на грань .

Уравнение высоты, будем искать, как уравнение прямой, проходящей через точку   перпендикулярно плоскости  ():

 .

Так как вектор с координатами  является нормальным вектором плоскости , а следовательно, он является направляющим вектором перпендикуляра, опущенного на эту плоскость. Для искомой высоты получим: =.

Ответ: 1) ;

2) ;

3) – уравнение грани , ;

4) =.

Задача 4(39). Составить уравнение множества точек, для каждой из которых выполняется следующее условие: разность расстояний до точек А(0, 10) и О(0,0) равна 8.

Решение:

В задаче говориться о некотором расстоянии до точки A до оси ординат. Обозначим координаты неизвестной точки как С(x,y). В декартовой системе координат расстояние между точками рассчитывается по формуле  (.Тогда расстояние между точками A и C:  . А расстояние до оси ординат будет . Из условия задачи также известно, что . Подставим значения длин AC,CО

;

;

;

;

;

;

;

;

;

;

;

;

;

;

.

Получили уравнение гиперболы с вершиной в точке .

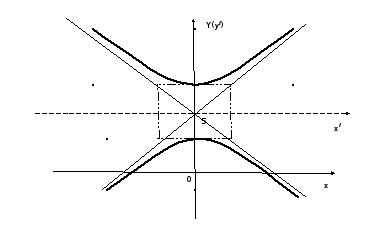
Задача 5(49).

Вычислить пределы функций:

А) ;

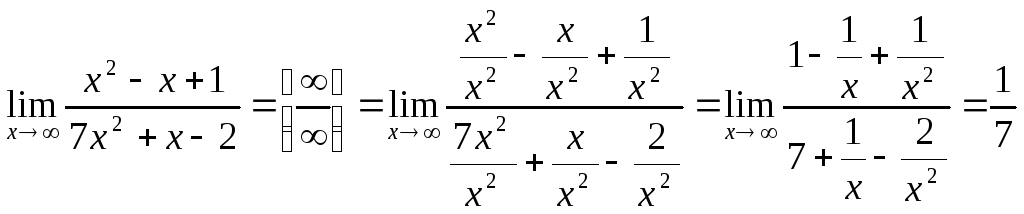Б) ;

В)

.

Задача 6(59).

Задана функция . Найти все точки разрыва функции, если они существуют. Построить график функции.

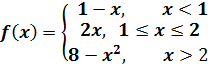
Решение:

Функция определена и непрерывна на интервалах , где она задана непрерывными элементарными функциями. Следовательно, разрыв возможен только в точках и .

Для точки имеем:

, ,

,

т.е. функция в точке имеет разрыв первого рода.

Для точки имеем:

, ,

,

т

y

.е. функция в точке непрерывна.

-1

-1

1

0

1

4

2

2

x