Лабораторная работа №1

Лабораторная работа №1

ИЗУЧЕНИЕ РАВНОУСКОРЕННОГО ДВИЖЕНИЯ

НА МАШИНЕ АТВУДА

Цель работы. Определение ускорения грузов и сравнение результатов, полученных двумя способами.

Приборы и принадлежности. Машина Атвуда, секундомер, перегрузок.

ВВЕДЕНИЕ

Применяемый в данной работе прибор (машина Атвуда – рис. 1) представляет собой вертикальную стойку со шкалой. Сверху на стойке укреплён блок, через который перекинута нить. К обоим концам нитей подвешены грузы с одинаковой массой (см. рисунок). Если на правый груз положить перегрузок, то система грузов и блок начнут двигаться равноускоренно.

Рис. 1. Машина Атвуда.

В данной работе необходимо определить двумя способами ускорение грузов.

1-й способ. Ускорение определяется с помощью формулы равноускоренного движения

(2.1)

где пройденный грузами путь h и время движения t измеряются непосредственно. Из формулы (2.1) следует

(2.2)

2-й способ. Ускорение рассчитывается из рассмотрения энергии системы. Если в замкнутой системе, кроме консервативных, действуют также неконсервативные силы, например силы трения, то полная механическая энергия сохраняется:

Е₂ – Е₁ = А (2.3)

где Е₁ – полая механическая энергия системы в начальном состоянии;

Е₂ – полная механическая энергия системы в конечном состоянии;

А – работа неконсервативных сил.

Силы трения совершают, как правило, отрицательную работу. Поэтому наличие сил трения в замкнутой системе приводит со временем к уменьшению её полной механической энергии. Действие сил трения приводит к превращению механической энергии в другие, немеханические, виды энергии. В этом случае выполняется более общий закон сохранения: в изолированной от любых внешних воздействий системе остаются постоянной сумма всех видов энергии (включая и немеханические).

Грузы, перегрузок, блок и Земля представляют собой замкнутую систему тел, в которой действуют силы трения. В начальный момент система покоится и её кинетическая энергия Т₁ равна нулю. После того как грузы пройдут расстояние h, кинетическая энергия системы станет равной

(2.4)

где М – масса каждого грузов;

m – масса перегрузка;

ω – угловая скорость вращения блока;

V – линейная скорость грузов;

I – момент инерции блока – мера его инерции при вращательном движении.

Первый член справа в равенстве (2.4) представляет собою кинетическую энергию поступательного движения грузов, а второй – кинетическую энергию вращательного движения блока.

Потенциальную энергию системы и её изменение рассчитываем по отношению к конечному положению груза с перегрузком. При движении больших грузов их суммарная потенциальная энергия не изменяется, так как один из них опускается, другой поднимается, а массы их одинаковы. Потенциальная энергия перегрузка в начальный момент равна mgh, в конечный – нулю. Следовательно, изменение потенциальной энергии системы

ΔП = П₂ – П₁ = - mgh.

Изменение полной механической энергии системы

Е₂ – Е₁ = (Т₂ – Т₁) + (П₂ – П₁) =

= (2.5)

В соответствии с равенством (3), изменение полной механической энергии системы равно работе силы трения. Эта работа пропорциональна пройденному пути h и отрицательна, так как сила трения направлена против направления движения системы. Её можно записать так:

А₁ = - F₀h, (2.6)

где F₀ – коэффициент, имеющий размерность силы.

В более общем случае нужно также читывать сопротивление воздуха движению тел. Но в нашем случае, когда тела движутся с малыми скоростями, сопротивление воздуха пренебрежимо мало. С увеличением скорости сопротивление воздуха увеличивается и может оказать влияние на результаты измерения.

При небольших скоростях сила трения а оси блока также может измениться. Поэтому во время проведения опытов высоту h не следует брать больше 20 см.

Из равенства (2.3),(2.5) и (2.6) имеем

= - F₀h.

Так как коэффициент F₀ определить экспериментально трудно, исключим его, рассмотрев движение системы после снятия перегрузка. До остановки грузов система движется замедленно и проходит путь H. На этом участке начальная кинетическая энергия равна , конечная – нулю. потенциальная энергия системы на этом участке не меняется. Таким образом, изменение полной механической энергии системы равно

. (2.7)

На основании равенства (2.3) можно написать:

(2.8)

где А₂ – работа силы трения в оси блока на втором участке. Коэффициент F₀ на обоих участках считается одинаковым.

Решая совместно уравнения (2.7) и (2.8) и учитывая формулу, связывающую угловую скорость с линейной

V = ωR, а также формулу для момента инерции блока

I =

где m₀ – масса блока, R – его радиус, найдём

Используя соотношение для равноускоренного движения V² = 2a₂h, найдём

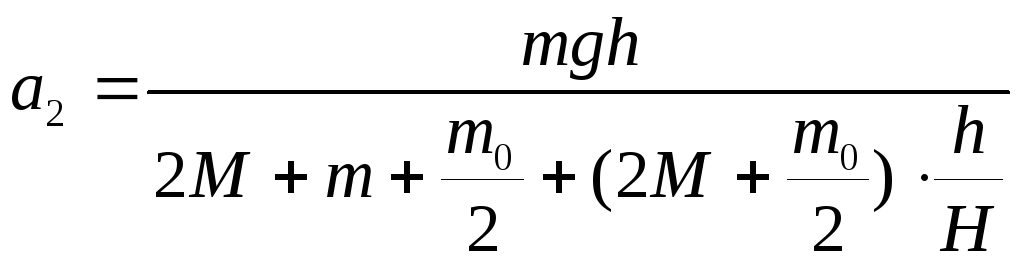(2.9)

Порядок выполнения работы

Выполнение работы производится с ручным режимом запуска секундомера.

1. Ослабить стопорный винт, установить платформу на расстоянии h от начала шкалы и закрепить её.

2. Проверить и отрегулировать вертикальное положение прибора с помощью двух уравнительных винтов, так, чтобы груз проходил через кольцевую платформу, не задевая за её края.

3. Удерживая рукой левый груз, установить правый груз с перегрузком так, чтобы верхний торец груза находился на уровне нулевого отсчёта шкалы машины Атвуда.

4. Отпустить левый груз и включччить секундомер.

5. Измерить время, за которое правый груз пройдёт расстояние h.

6. Измерить расстояние Н.

7. Повторить опыт пять раз с одним и тем же значением высоты h при одном и том же перегрузке m. Изменить высоту h и повторить опыт пять раз с тем же перегрузком. Результаты измерений и вычислений записать в таблицу. Под обозначениями величин обязательно указать единицы их измерения.

Обработка результатов измерений.

1. Рассчитать ускорение грузов а₁ по формуле (2.2). Найти среднее значение.

2. Рассчитать ускорение грузов а₂ по формуле (2.9). Найти среднее значение.

3. Рассчитать погрешность определения а₁ и а₂ по методу Стьюдента Δа₁ и Δа₂.

4. Записать окончательный результат в виде

а₁ = а_1ср ± Δа₁;

а₂ = а_2ср ± Δа₂.

Все данные измерений и расчётов занести в таблицу 2.

Таблица 2

№	h, м	H, м	t, с	a1, м/с2	a2, м/с2
1 2 3 4 5 6 7 8 9 10

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какое движение называется равнопеременным?

2. Почему движение грузов в данной лабораторной работе является равнопеременным?

3. Написать формулы скорости и пути равномерно-ускоренного движения.

4. Какая система тел называется замкнутой?

5. Какие силы называются консервативными?

6. Получить выражение для ускорения грузов из рассмотрения энергии системы.

7. Как выразить работу силы трения в подшипниках блока машины Атвуда, если груз прошёл расстояние h?

8. Как связаны линейная и угловая скорости?

9. Как выражается момент инерции сплошного блока?

ЛИТЕРАТУРА

1. Савельев И.В. Курс общей физики. Т.1. М., Наука, 2003.

2. Детлаф А.А., Яворский Б.М. Курс физики, М., Высшая школа, 1989.

3. Геворкян Р.Г., Шепель В.В., Курс общей физики, - М.,: Высшая школа., 1975.

4. Методические указания к лабораторным работам по физике. Работы 60-63. Раздел «Ошибки измерений физических величин. Вычисление ошибок косвенных измерений». МИИТ, 1976.

11