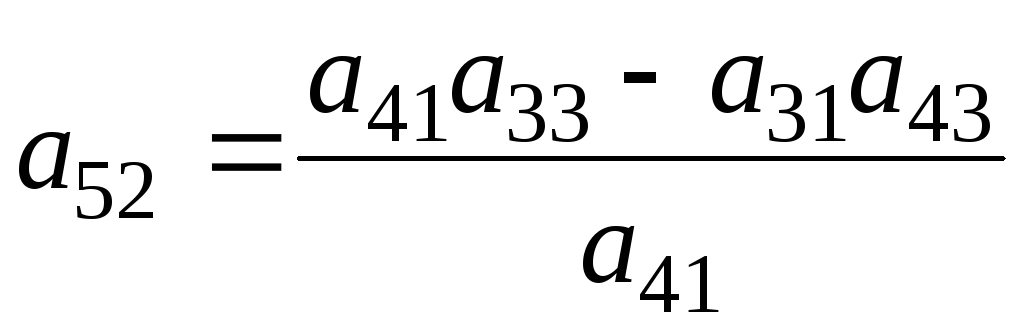3. Устойчивость систем автоматического управления

3.1. Понятие устойчивости линеаризованных систем

У

Рисунок 23. Характеристики

устойчивости системы

стойчивость – это свойство системы возвращаться в исходное состояние после выхода ее из этого состояния и прекращения действия возмущения. Состояние системы может быть устойчивым и нейтральным. Классическим примером этого утверждения является поведение шарика на различных поверхностях (рис. 23): а - устойчивое, безразличное на горизонтальной плоскости, при котором шар может занимать произвольное положение на плоскости; такое равновесие называют нейтрально устойчивым; б - устойчивое в низшей точке впадины криволинейной поверхности, при котором состояние равновесия единственно; в - неустойчивое на вершине «холма»; положение б устойчиво внутри области MN и неустойчиво на ее границе N.

Исходное состояние системы, устойчивость которой необходимо оценить, необязательно является состоянием покоя. Так, например, можно оценить устойчивость движения спутника, как его способность возвращаться на исходную орбиту после прекращения действия сил, отклоняющих спутник от заданной орбиты.

Впервые наиболее существенные математические результаты по устойчивости движения механических систем получил русский ученый А.М. Ляпунов в 1880÷1910 годах, который доказал, что для устойчивости системы необходимым и достаточным условием является отрицательность вещественных частей всех корней характеристического уравнения, т.е. все корни должны располагаться в левой полуплоскости комплексного переменного р.

Рассмотренное условие устойчивости относится к линейным САУ. Но практически все реальные САУ являются нелинейными и только приближенно многие из них можно описывать линейными уравнениями. Ляпунов сформулировал теоремы, позволяющие по устойчивости линеаризованной системы судить об устойчивости исходной нелинейной системы:

1. если линеаризованная система устойчива, то устойчива и исходная нелинейная система;

2. если линеаризованная система неустойчива, то неустойчива и исходная нелинейная система.

3.2. Алгебраические критерии устойчивости

Ранее было сформулировано условие устойчивости линейных систем в виде требований к корням характеристического уравнения. Однако вычисление корней уравнения высокой степени трудно. Поэтому были введены критерии устойчивости, позволяющие судить об устойчивости или неустойчивости системы по коэффициентам характеристического уравнения без вычисления его корней.

Первый алгебраический критерий устойчивости, который применим для систем третьего порядка, сформулировал русский ученый Н.А. Вышнеградский в 1876 г.: для устойчивости линейной системы с характеристическим уравнением a₀p³+a₁p²+a₂p+ a₃ необходимо выполнение двух условий:

1. все коэффициенты характеристического уравнения должны быть положительными;

2. произведение средних коэффициентов должно быть больше произведения крайних, т.е.:

a₁a₂ > a₀a₃.

Для определения устойчивости систем любого порядка применяют критерий Гурвица и критерий Рауса.

По критерию Гурвица система будет устойчива, если определитель Гурвица, все его диагональные миноры и первый коэффициент характеристического уравнения а₀ положительны т.е.: .

Определитель Гурвица строится по коэффициентам характеристического уравнения:

По главной диагонали определителя слева на право выписываются все коэффициенты характеристического уравнения от а₁ до а_n, в порядке возрастания индексов. Столбцы вверх от главной диагонали дополняют коэффициентами характеристического уравнения с последовательно возрастающими индексами. А столбцы вниз - коэффициентами с последовательно убывающими индексами. Максимальный индекс коэффициента n (n - порядок характеристического уравнения), минимальный - нуль. Столбец заполняется до положенного числа n элементов нулями.

Отмечая в определителе Гурвица диагональные миноры, получим определители низшего порядка

.

Номер диагонального минора определяется номером коэффициента по диагонали, для которого составляется минор.

Исследуя с помощью критерия Гурвица устойчивость систем первого, второго, третьего и более высоких порядков, можно сделать вывод: для системы n-го порядка необходимым условием устойчивости является положительность всех коэффициентов.

По критерию Рауса система устойчива, если коэффициент а₀ старшего члена уравнения больше нуля и все элементы первого столбца таблицы Рауса отличны от нуля и положительны.

№ строки	№ столбца
	1	2	3	4
1
2
3
4
5
6	…	…	…	…

Таблица Рауса составляется по следующим правилам: первая строка составляется из четных коэффициентов уравнения (a₀, a₂ и т.д.), а вторая - из нечетных (a₁, a₃ и т.д.), в третью и последующие строки записывается разность произведений коэффициентов, деленная не нечетный коэффициент предыдущей строки, находящийся в первом столбце.

Составление таблицы прерывается, как только первый элемент какой-либо строки оказывается отрицательным или равным нулю.