2.4. Передаточные функции и характеристики разомкнутых систем

С

Рисунок 21. Схемы соединения звеньев

истемы автоматического управления в большинстве случаев являются замкнутыми. Однако при их анализе и проектировании часто предварительно рассматривается разомкнутая цепь звеньев, которая затем замыкается.

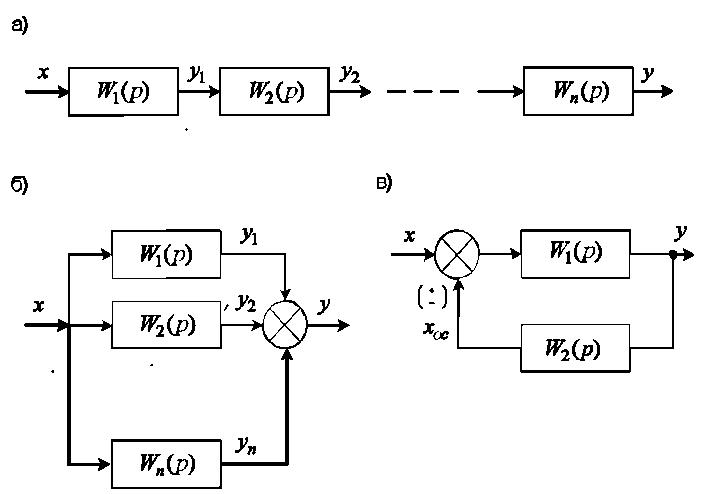
Различают последовательное, параллельное и параллельное с обратной связью соединения звеньев (рис. 21).

1. Последовательным соединением звеньев называют такое соединение, когда выходная величина предыдущего звена, является входной величиной последующего звена (рис.21,а). Если последовательно соединяются звенья m и n, то y_m = x_n.

Передаточная функция всей цепи:

Передаточные функции звеньев:

где: Y (p), Y(p), …, Y_n(p) - изображение по Лапласу соответствующих переменных.

Если перемножить правые и левые части полученных равенств получим:

Поскольку все промежуточные переменные Y ₁(p), Y₂(p), …, Y_n-1(p), при перемножении сократятся, то:

Передаточная функция разомкнутой цепи последовательно соединенных звеньев равна произведению передаточных функций всех звеньев.

Переходя от передаточных функций к частотным характеристикам системы, т.е. полагая что p = jω, получим:

- передаточная функция.

Представив в виде:, находим:

• АЧХ: ;

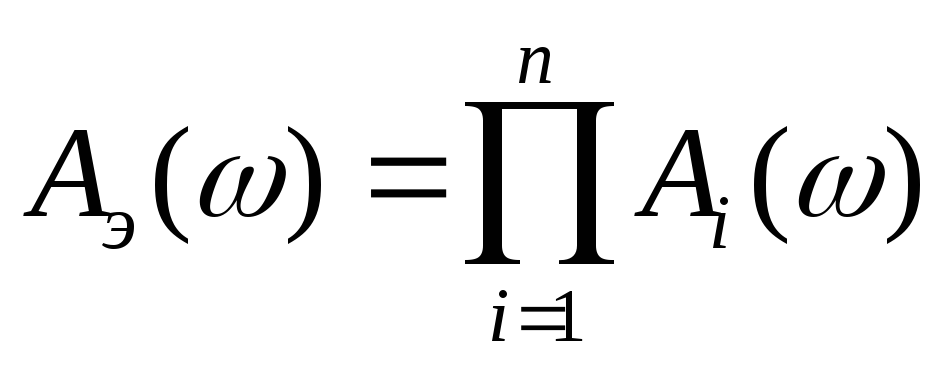• ФЧХ: ;

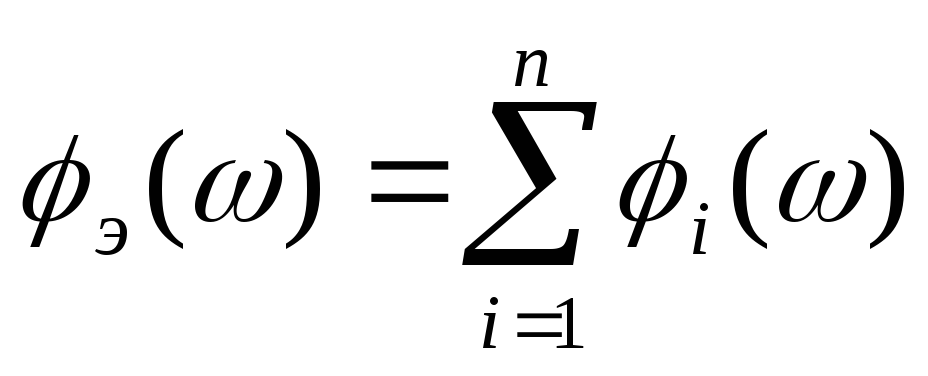• асимптотическая ЛАЧХ:

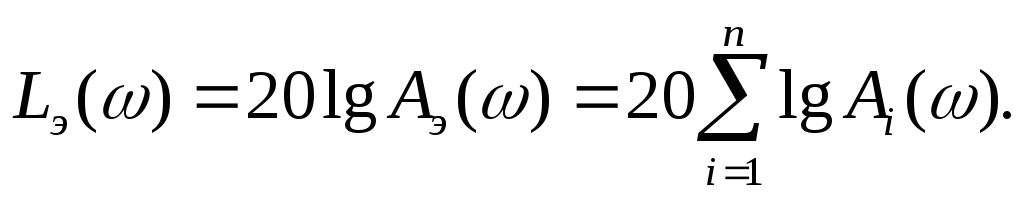
Таким образом, при последовательном соединении звеньев амплитудно-частотные характеристики перемножаются, логарифмически амплитудно-частотные и фазовые частотные характеристики складываются.

Рассмотрим получение частотных характеристик разомкнутой цепи при последовательном соединении звеньев. Пусть передаточная функция разомкнутой цепи имеет вид:

.

Причем 0,5 < ξ < 1 (при таком ξ можно не учитывать «горб» АЧХ колебательного звена).

Логарифмическую асимптотическую АЧХ можно построить непосредственно по передаточной функции. ЛАЧХ является ломанной линией. При этом согласно характеристикам типовых звеньев каждому сомножителю (Tp+1) в знаменателе соответствует точка излома характеристики при  =1/T с последующим наклоном минус 20 дБ/декаду, а каждому сомножителю такого же типа в числителе соответствует точка излома также при  = 1/T, но с последующим наклоном плюс 20 дБ/декаду. Сомножителю типа T²p²+2ξTp+1 в знаменателе соответствует излом характеристики при  =1/T с наклоном минус 40 дБ/декаду.

2. Параллельным соединением звеньев называется такое соединение, когда на входе всех звеньев подается одна и та же величина, а выходные сигналы суммируются (рис. 21,б). Если параллельно соединяются n звеньев, то входной сигнал x = x₁ = …= x_i = …= x_n, а выходной сигнал:

.

Переходя к изображению и учитывая, что Y(p) = W_i(p)∙X_i(p), получим:

,т.е. -передаточная ф-я.

Следовательно:

переходная функция: ,весовая функция: .

Таким образом, при параллельном соединении звеньев передаточные, переходные и весовые функции каждого звена суммируются.

3. При параллельном соединении звеньев с обратной связью обратная связь может быть положительной, если сигнал обратной связи х_ос складывается с входным сигналом х, или отрицательной, если сигнал обратной связи х_ос вычитается из х (рис. 21,в).

При наличии отрицательной обратной связи (ОС) схема описывается следующим уравнением:

.

В свою очередь X_ос(p) определяется в соответствии с выражением:

.

Подставив значение X_ос(p) в выражение для Y(p), получим:

.

Решим это уравнение относительно Y(p):

.

Отсюда:

.

Передаточная характеристика системы при наличии положительной/отрицательной обратной связи:

.

Методика построения ЛАЧХ сводится к следующему (рис. 22):

1. определение сопрягающих частот типовых звеньев в порядке возрастания:

; ;;;;

2

Рисунок 22. Частотные характеристики цепи последовательно соединенных элементов

) вычисление на частоте = 1 ординаты L(1) = 20∙lgk, где k - общий коэффициент передачи разомкнутой системы. Через полученную точку проводят низкочастотную асимптоту ЛАЧХ, представляющую собой при  < 1 прямую с наклоном минус (20∙r) дБ/декаду, где r - число интегрирующих звеньев;

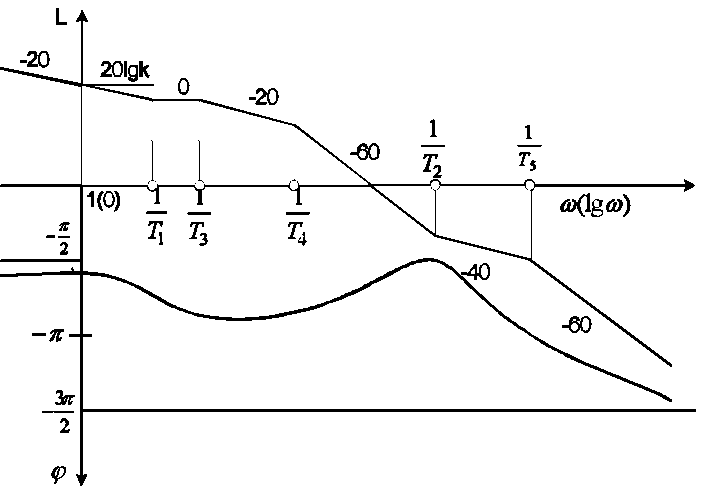
3) изменение наклона ЛАЧХ на сопрягающих частотах по сравнению с тем наклоном, который она имела до рассматриваемой частоты.

Фазовая частотная характеристика (ФЧХ) строится в соответствии с уравнением (рис. 22):