2.3 Задание 5

Задание 5. Определить угол между гранями ABC и ABD.

Линейный угол двугранного угла между плоскостями граней ABC иABDизмеряется в плоскости, перпендикулярной ребруABдвугранного угла. Отсюда следует, что двугранный угол необходимо установить в пространстве так, чтобы реброAB стало перпендикулярным плоскости проекций. В этом случае плоскости гранейABC иABDтакже станут перпендикулярными этой плоскости проекций, а их проекции выродятся в два отрезка, исходящих из одной точки. Угол между этими отрезками и будет являться искомым углом между гранямиABC иABD.

Таким образом, решение задачи сводится к преобразованию ребра ABиз прямой общего положения в проецирующую прямую.

Для решения задачи используем способ замены плоскостей проекций. Преобразование прямой общего положения в проецирующую прямую осуществляется двойной заменой плоскостей проекций. Первой заменой отрезок ABпреобразуем в прямую уровня и второй заменой – в проецирующую прямую.

Последовательность выполнения задания следующая.

На эпюре (рис.8) по заданным координатам (см. таблицу 2) строим два треугольника:ABC -() иABD- (). ТочкиC иD соединять не нужно.

Рис.8. Пример выполнения задания 5

Преобразуем отрезок AB в прямую уровня.

Заменим старую систему взаимно перпендикулярных плоскостей проекций на новую систему также ортогональных плоскостей проекций. Плоскость в пространстве установим параллельно ребруAB. Для этого на эпюре новую ось проекцийнужно расположить параллельно горизонтальной проекции ребра- ||.

Строим новые проекции точек - . При построении новых проекций точек полезно пользоваться правилом – расстояние от новой проекции точки до новой оси проекций равно расстоянию от старой изменяемой проекции точки до старой оси проекций. В нашем случае - это координаты точек(см. рис.8).

В системе плоскостей проекций отрезокABстал параллелен плоскости П₄.

Преобразуем отрезок ABв проецирующую прямую.

Заменим плоскость плоскостью , которую в пространстве установим перпендикулярно ребруAB. В этом случае на эпюре новую ось проекцийнеобходимо расположить перпендикулярно проекции -.

Строим новые проекции точек - . Для построения точек на плоскости проекций на линиях связи от оси проекцийоткладываем значения координат.

На плоскостипроекция ребраABвыродилась в точку, а проекции гранейABC иABD– в прямые линии, угол φ между которыми (рис.8) и является искомым углом.

3. Взаимное пересечение поверхностей (эпюр 3)

Задания 6 и 7 связаны с построением линий пересечения заданных поверхностей.

В задании 6 необходимо построить горизонтальную проекцию шара со сквозным отверстием в виде трехгранной призмы, боковые грани которой перпендикулярны фронтальной плоскости проекций.

В задании 7 необходимо построить линию пересечения заданных поверхностей.

Задания 6 и 7 выполняются в масштабе 1:1 и компонуются на формате А3, согласно рис.9.

При выполнении эпюра видимые контуры заданных тел и видимые участки линии пересечения изображают сплошной основной толстой линией; невидимые - штриховой линией; контуры тел, расположенные внутри других тел, изображают сплошной тонкой линией.

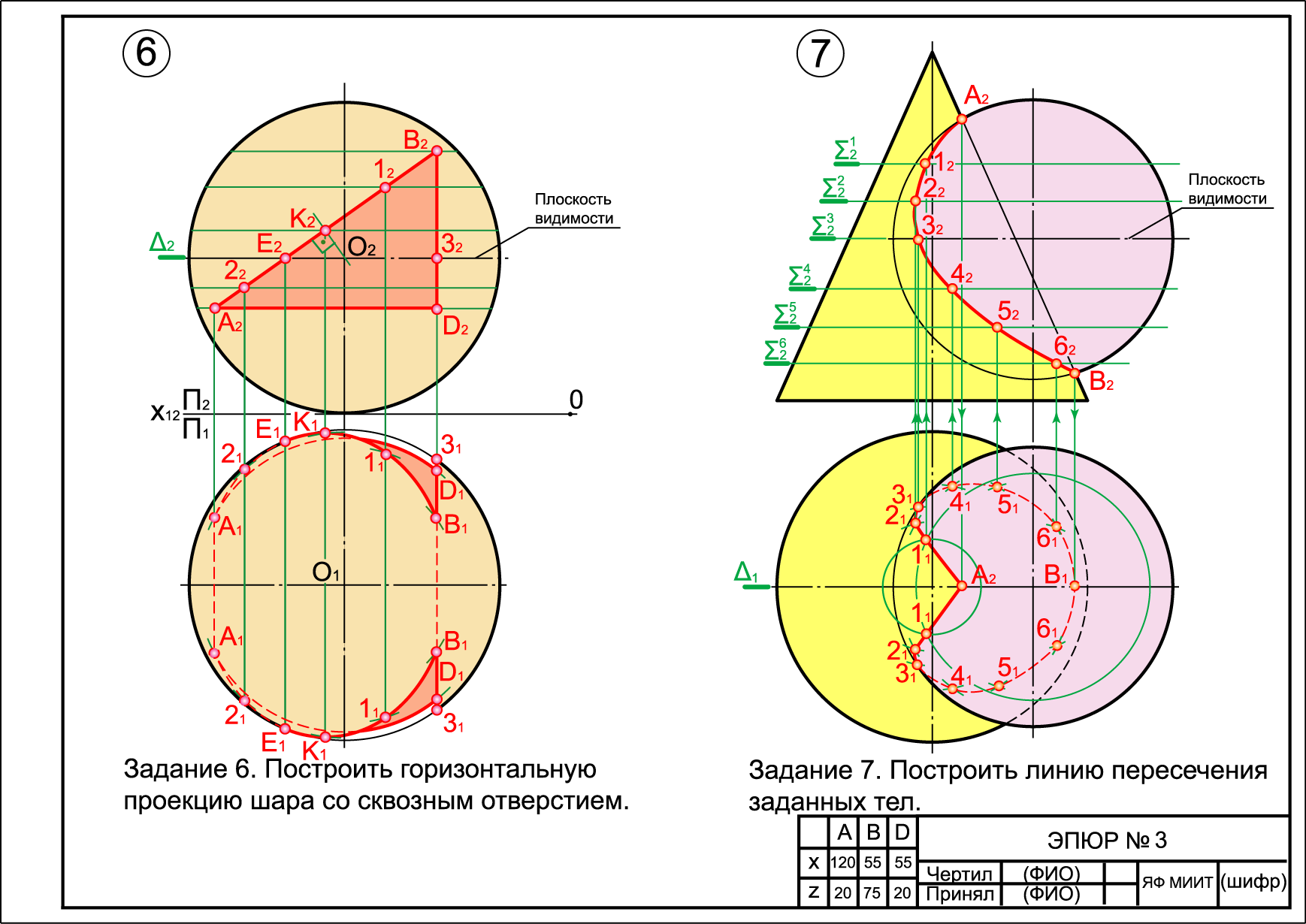
Рис.9. Пример выполнения эпюра №3