2. Уравнение Максвелла в дифференциальной форме.

Уравнения (3-6) записаны в интегральной форме. Гораздо чаще используется дифференциальная форма записи этих уравнений, которая позволяет описать электромагнитное поле в любой точке (точнее в любом элементарном объёме) пространства. Уравнения Максвелла в дифференциальной форме легко получаются из уравнений (3-6) путём применения известных из векторного анализа теорем Остроградского-Гаусса и Стокса, устанавливающих связь между линейными, поверхностными и объёмными интегралами:

Теорема Остроградского-Гауса связывает объёмный интеграл с поверхностным

,

где – скалярная функция – дивергенция (расхождение):

Теорема Стокса связывает поверхностный интеграл с линейным

,

где – векторная функция – ротор (вихрь):

С учётом вышеизложенного уравнения (3-6) принимают вид:

Т.к. объёмы и поверхности, по которым происходит интегрирование произвольны, то можно приравнять подынтегральные функции и получить уравнения Максвелла в дифференциальной форме:

Уравнения Максвелла в дифференциальной форме

(7) (8) (9) (10)

3. Материальные уравнения.

Уравнения Максвелла ещё не составляют полной системы уравнений электромагнитного поля. Этих уравнений недостаточно для нахождения полей по заданным распределениям зарядов и токов. Для этого необходимо дополнить соотношения, в которые входили бы величины, характеризующие индивидуальные свойства среды. Для случая изотропных сред (не содержащих сегнетоэлектриков и ферромагнетиков) они имеют следующий вид:

(11)

С учётом соотношений (11) система уравнений является полной и позволяет описывать все электромагнитные процессы в вакууме и веществе.

4. Свойства уравнений Максвелла.

А. Уравнения Максвелла линейны. Они содержат только первые производные полейипо времени и пространственным координатам, а так же первые степени плотности электрических зарядов ρ и токов γ. Свойство линейности уравнений непосредственно связано с принципом суперпозиции.

Б. Уравнения Максвелла содержат уравнение непрерывности, выражающее закон сохранения электрического заряда:

В.Уравнения Максвелла выполняются во всех инерциальных системах отсчёта. Они являются релятивистски-инвариантными, что подтверждается опытными данными.

Г.О симметрииуравнений Максвелла.

Уравнения не симметричны относительно электрического и магнитного полей. Это обусловлено тем, что в природе существуют электрические заряды, но нет магнитных зарядов. Вместе с тем в нейтральной однородной среде, где ρ = 0 и ,уравнения Максвелла приобретают симметричный вид, т.е.так связано с, какс.

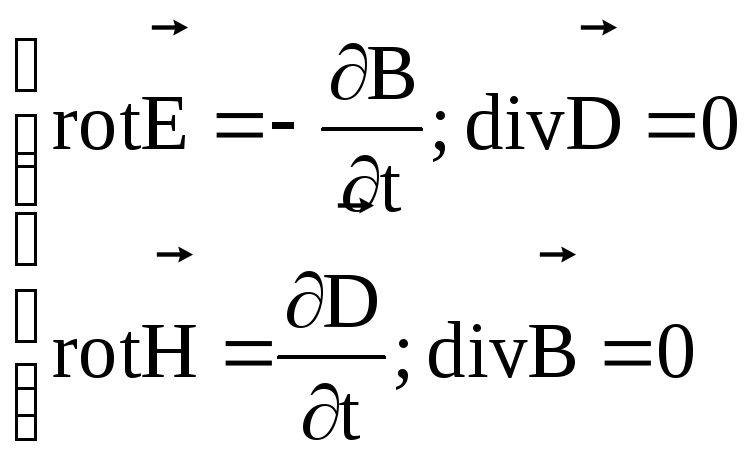
Различие только в знаках перед производными ипоказывает, что линии вихревого электрического поля, индуцированного уменьшением поля, образуют с векторомлевовинтовую систему, в то время как линии магнитного поля, индуцируемого изменением, образуют с векторомправовинтовую систему.

Д. Об электромагнитных волнах.

Из уравнений Максвелла следует важный вывод о существовании принципиально нового физического явления: электромагнитное поле способно существовать самостоятельно без электрических зарядов и токов. При этом изменение его состояния обязательно имеет волновой характер. Всякое изменение во времени магнитного поля возбуждает поле электрическое, изменение электрического поля, в свою очередь, возбуждает магнитное поле. За счёт непрерывного взаимопревращения они и должны сохранятся. Поля такого рода называются электромагнитными волнами. Выяснилось также, что ток смещенияиграет в этом явлении первостепенную роль.