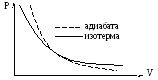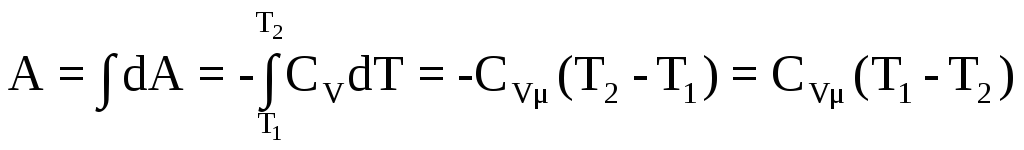Лекция №35. Процессы в газах.

I. Первый закон термодинамики и его применение к изопроцессам в газах.

Если тело не получает извне никакой энергии, то работа А при расширении совершается за счет внутренней энергии U(U= кинетической энергии теплового движения атомов вещества + потенциальной энергии их взаимодействия друг с другом).

Нужно учесть еще и то, что энергия может передаваться от одного тела к другому путем теплопередачи. Эту энергию, называемую количеством тепла Q, будем считать: ΔQ> 0 – тело получает тепло, ΔQ< 0 – тело отдает тепло.

Таким образом, бесконечно малое изменение внутренней энергии складывается из двух частей и может быть записано в дифференциальной форме в виде:

dU= δQδA, (1)

где dU– изменение внутренней энергии тела;

δQ– сообщенное телу количество тепла;

δA– (знак «+») – работа, совершенная внешними силами (сжатие газа); (знак «–») – работа, совершенная телом (расширение газа).

В уравнении (1) QиAне являются полными дифференциалами, т.к. их величины зависят от пути перехода системы из одного состояния в другое, т.е. не являются функциями состояния. Они обычно обозначаются δQи δA(неполный дифференциал).

Уравнение (1) – первое начало термодинамикиили закон сохранения энергии в тепловых процессах. Если произошли конечные изменения системы, то первое начало термодинамики можно записать в виде:

ΔQ= ΔUΔA(2)

Рассмотрим применение первого начала к изопроцессам в газах.

1. Изохорический процесс(V=const)

dU = dQ – dA,

т.к. dA=PdV= 0, то

–

dU=dQ

все подводимое тепло идет на увеличение внутренней энергии

По определению dQ=C_удVmdT, для данного процесса

Т

dU~dT

огда:, т.е. –закон Джоуля

2. Изобарический процесс (P=const)

dU = dQ – dA (3)

По определению для данного процесса:

Подставляя в (3) имеем, с учетом (2):

Используя уравнение состояния: и выражение работыdA=PdV, получим:

C_vμdT=C_pμdT–RdT

C_vμ=C_pμ–R

R=C_pμ–C_vμ

–уравнение Майера (4)

3. Изотермический процесс(T=const)

dU = dQ – dA,

т.к. , то

dQ=dA– подводимое тепло идет на внешнюю работу (расширение).

II. Адиабатический процесс.

Процесс, протекающий без теплообмена с внешней средой, называется адиабатическим(не переходимым).

Адиабатическими можно считать быстропротекающие процессы. Т.к. передачи теплоты нет, то dQ= 0.

dU+dA= 0

Для произвольной массы газа:

Из объединенного газового закона:

По уравнению Майера: R=C_pμ–C_vμи

Обозначим , тогда:интегрируем

lnT+ (γ– 1)V=const→ потенциируем

Уравнение адиабаты идеального газа

TVγ-1=const, (5)

используя уравнение состояния можно получить уравнение адиабаты в координатах PиV.

Уравнение Пуассона

РVγ=const, (6)

Показатель степени в уравнении Пуассона γназываетсяпоказатель адиабаты, т.к. С_Рμ>C_Vμ, тоγ> 1.

Построим график уравнения (6) и сравним его с графиком изотермы.

Вычислим работу при адиабатическом процессе в идеальном газе (для 1 моля) dA+dU= 0, т.к.dU=CvμdT, то Используя уравнение газового состояния,уравнение Майера,уравнение Пуассона, можно получить другие виды формулы работы для адиабатического процесса.

Чтобы вычислить работу для произвольной массы газа mнужно значение работы умножить на число молей:.