
Решение_01
.doc
Контрольная работа №1
Задание 1.1
Построить
математическую модель механической
системы, состоящей из пружины с жесткостью
![]() =104 н/м,
один конец которой закреплен, а на другом
находится тело массой
=104 н/м,
один конец которой закреплен, а на другом
находится тело массой
![]() =1,1 кг.
Тело скользит по горизонтальному
стержню: коэффициент вязкого сопротивления
=1,1 кг.
Тело скользит по горизонтальному
стержню: коэффициент вязкого сопротивления
![]() =0,64 кг/с.
Смещение тела из положения равновесия
равно
=0,64 кг/с.
Смещение тела из положения равновесия
равно
![]() =13 см.
=13 см.
НАЙТИ:
-
амплитуду, частоту и период свободных колебаний механической системы;
-
частоту и период затухающих колебаний системы;
-
уравнение огибающей кривой колебаний;
-
смещение, скорость и ускорение тела в момент времени
 =4 с
для затухающих колебаний.
=4 с
для затухающих колебаний.
Построить графики смещений свободных и затухающих колебаний системы в зависимости от времени.
РЕШЕНИЕ:
Обозначим
через
![]() величину отклонения тела от положения
равновесия в произвольный момент времени
величину отклонения тела от положения
равновесия в произвольный момент времени
![]() .
.
Рассмотрим силы, действующие на колеблющееся тело [1]:
Во-1-х,
это – упругая сила пружины
![]() ,
которая пропорциональна величине
отклонения тела от положения равновесия
,
которая пропорциональна величине
отклонения тела от положения равновесия
![]() и величине жесткости пружины
и величине жесткости пружины
![]() .
Знак «–» показывает, что сила направлена
в сторону, противоположную направлению
отклонения.
.
Знак «–» показывает, что сила направлена
в сторону, противоположную направлению
отклонения.
Во-2-х,
это – сила вязкого трения
![]() ,
которая пропорциональна величине
скорости
,
которая пропорциональна величине
скорости
![]() и коэффициенту вязкого сопротивления
и коэффициенту вязкого сопротивления
![]() .
Знак «–» показывает, что сила направлена
в сторону, противоположную вектору
скорости движения тела.
.
Знак «–» показывает, что сила направлена
в сторону, противоположную вектору
скорости движения тела.
Тогда уравнение движения тела на основании второго закона Ньютона может быть записано в виде
![]() , (1)
, (1)
где
![]() – ускорение.
– ускорение.
Преобразуем
уравнение (1), перенося все слагаемые в
левую часть, разделив на
![]() и введя обозначения:
и введя обозначения:
![]() ,
,
![]() .
.
Получим вместо (1) уравнение
![]() , (2)
, (2)
Уравнение (2) представляет собой обыкновенное дифференциальное уравнение 2-го порядка.
Из условий задачи следует, что уравнение (2) нужно решать для начальных условий вида:
![]() (начальное смещение); (3)
(начальное смещение); (3)
![]() (начальная скорость). (4)
(начальная скорость). (4)
В
случае отсутствия сопротивления среды
(![]() )
уравнение (2) принимает вид
)
уравнение (2) принимает вид
![]() , (5)
, (5)
которое описывает свободные колебания механической системы.
Решая дифференциальное уравнение (5) с условиями (3), (4) в системе maxima [2], получим
(%i1) assume(w0>0);
(%o1) [w0 > 0]
(%i2) ode2('diff(x,t,2)+w0^2*x = 0, x,t);
(%o2) x = %k1 sin(t w0) + %k2 cos(t w0)
(%i3) ic2(%o2,t=0,x=x0,'diff(x,t)=0);
(%o3) x = cos(t w0) x0
Откуда следует, что решение задачи (5), (3), (4) имеет вид
![]() . (6)
. (6)
Выражение
(5) представляет собой синусоидальную
зависимость с круговой частотой
![]() и амплитудой
и амплитудой
![]() .
Подставляя числовые значения исходных
данных, получим:
.
Подставляя числовые значения исходных
данных, получим:
амплитуду
свободных колебаний механической
системы
![]() 0,13 м;
0,13 м;
частоту свободных колебаний механической системы
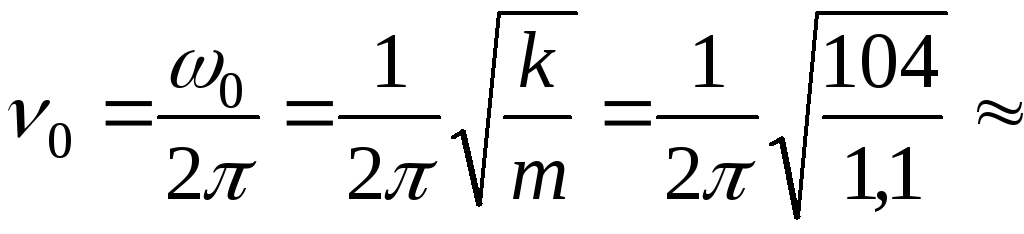 1,5475 Гц;
1,5475 Гц;
период свободных колебаний механической системы
 0,6462 с.
0,6462 с.
График функции (6) (смещений свободных колебаний системы) в зависимости от времени представлен на рисунке 1 (значения по оси ординат указаны в м).
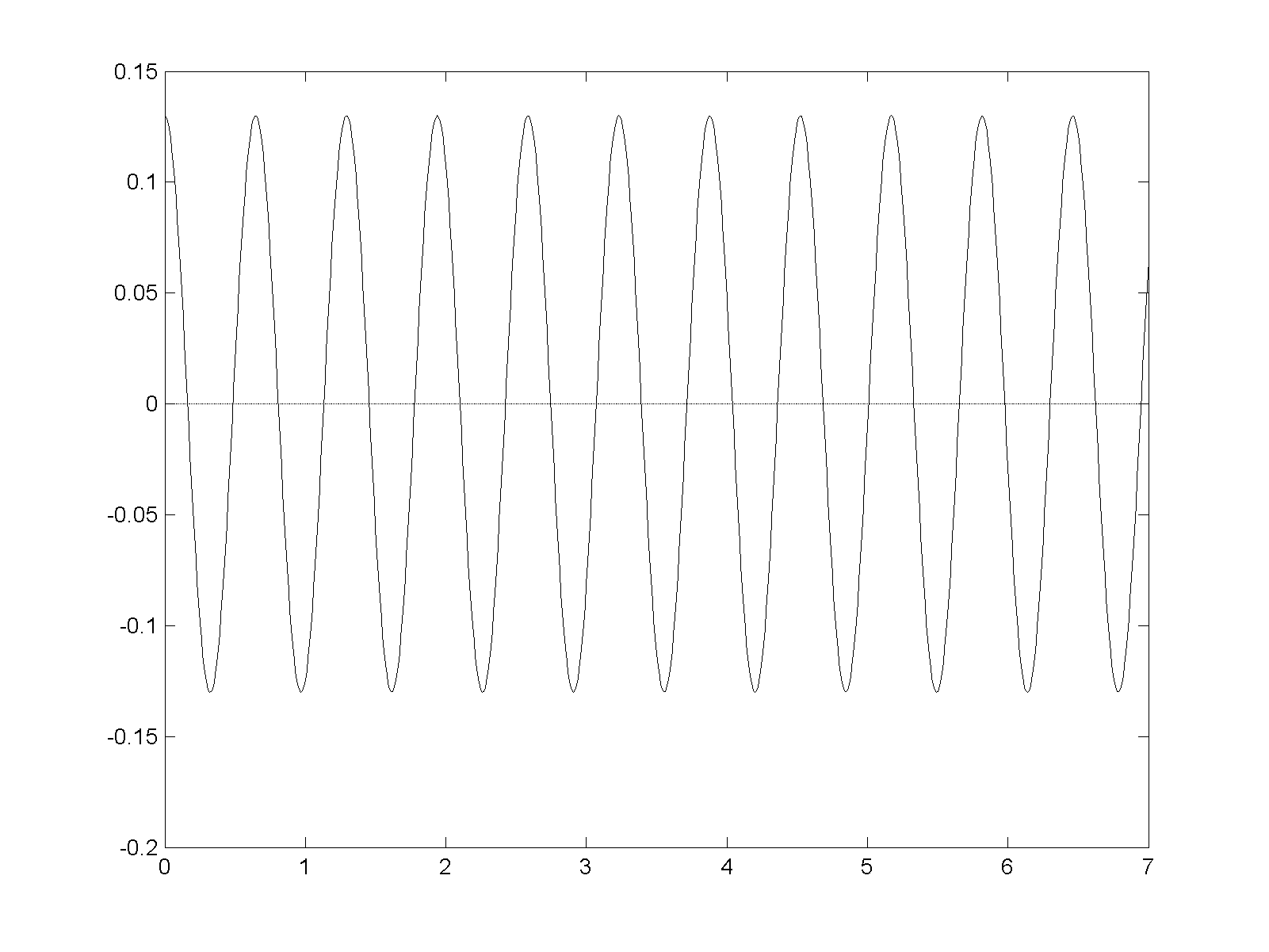
Рисунок 1
Решая дифференциальное уравнение (2) с условиями (3), (4) в системе maxima, получим
(%i1) assume(w0>0);
(%o1) [w0 > 0]
(%i2) assume(b>0);
(%o2) [b > 0]
(%i3) assume(w0-b>0);
(%o3) [w0 > b]
(%i4) ode2('diff(x,t,2)+2*b*'diff(x,t)+w0^2*x = 0, x,t);
2 2
- b t t sqrt(4 w0 - 4 b )
(%o4) x = %e (%k1 sin(--------------------)
2
2 2
t sqrt(4 w0 - 4 b )
+ %k2 cos(--------------------))
2
(%i5) ic2(%o4,t=0,x=x0,'diff(x,t)=0);
2 2
- b t t sqrt(4 w0 - 4 b )
(%o5) x = %e (cos(--------------------) x0
2
2 2
2 2 t sqrt(4 w0 - 4 b )
b sqrt(4 w0 - 4 b ) sin(--------------------) x0
2
- -------------------------------------------------)
2 2
2 b - 2 w0
Откуда следует, что решение задачи (2), (3), (4) имеет вид
![]() , (7)
, (7)
где
![]() .
.
Частота затухающих колебаний системы
 1,5468 Гц;
1,5468 Гц;
период свободных колебаний механической системы
 0,6465 с.
0,6465 с.
Множитель
![]() в выражении (7) представляет собой
огибающую кривой колебаний.
в выражении (7) представляет собой
огибающую кривой колебаний.
Смещение,
скорость и ускорение тела в момент
времени
![]() =4 с
для затухающих колебаний получим по
выражению (7) в maxima, выполняя
дифференцирование выражения (7) (для
скорости и ускорении) и подставляя
числовые значения параметров:
=4 с
для затухающих колебаний получим по
выражению (7) в maxima, выполняя
дифференцирование выражения (7) (для
скорости и ускорении) и подставляя
числовые значения параметров:
(%i1) x(t):=exp(-b*t)*x0*(cos(w*t)+b/w0*sin(w*t));
b
(%o1) x(t) := exp((- b) t) x0 (cos(w t) + -- sin(w t))
w0
(%i2) define(x1(t),diff(x(t),t));
- b t b w cos(t w)
(%o2) x1(t) := %e (------------ - w sin(t w)) x0
w0
- b t b sin(t w)
- b %e (---------- + cos(t w)) x0
w0
(%i3) define(x2(t),diff(x(t),t,2));
2
- b t b w sin(t w) 2
(%o3) x2(t) := %e (- ------------- - w cos(t w)) x0
w0
2 - b t b sin(t w)
+ b %e (---------- + cos(t w)) x0
w0
- b t b w cos(t w)
- 2 b %e (------------ - w sin(t w)) x0
w0
(%i4) k:104; m:1.1; mu:0.64; x0:0.13; T:4;
(%i5) w0:sqrt(k/m); b:mu/(2*m); w:sqrt(w0^2-b^2);
(%i6) x(T);
(%o6) 0.01669190247989552
(%i7) x1(T);
(%o7) - 0.3648095917332507
(%i8) x2(T);
(%o8) - 1.365890653818048
Таким
образом, смещение, скорость и ускорение
тела в момент времени
![]() =4 с
для затухающих колебаний соответственно
равны:
=4 с
для затухающих колебаний соответственно
равны:
![]() 0,0167 м,
0,0167 м,
![]() –0,3648 м/с,
–0,3648 м/с,
![]() –1,3659 м/с2.
–1,3659 м/с2.
График функции (7) (смещений затухающих колебаний системы) в зависимости от времени представлен на рисунке 2 (пунктиром показана огибающая кривой колебаний).

Рисунок 2
ОТВЕТ:
-
 0,13 м;
0,13 м;
 1,547 Гц;
1,547 Гц;
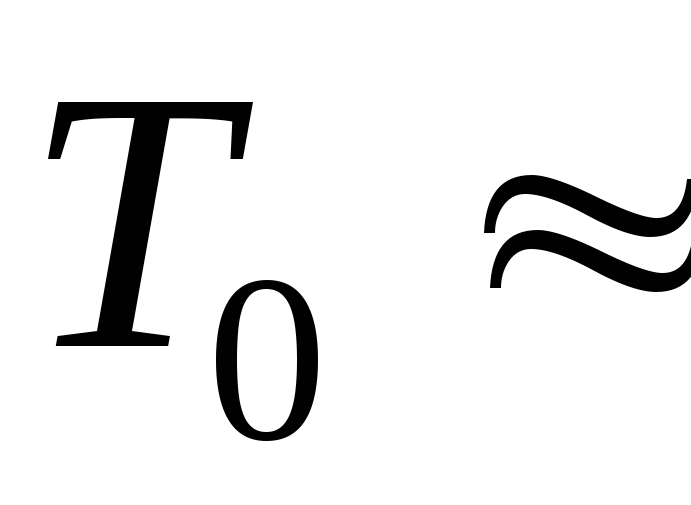 0,646 с;
0,646 с; -
 1,5468 Гц;
1,5468 Гц;
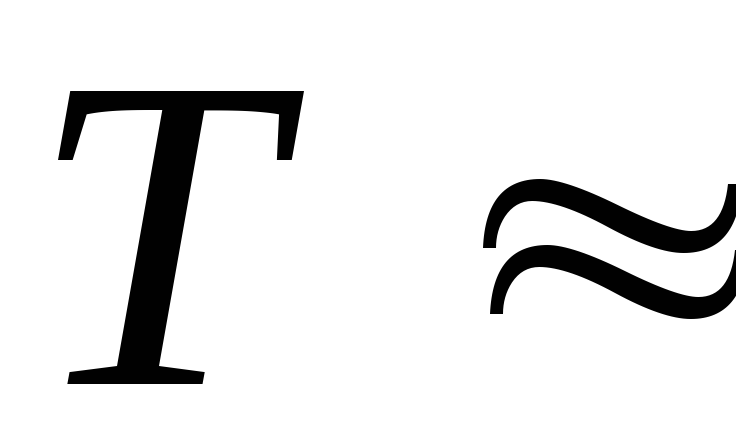 0,6465 с;
0,6465 с; -
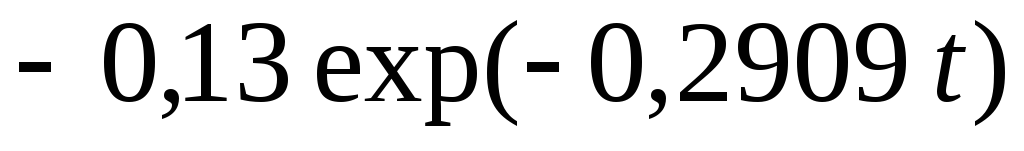 ;
; -
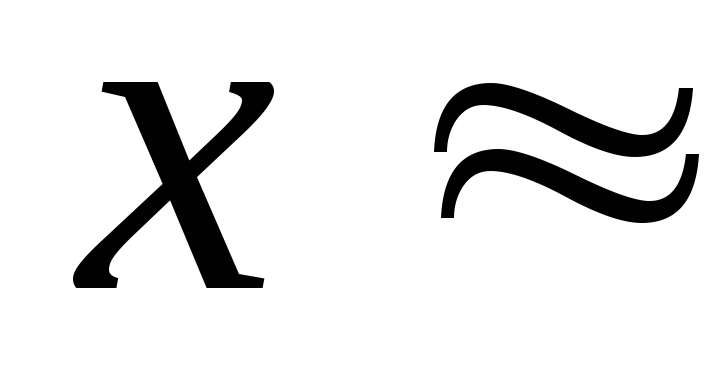 0,0167 м,
0,0167 м,
 –0,3648 м/с,
–0,3648 м/с,
 –1,3659 м/с2.
–1,3659 м/с2.
Задание 1.2
Подводная
лодка водоизмещением
![]() =1170 т
движется горизонтально со скоростью
=1170 т
движется горизонтально со скоростью
![]() 22 км/ч
на глубине
22 км/ч
на глубине
![]() 260 м.
Средняя плотность лодки
260 м.
Средняя плотность лодки
![]() кг/м3.
В момент
кг/м3.
В момент
![]() лодка начинает всплытие. Сопротивлением
воды пренебречь.
лодка начинает всплытие. Сопротивлением
воды пренебречь.
ОПРЕДЕЛИТЬ:
-
время
 ,
когда лодка всплывет на поверхность
моря;
,
когда лодка всплывет на поверхность
моря; -
расстояние
 ,
которое пройдет лодка в горизонтальном
направлении в момент всплытия;
,
которое пройдет лодка в горизонтальном
направлении в момент всплытия; -
вертикальную скорость
 лодки;
лодки; -
траекторию движения подводной лодки в координатах
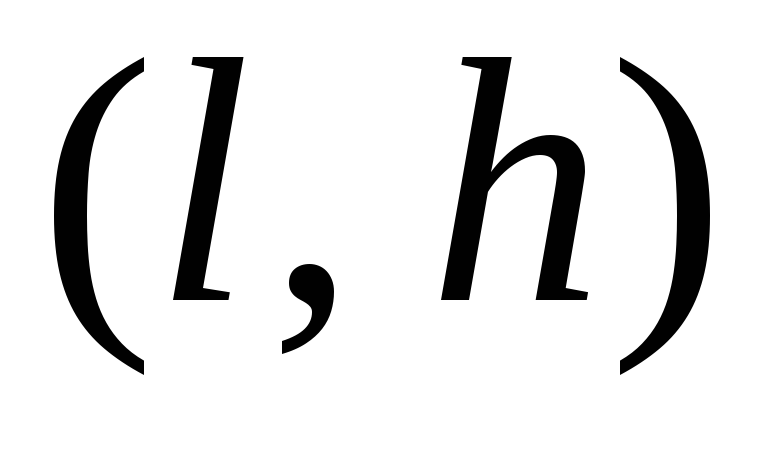 ;
; -
тип соответствующей кривой.
Плотность
воды принять равной
![]() кг/м3.
Сделать чертеж.
кг/м3.
Сделать чертеж.
РЕШЕНИЕ:
Обозначим
через
![]() объем подводной лодки в м3. Тогда
объем подводной лодки в м3. Тогда
![]() ,
где
,
где
![]() – плотность воды. Масса лодки во время
всплытия может быть определена
произведением
– плотность воды. Масса лодки во время
всплытия может быть определена
произведением
![]() .
На лодку вертикально вверх действует
выталкивающая сила Архимеда [3]
.
На лодку вертикально вверх действует
выталкивающая сила Архимеда [3]
![]() ,
где
,
где
![]() – ускорение свободного падения. Также
в вертикальном направлении – но уже
вниз – на лодку действует сила тяжести
(вес лодки)
– ускорение свободного падения. Также
в вертикальном направлении – но уже
вниз – на лодку действует сила тяжести
(вес лодки)
![]() .
Положительная разность сил
.
Положительная разность сил
![]() и
и
![]() обеспечивает подъем лодки в вертикальном
направлении
обеспечивает подъем лодки в вертикальном
направлении
![]() .
Уравнение движения лодки по координате
.
Уравнение движения лодки по координате
![]() может быть записано в виде
может быть записано в виде
![]() , (1)
, (1)
где
![]() – ускорение движения лодки в вертикальном
направлении (
– ускорение движения лодки в вертикальном
направлении (![]() отсчитывается от поверхности моря
вглубь моря). То, что
отсчитывается от поверхности моря
вглубь моря). То, что
![]() показывает, что лодка должна всплывать.
показывает, что лодка должна всплывать.
Перенесем
отсчет времени на момент
![]() и запишем задачу Коши для уравнения (1)
в виде
и запишем задачу Коши для уравнения (1)
в виде
![]() ,
,
или ![]() , (1)
, (1)
![]() ,
,
![]() (вертикальная скорость в начальный
момент). (2)
(вертикальная скорость в начальный
момент). (2)
Решим задачу (1), (2) в математическом пакете maxima [2]:
(%i1) ode2('diff(h,t,2) =(r1-r0)/r1*g, h,t);
2
(r1 - r0) t
(%o1) h = ------------ g + %k2 t + %k1
2 r1
(%i2) ic2(%o1,t=0,h=H,'diff(h,t)=0);
2
(r1 - r0) t
(%o2) h = H + ------------ g
2 r1
Откуда,
следует, что выражение глубины погружения
![]() в зависимости от скорректированного
времени
в зависимости от скорректированного
времени
![]() имеет вид
имеет вид
![]() . (3)
. (3)
Момент
времени
![]() ,
когда лодка всплывет на поверхность
моря, определим по значению
,
когда лодка всплывет на поверхность
моря, определим по значению
![]() из выражения (3) при котором
из выражения (3) при котором
![]() .
Решая уравнение
.
Решая уравнение
![]() ,
,
получим
![]() .
Подставляя числовые значения параметров,
получим
.
Подставляя числовые значения параметров,
получим
 17,3 с. (4)
17,3 с. (4)
Таким
образом,
![]() 17,3 с.
17,3 с.
На
рисунке 3 показан график зависимости
![]() при изменении времени от
при изменении времени от
![]() до
до
![]() .
.
По
горизонтали
![]() лодка перемещается равномерно со
скоростью
лодка перемещается равномерно со
скоростью
![]() .
Следовательно, зависимость
.
Следовательно, зависимость
![]() от времени можно представить линейной
связью
от времени можно представить линейной
связью
![]() . (5)
. (5)
Подставляя
в (5) время всплытия
![]() ,
получим расстояние
,
получим расстояние
![]() ,
которое пройдет лодка в горизонтальном
направлении от начала до окончания
этапа всплытия
,
которое пройдет лодка в горизонтальном
направлении от начала до окончания
этапа всплытия
![]() 22000/3600
∙ 17,3
22000/3600
∙ 17,3![]() 105,7 м.
105,7 м.

Рисунок 3
Для
нахождения вертикальной скорости лодки
достаточно продифференцировать по
![]() выражение (3)
выражение (3)
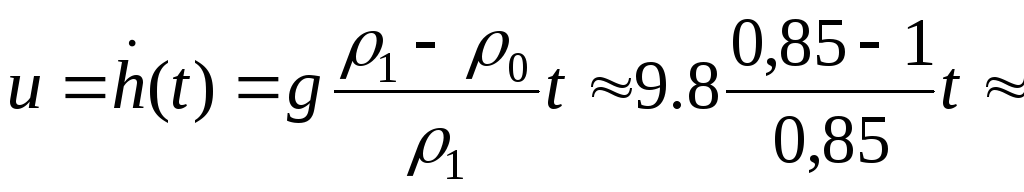 –1,7
–1,7![]() м/с (6)
м/с (6)
(отрицательное
значение
![]() показывает, что глубина с течением
времени уменьшается).
показывает, что глубина с течением
времени уменьшается).
Выражая
из (5) время
![]() через координату
через координату
![]() и подставляя это выражение в (3), получим
связь между глубиной
и подставляя это выражение в (3), получим
связь между глубиной
![]() и горизонтальным расстоянием
и горизонтальным расстоянием
![]() от точки начала всплытия
от точки начала всплытия
![]() . (7)
. (7)
Подставляя числовые значения параметров, получим
![]() . (8)
. (8)
Форма
зависимостей (7), (8) показывает, что график
соответствующей кривой имеет форму
параболы. На рисунке 4 представлен этот
график в интервале изменения
![]() от 0 до
от 0 до
![]() .
.

Рисунок 4
ОТВЕТ:
-
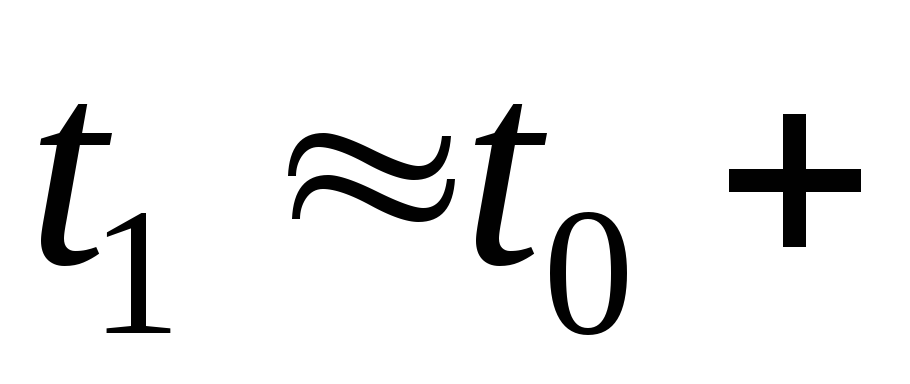 17,3 с;
17,3 с; -
 105,7 м;
105,7 м; -
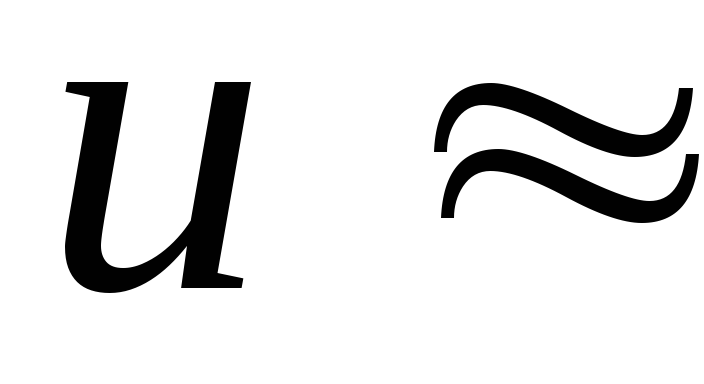 –1,7
–1,7 м/с;
м/с; -
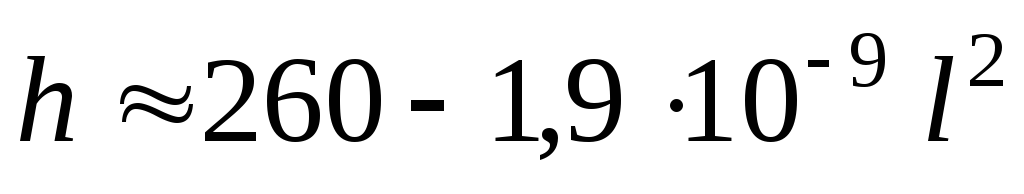 ;
; -
тип кривой – парабола.
Список литературы
-
Кингсеп, А.С. Основы физики: Курс общей физики : Учебник для вузов. Т.1. Механика,электричество и магнетизм,колебания и волны,волновая оптика / А.С. Кингсеп, Г.Р. Локшин, О.А. Ольхов.– М. : Физматлит, 2001.– 560с.
-
URL: http://maxima.sourceforge.net/documentation.html
-
Ландау, Л.Д. Теоретическая физика : Учеб.пособие:В 10 т. Т.VI. Гидродинамика / Л.Д. Ландау, Е.М. Лифшиц – М. : Физматлит, 2001.– 736с
