Решение_02

7

Контрольная работа №2

Задание 2.1

Пусть заданы координаты точек (-5;5) и (15;15). Точка лежит на прямой . Используя вариационные принципы построения математических моделей,

НАЙТИ:

1. условие, при котором ломаная 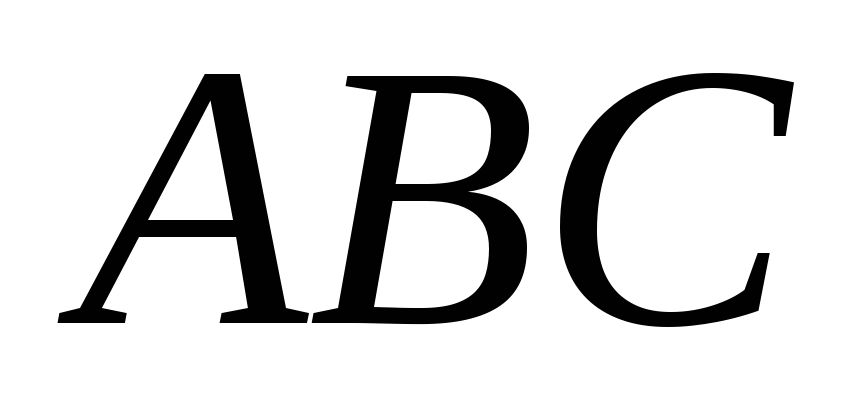имеет наименьшую длину;

2. числовое значение этого условия;

3. наименьшую длину ломаной .

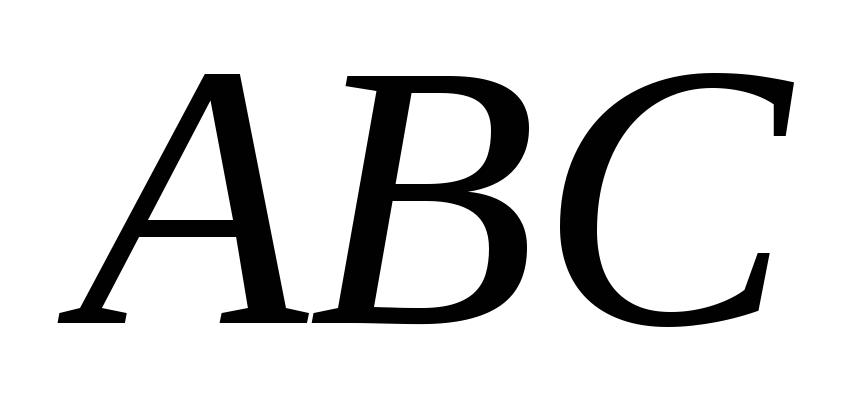РЕШЕНИЕ:

По условию координаты точки имеют вид . Длина ломаной определяется суммой длин отрезков и

. (1)

Используя формулу определения расстояния между двумя точками, получим

,

или (с учетом заданных числовых значений)

. (2)

По условию задачи надо найти такое , которое минимизирует , т.е. обеспечивает

. (3)

Заметим, других ограничений на переменную нет, следовательно, задача (3) представляет собой одномерную задачу безусловной оптимизации [1]. В данном случае она формулируется как задача поиска минимума непрерывной дифференцируемой функции (2).

При этом можно принять в расчет следующее очевидное соображение, в котором учитывается взаимное расположение заданных точек и (точка расположена правее точки по оси ). Поскольку при точка будет находиться на минимальном расстоянии от точки , то дальнейшее смещение точки влево будет увеличивать и и . Следовательно искомое значение не может быть меньше . Аналогично можно заметить, что искомое значение не может быть больше – координаты точки , расположенной правее.

Следовательно, в дополнение к целевой функции (3) можно добавить условие

. (4)

Тогда задача (3), (4) будет задачей условной оптимизации.

Для поиска минимума функции найдем корни ее производной. Вычисление производной и поиск корней выполним с помощью математического пакета maxima [2]:

(%i1) L(x):=sqrt((x+5)^2+5^2)+sqrt((15-x)^2+15^2);

2 2 2 2

(%o1) L(x) := sqrt((x + 5) + 5 ) + sqrt((15 - x) + 15 )

(%i2) define(L1(x),diff(L(x),x));

x + 5 15 - x

(%o2) L1(x) := ------------------- - ---------------------

2 2

sqrt((x + 5) + 25) sqrt((15 - x) + 225)

(%i3) x0:find_root(L1(x)=0,x,-5,15);

(%o3) 0.0

(%i4) eps:0.0001;

(%o4) 1.0e-4

(%i5) L1(x0-eps);

(%o5) - 9.428184697735098e-6

(%i6) L1(x0+eps);

(%o6) 9.427996135902283e-6

(%i7) L(x0);

(%o7) 28.2842712474619

Таким образом, на отрезке (4) найден один корень уравнения

. (5)

Этот корень равен 0 (см. (%o3)). Командами (%i5), (%i6) точка проверена на экстремальность: она не является точкой перегиба и в ней достигается минимум функции , поскольку знак производной в меняется с «–» на «+».

Минимальное значение функции в точке равно

28,284.

ОТВЕТ:

1. , ;

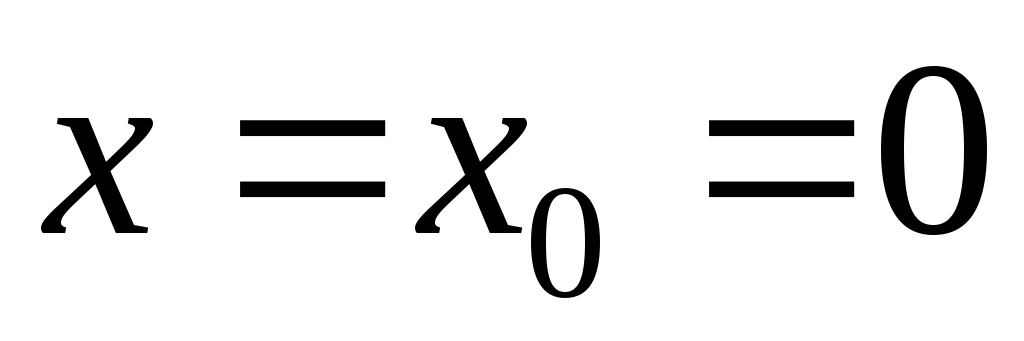2. , 28,284;

3. наименьшая длина ломаной 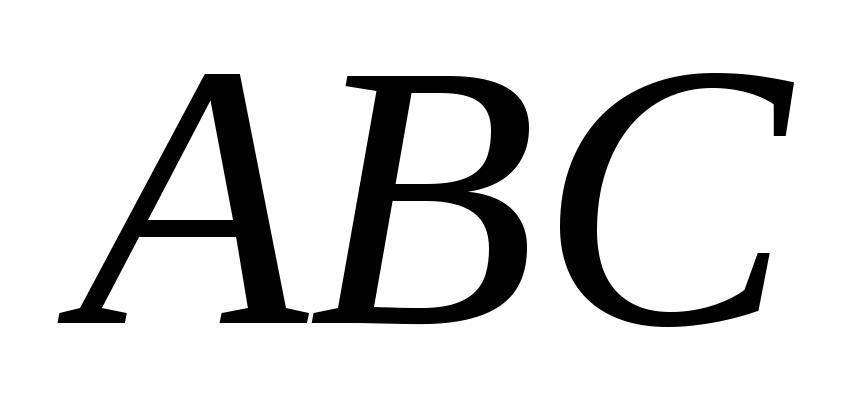равна 28,284.

Задание 2.2

Провести идентификацию эмпирической математической модели.

А) Предполагается, что процесс описывается одномерным уравнением 2-го порядка

, . (1)

Б) Предполагается, что процесс описывается одномерным уравнением 3-го порядка

, . (2)

Считаем, что величина измерена точно, а – с ошибкой , имеющей нормальное распределение с нулевым математическим ожиданием () и единичной дисперсией (). Проверить адекватность модели методом Фишера и сравнить модели А) и Б) с моделью линейной регрессии.

Таблица

Исходные данные

№ точки	1	2	3	4	5	6	7	8	9	10	11
	0	1	2	3	4	5	6	7	8	9	10
	21,1	20,7	32,7	40,8	54,6	53,4	66,5	77,7	81,6	88,8	98,3

РЕШЕНИЕ:

Для расчета коэффициентов , , , моделей (1), (2) использовалась процедура linear_regression математического пакета maxima. Входным параметром процедуры является матрица, в первых столбцах которой формируются значения аргументов (независимых факторов) модели (, , ), а в последнем – значения зависимого фактора (). В выходных параметрах процедуры представлены рассчитанные значения коэффициентов , , ,… и некоторые статистические оценки полученной модели.

Для получения коэффициентов , , параболической модели (1) последовательность команд для формирования параметров и вызова процедура linear_regression представлена ниже:

(%i1) load("stats")$

(%i2) N:11$ M:zeromatrix(N,2)$

(%i4) Y:[21.1, 20.7, 32.7, 40.8, 54.6, 53.4, 66.5, 77.7, 81.6, 88.8, 98.3]$

(%i5) for i:0 thru N-1 step 1 do (M[i+1,1]:i,M[i+1,2]:i^2)$

(%i6) M:addcol(M,Y)$

(%i7) linear_regression(M);

(%o7) inference_result([LINEAR REGRESSION MODEL],

[b_estimation = [17.32447552447547, 8.11216783216787,

- 0.001398601398605592]], [b_statistics =

[6.516319842387226, 6.558197859331842, - 0.01173953585387314]],

[b_p_values = [1.848992656008352e-4, 1.769481669655626e-4,

0.9909209005665658]], [b_distribution = [student_t, 8]],

[v_estimation = 12.17792657342658], [v_conf_int =

[5.556084076110339, 44.69515912009124]], [v_distribution = [chi2, 8]],

[adc = 0.9833436587189254])

В блоке выходных параметров b_estimation представлены рассчитанные значения коэффициентов , , . Таким образом, модель (1) принимает вид

. (3)

Для проверки адекватности модели по критерию Фишера рассчитываются характеристики разброса функции , учтенные в модели – и неучтенные – [3].

Величина рассчитывается по модельным значениям и среднему значению наблюдаемых значений (из таблицы 1)

(4)

где – общее число наблюдений (в рассматриваемом случае ); – число параметров модели (кроме ). В случае модели (3) 2.

Численное значение 3606,9.

Величина рассчитывается по модельным значениям и всем наблюдаемым значениям (из таблицы)

(5)

Численное значение 12,1779 (заметим, оно рассчитывается в качестве выходного параметра v_estimation в linear_regression, см. выше).

Далее рассчитывается экспериментальное значение критерия Фишера

, (6)

Таким образом, 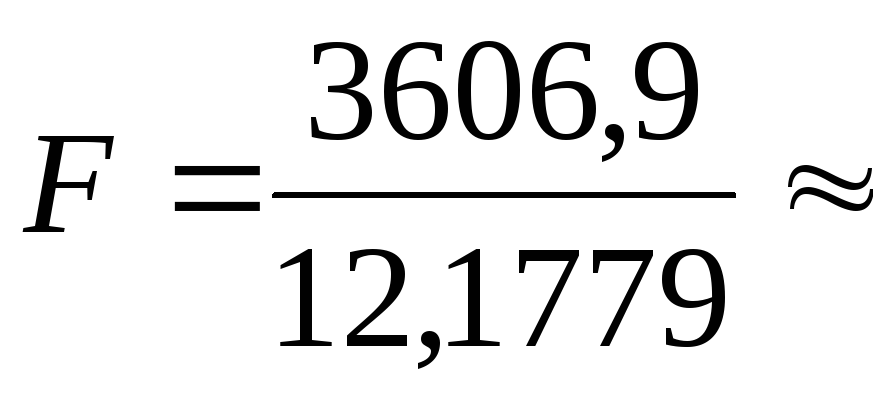296,2.

Сравнивая расчетное значение параметра с табличным значением 4,459 [3], убеждаемся что . Следовательно, модель (1)/(3) является адекватной по критерию Фишера.

Проведем расчет коэффициентов , , , модели третьей степени (2):

(%i1) load("stats")$

(%i2) N:11$ M:zeromatrix(N,3)$

(%i4) Y:[21.1, 20.7, 32.7, 40.8, 54.6, 53.4, 66.5, 77.7, 81.6, 88.8, 98.3]$

(%i5) for i:0 thru N-1 step 1 do (M[i+1,1]:i,M[i+1,2]:i^2,M[i+1,3]:i^3)$

(%i6) M:addcol(M,Y)$

(%i7) linear_regression(M);

(%o7) inference_result([LINEAR REGRESSION MODEL],

[b_estimation = [18.60909090909036, 6.071056721056721, 0.5338578088578743,

- 0.03568376068376011]], [b_statistics =

[5.852649504238012, 2.096778199845873, 0.7698443841032158,

- 0.7841137546322967]], [b_p_values = [6.2890748428579e-4,

0.07422345322107571, 0.4665721055243981, 0.4586802673966752]],

[b_distribution = [student_t, 7]], [v_estimation = 12.79389776889779],

[v_conf_int = [5.59286846707532, 52.9965783187945]],

[v_distribution = [chi2, 7]], [adc = 0.9825011650161413])

Таким образом, модель (2) принимает вид

. (7)

Для проверки адекватности модели по критерию Фишера также рассчитываются параметры и , а затем и по формулам (4)-(6) с учетом того, что 3.

Значение 188,155, табличное значение 4,347. Поскольку то и модель (2)/(3) является адекватной по критерию Фишера.

Для построения линейной модели также используем процедуру linear_regression:

(%i1) load("stats")$

(%i2) N:11$ M:zeromatrix(N,1)$

(%i4) Y:[21.1, 20.7, 32.7, 40.8, 54.6, 53.4, 66.5, 77.7, 81.6, 88.8, 98.3]$

(%i5) for i:0 thru N-1 step 1 do (M[i+1,1]:i)$

(%i6) M:addcol(M,Y)$

(%i7) linear_regression(M);

| LINEAR REGRESSION MODEL

|

| b_estimation = [17.34545454545452, 8.098181818181821]

|

| b_statistics = [9.346173749228656, 25.8148562276811]

|

| b_p_values = [6.263543545381722e-6, 9.466893935439202e-10]

|

(%o7) | b_distribution = [student_t, 9]

|

| v_estimation = 10.8250101010101

|

| v_conf_int = [5.12149924450257, 36.07816239464696]

|

| v_distribution = [chi2, 9]

|

| adc = 0.9851941082477088

Из чего следует, что линейная модель имеет вид

.

Эта модель также является адекватной по критерию Фишера.

На рисунке 1 представлены графики зависимостей (утолщенная сплошная линия) и (пунктирная линия). Также маркерами вида «х» на графике представлены исходные данные. Видно, что регрессионные модели достаточно хорошо отражают зависимость от . Графики показывают, что линии и практически не различимы. Следовательно, можно ограничиться линейной моделью (8).

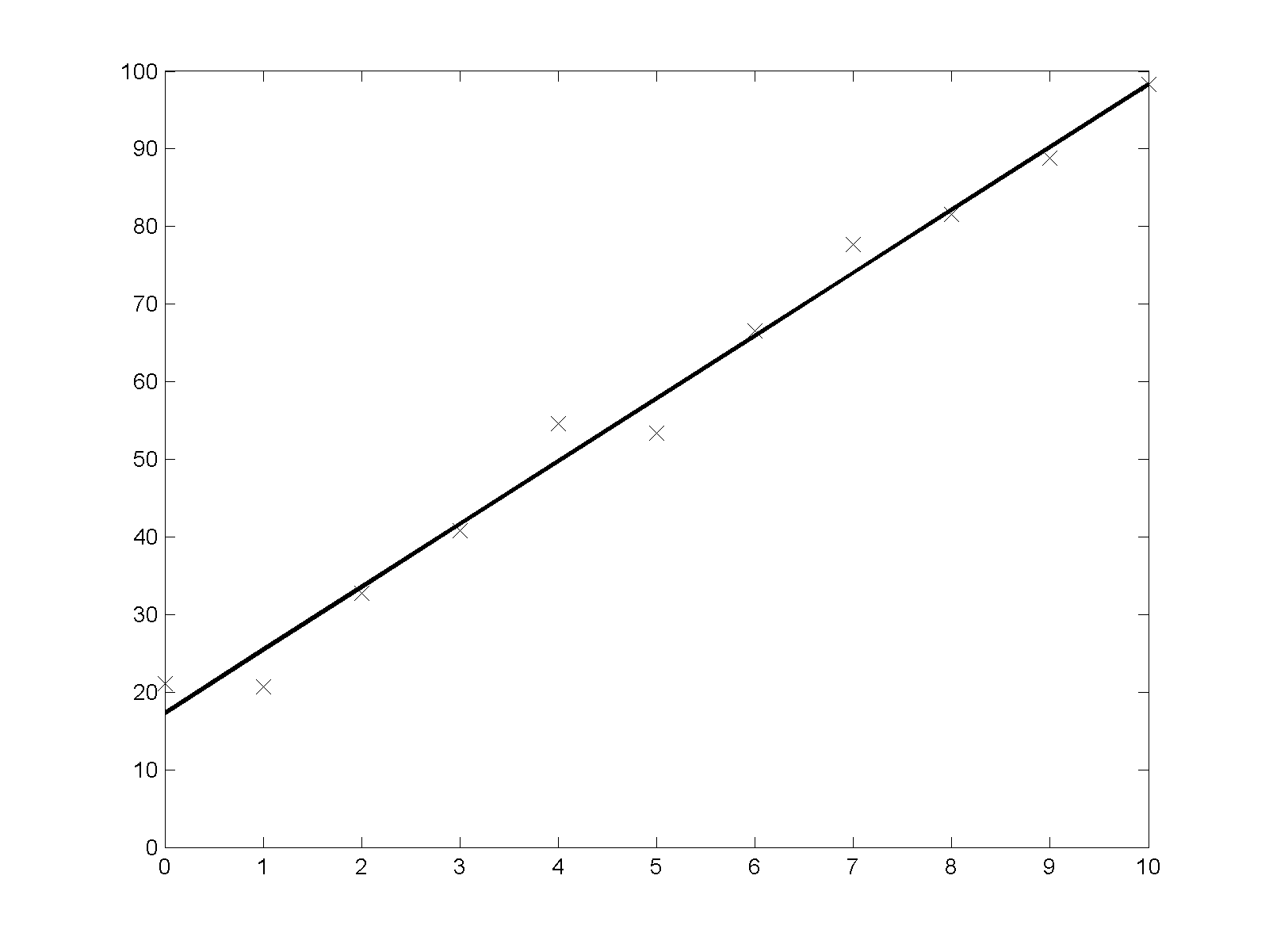
Рисунок 1

На рисунке 2 аналогично представлены зависимости для двух моделей и . В этом случае наблюдается некоторое отличие графиков. На кривой явно выражены нелинейные участки. Но для того, чтобы проверить, действительно ли в связи и есть нелинейные составляющие следует провести дополнительную серию экспериментов.

Рисунок 2

Список литературы

1. Краснов, М.Л. Вариационное исчисление. Задачи и примеры с подробными решениями: учебное пособие для вузов / М.Л. Краснов, Г.И. Макаренко, А.И. Киселев.– М. : УРСС, 2002.– 176с.

2. URL: http://maxima.sourceforge.net/documentation.html

3. Елисеева, И.И. Эконометрика : учебник для вузов / И.И. Елисеева [и др].; под. ред. И.И. Елисеевой.– М. : Финансы и статистика, 2007.– 576с.