Крипто / Билет №10

Билет №10

Эллиптическая криптография — раздел криптографии, который изучает асимметричные криптосистемы, основанные на эллиптических кривых над конечными полями. Основное преимущество эллиптической криптографии заключается в том, что на сегодняшний день неизвестно существование субэкспоненциальных алгоритмов решения задачи дискретного логарифмирования. Использование эллиптических кривых для создания криптосистем было независимо предложено Нилом Коблицем (англ.) и Виктором Миллером (англ.) в 1985 году.

Эллиптические кривые над конечными полями[править | править исходный текст]

Основная статья: Эллиптическая кривая

Эллиптической кривой называется множество точек , удовлетворяющих уравнению:

Это уравнение может рассматриваться над произвольными полями и, в частности, над конечными полями, представляющими для криптографии особый интерес.

В криптографии эллиптические кривые рассматриваются над двумя типами конечных полей: простыми полями нечётной характеристики (, где  — простое число) и полями характеристики 2 ().

Эллиптические кривые над полями нечётной характеристики[править | править исходный текст]

Над полем  характеристики  уравнение эллиптической кривой E можно привести к виду:

где  — константы, удовлетворяющие .

Группой точек эллиптической кривой E над полем  называется множество пар , лежащих на E, объединённое с нулевым элементом :

Следует отметить, что в  у каждого ненулевого элемента есть либо два квадратных корня, либо нет ни одного, поэтому точки эллиптической кривой разбиваются на пары вида  и .

Пример[править | править исходный текст]

Рассмотрим эллиптическую кривую  над полем . На этой кривой в частности лежит точка , так как .

Теорема Хассе[править | править исходный текст]

Теорема Хассе об эллиптических кривых утверждает, что количество точек на эллиптической кривой близко к размеру конечного поля:

что влечёт:

Эллиптические кривые над полями характеристики 2[править | править исходный текст]

Над полем характеристики 2 рассматривают два вида эллиптических кривых:

• Суперсингулярная кривая

• Несуперсингулярная кривая

Особое удобство суперсингулярных эллиптических кривых в том, что для них легко вычислить порядок, в то время как вычисление порядка несуперсингулярных кривых вызывает трудности. Суперсингулярные кривые особенно удобны для создания самодельной ЕСС-криптосистемы. Для их использования можно обойтись без трудоёмкой процедуры вычисления порядка.

Проективные координаты[править | править исходный текст]

Для вычисления суммы пары точек на эллиптической кривой требуется не только несколько операций сложения и умножения в , но и операция обращения, то есть для заданного  нахождение такого , что , которая на один-два порядка медленнее, чем умножение. К счастью, точки на эллиптической кривой могут быть представлены в различных системах координат, которые не требуют использования обращения при сложении точек:

• в проективной системе координат каждая точка  представляется тремя координатами , которые удовлетворяют соотношениям:

, .

• в системе координат Якоби точка также представляется тремя координатами  с соотношениями: , .

• в системе координат López-Dahab выполняется соотношение: , .

• в модифицированной системе координат Якоби используются 4 координаты  с теми же соотношениями.

• в системе координат Чудновского-Якоби используется 5 координат .

Важно отметить, что могут существовать различные именования — например, IEEE P1363-2000 называет проективными координатами то, что обычно называют координатами Якоби.

Реализация шифрования[править | править исходный текст]

Конкретные реализации алгоритмов шифрования на эллиптической кривой описаны ниже. Здесь мы рассмотрим общие принципы эллиптической криптографии.

Набор параметров[править | править исходный текст]

Для использования эллиптической криптографии все участники должны согласовать все параметры, определяющие эллиптическую кривую, т.е. набор параметров криптографического протокола. Эллиптическая кривая определяется константами  и  из уравнения (2). Абелева подгруппа точек является циклической и задается одной порождающей точкой G. При этом кофактор , где n — порядок точки G, должен быть небольшим (, желательно даже ).

Итак, для поля характеристики 2 набор параметров: , а для конечного поля , где , набор параметров: .

Существует несколько рекомендованных наборов параметров:

• NIST^[2]

• SECG^[3]

Для создания собственного набора параметров необходимо:

1. Выбрать набор параметров.

2. Найти эллиптическую кривую, удовлетворяющую этому набору параметров.

Для нахождения кривой для заданного набора параметров используются два метода:

• Выбрать случайную кривую, затем воспользоваться алгоритмом подсчета точек.^[4][5]

• Выбрать точки, после чего построить кривую по этим точкам, используя технику умножения.

Существует несколько классов криптографически «слабых» кривых, которых следует избегать:

• Кривые над 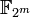, где  - не простое число. Шифрование на этих кривых подвержено атакам Вейля.

• Кривые с 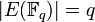 уязвимы для атаки, которая отображает точки данной кривой в аддитивную группу поля .

Быстрая редукция (NIST-кривые)[править | править исходный текст]

Деление по модулю p (которое необходимо для операций сложения и умножения) могут выполняться быстрее, если в качестве p выбрать простое число близкое к степени числа 2. В частности, в роли p может выступать простое число Мерсенна. Например, хорошим выбором являются  или . Национальный институт стандартов и технологий (NIST) рекомендует использовать подобные простые числа в качестве p.

Ещё одним преимуществом кривых, рекомендованных NIST, является выбор значения , что ускоряет операцию сложения в координатах Якоби.

Эллиптические кривые, рекомендованные NIST[править | править исходный текст]

NIST рекомендует 15 эллиптических кривых. В частности, FIPS 186-3 рекомендует 10 конечных полей. Некоторые из них:

• поля , где простое p имеет длину 192, 224, 256, 384 или 521 битов.

• поля , где m = 163, 233, 283, 409 или 571.

Причем для каждого конечного поля рекомендуется одна эллиптическая кривая. Эти конечные поля и эллиптические кривые выбраны из-за высокого уровня безопасности и эффективности программной реализации.

Размер ключа[править | править исходный текст]

Самым быстрым алгоритмам, решающим задачу дискретного логарифмирования на эллиптических кривых, таким как алгоритм Шенкса и ρ-метод Полларда, необходимо операций. Поэтому размер поля должен как минимум в два раза превосходить размер ключа. Например, для 128-битного ключа рекомендуется использовать эллиптическую кривую над полем , где p имеет длину 256 битов.

Самые сложные схемы на эллиптических кривых, публично взломанные к настоящему времени, содержали 112-битный ключ для конечного простого поля и 109-битный ключ для конечного поля характеристики 2. В июле 2009 года, кластер из более чем 200 Sony Playstation 3 за 3.5 месяца нашел 109-битный ключ. Ключ над полем характеристики 2 был найден в апреле 2004 года, с использованием 2600 компьютеров, в течение 17 месяцев.

Приложения[править | править исходный текст]

Большинство криптосистем современной криптографии естественным образом можно "переложить" на эллиптические кривые. Основная идея заключается в том, что известный алгоритм, используемый для конкретных конечных групп переписывается для использования групп рациональных точек эллиптических кривых:

• ECDSA алгоритм, основывающийся на ЭЦП.

• ECDH алгоритм, основывающийся на алгоритме Диффи — Хеллмана.

• ECMQV алгоритм, основывающийся на MQV, протоколе распределения ключей Менезеса-Кью-Венстоуна.

• ‎ГОСТ Р 34.10-2012

• Факторизация Ленстры с помощью эллиптических кривых

• Dual EC DRBG

Необходимо отметить, что безопасность таких систем цифровой подписи опирается не только на криптостойкость алгоритмов шифрования, но и на криптостойкость используемыхкриптографических хэш-функций и генераторов случайных чисел.