
Логические задачи
1. По обвинению в ограблении перед судом предстали Иванов, Петров, Сидоров. Следствием установлено следующее:
1) Если Иванов не виновен или Петров виновен, то Сидоров виновен.
2) Если Иванов не виновен, то Сидоров не виновен.
Виновен ли Иванов?
2. Виктор, Роман, Юрий и Сергей заняли на математической олимпиаде первые четыре места. Когда их спросили о распределении мест, они дали три таких ответа:
1) Сергей - первый, Роман - второй;
2) Сергей - второй, Виктор - третий;
3) Юрий - второй, Виктор - четвертый.
Как распределились места, если в каждом ответе только одно утверждение истинно?
3. Приведите рассуждения и представьте ответ на поставленный вопрос:
Узнику предложены на выбор три комнаты, в одной из которых находилась принцесса, а в двух других сидели тигры. На дверях комнат были вывешены таблицы со следующими надписями:
|
I |
II |
III |
|
В этой комнате сидит тигр |
В этой комнате находится принцесса |
Тигр сидит в комнате II |
Король сообщил узнику, что одно из этих утверждений является истинным. В какой по номеру комнате находится принцесса?
4. Приведите рассуждения и дайте ответ на поставленный вопрос:
"Перед судом стоит три человека, из которых каждый может быть либо туземцем, либо колониалистом. Судья знает, что туземцы всегда отвечают на вопросы правдиво, между тем как колониалисты всегда лгут. Однако судья не знает, кто из них туземец, а кто колониалист. Он спрашивает первого, но не понимает его ответа. Поэтому он спрашивает сначала второго, а потом третьего о том, что ответил первый. Второй говорит, что первый говорил, что он туземец. Третий говорит, что первый назвал себя колониалистом. Кем были второй и третий подсудимые?"
5. Приведите рассуждения и дайте ответ на поставленный вопрос:
"На острове живут два племени: молодцы, которые всегда говорят правду, и лжецы, которые всегда лгут. Путешественник встретил туземца, спросил его, кто он такой, и, когда услышал, что он из племени молодцов, нанял его в услужение. Они пошли и увидели вдали другого туземца, и путешественник послал своего слугу спросить его, к какому племени он принадлежит. Слуга вернулся и сказал, что тот утверждает, что он из племени молодцов. Спрашивается, был ли слуга молодцом или же лгуном.
6. Приведите рассуждения и дайте ответ на поставленный вопрос.
Профессор КУКУШКА послал своим коллегам в семь стран научные труды, перепутав конверты. Чех КУКАЧКА, интересующийся орлами, получил письма на датском языке и статью о фламинго, которая была предназначена французу КУКУ. Последний получил итальянское письмо и статью о клесте, предназначенную для голландца КОКОКА, который получил испанское письмо и монографию о лазоревке, интересующую датчанина КУКЕНА, получившего статью об орлах. Итальянец КУКУЛО интересующийся пчелоедом, получил немецкое письмо, а немец КУКУК, интересующийся ласточками, - французское. Кто получил статью, предназначенную для испанца КУКИЛО, и на каком языке было написано письмо, которое КУКИЛО получил?
7. Приведите рассуждения и дайте ответ на поставленный вопрос.
Самодержавный правитель одного острова хотел воспрепятствовать тому, чтобы на острове поселились пришельцы. Желая соблюсти видимость справедливости, он издал распоряжение, согласно которому всякий, желающий поселиться на острове, должен, хорошо поразмыслив, высказать любое предложение, причем после предварительного предупреждения, что от содержания этого предложения зависит его жизнь. Распоряжение гласило: "Если пришелец скажет правду, его расстреляют. Если он скажет неправду, его повесят". Как пришелец, став жителем острова, сохранит свою жизнь?"
|
Интересные логические задачи |
|
|
|||||||||||||||||||||||||||||||||||||||
|
Испытание логики Пятеро друзей - Андрей, Борис, Виктор, Григорий и Дмитрий - решили записаться в кружок любителей логических задач. Но староста кружка предложил им вначале выдержать вступительный экзамен и поставил условия этого экзамена: — Вы будете приходить к нам в кружок каждый вечер, но все время - в разных сочетаниях. При этом вы должны будете выполнить еще целый ряд условий. Вот они.
Друзьям удалось выполнить условия старосты и стать членами кружка любителей логических задач. Сообразите, в каком порядке друзья приходили к старосте. Ответ: К старосте ребята являлись день за днем в таком составе: 1. Андрей и Дмитрий. 2. Андрей, Борис и Григорий. 3. Андрей и Борис. 4. Виктор и Григорий. 5. Борис, Виктор и Дмитрий. 6. Борис, Виктор и Григорий. 7. Борис и Виктор.
У кого живет зебра? И кто пьет воду? В один ряд стоят пять домов, покрашенных в разные цвета, - красный, белый, зеленый, голубой и оранжевый. В них живут люди разных национальностей - норвежец, испанец, австриец, англичанин и японец. Все жильцы пьют разные напитки, ездят на разных машинах и содержат у себя дома разных животных. Ваше задание - угадать, у кого из них содержится зебра. А для этого вот вам несколько подсказок.
Теперь у вас есть все данные для того, чтобы определить, владелец какого дома держит у себя зебру. Но ответ на этот вопрос ищите сами - хватит подсказок! Ответ: Лучше всего для разгадки этого задачи нарисовать сетку, где в верхней строке проставить номера домов, а в каждой левой строке прописывать следующие отгадки: цвет дома, национальность хозяина, животное, напиток, автомобильТогда рассуждение будет выглядеть следующим образом. Норвежец живет в первом доме, рядом с голубым. Следовательно, второй дом - голубой. Первый дом, вероятнее всего - оранжевый. Он не может быть красным (в красном живет англичанин), не может быть зеленым (зеленый расположен правее белого) и не может быть белым, так как правее белого дома расположен зеленый (а второй дом - голубой). В первом доме не могут пить ни какао (какао пьет австриец), ни молоко (его пьют в среднем доме), ни кофе (кофе пьют в зеленом доме). Не могут пить в первом доме и апельсиновый сок, так как пьющий апельсиновый сок ездит на «Шевроле», а в 1-м оранжевом доме ездят на машине модели «Мерседес». Итак, получается, что воду пьет норвежец, который живет в 1-м доме. Кто может быть хозяином улиток? Тот, кто ездит на «Ауди», следовательно, им не может быть хозяин 1-го дома (он ездит на «Тойоте»), не может быть хозяин 2-го дома (у него лошадь). Не может им быть хозяин 4-го дома (он ездит на «Шевроле»), ни хозяин 5-го дома (он ездит на «Ниссане»). Значит, улиток разводят в 3-м доме. Лиса, хозяин которой живет рядом с ездящим на «Форде», не может жить в 5-м доме, так как там ездят на «Шевроле». Следовательно, лиса живет в 1-м доме. А хозяин 2-го дома ездит на «Форде». В 5-м доме живет японец, в 4-м - испанец, у которого собака. Значит, зебра живет у японца, в 5-м доме. Таблица-отгадка
Яндекс.ДиректВсе объявления
Новоселы На краю города образовалась новая улица из 8 домов, в которые вселилось 8 семей: механизатора Забалуева, электрика Байдакова, геолога Гулякова, высотника Морякина, конструктора Апухтина, строителя Жмыхова, мастера Шадрина и химика Авдеева. Жмыхову, Апухтину, Авдееву и Шадрину предоставлены дома на правой стороне улицы - с нечетными номерами (1,3, 5, 7), а остальным - с четными. Угадайте, кто где поселился. Для подсказки вот вам небольшая информация.
Разгадку лучше искать, нарисовав схему расположения домов. Ответ: Вот схема расселения семей новоселов с указанием номеров их домов: 2 - Морякин. 4 - Гуляков. 6 - Байдаков. 8 - Забалуев. 1 - Авдеев. 3 - Шадрин. 5 - Жмыхов. 7 - Апухтин.
Кто когда дежурит? Семеро друзей-дружинников дежурят в своем районе по очереди всю неделю. Каждый дежурит по одному вечеру. Имена дружинников - Андрей, Борис, Григорий, Дима, Евгений, Сергей и Федор. Угадайте, кто в какой день дежурит. Для отгадки, как всегда, дается несколько подсказок.
Ответ: График дежурства выстроен следующим образом: Андрей — воскресенье, Евгений - понедельник, Борис - вторник, Дима -среда, Федор - четверг, Григорий - пятница, Сергей - суббота.
На ипподроме В заезде на ипподроме принимали участие 6 жокеев - Иванов, Петров, Борисов, Васильев, Федоров и Шевчук. На них были разноцветные камзолы - синий, красный, зеленый, желтый, лиловый, голубой. Их лошади имели клички Арбитр, Дуглас, Отважный, Наяда, Решительный и Метеор. На старте участники заезда располагались следующим образом.
Какого цвета камзолы и какая лошадь была у каждого наездника? Ответ: Вот как располагались участники забега. Борисов - голубой камзол, лошадь - Арбитр. Васильев — красный камзол, лошадь - Дуглас. Иванов - лиловый камзол, лошадь - Метеор. Петров - зеленый камзол, лошадь - Отважный. Федоров - синий камзол, лошадь - Решительный. Шевчук - желтый камзол, лошадь - Наяда.
В одном купе Поезд приближался к Байкалу. В купе одного из вагонов собралось несколько человек - 4 юноши и 2 девушки. Они направлялись на строительство нового города, про который им много рассказывал уже побывавший там Богданов. Москвич Смелов ехал в Сибирь впервые. Он, как и Суров, оказался большим любителем шахмат. Одна из девушек - Нина - ехала на стройку после окончания техникума. Она была женой Валентина. У другой девушки фамилия была точно такая же, как у Михаила, а имя - такое же, как у Сурова. Лазарев и Суров были из Ленинграда, а Василий - из Ярославля. В фамилии Валентина три гласных буквы, а Валерий очень любит музыку. Попробуйте установить имена и фамилии будущих новоселов. Ответ: Вот имена и фамилии будущих новоселов. Василий Богданов, Валентин Лазарев, Михаил Смелов, Валерий Суров, Нина Лазарева и Валерия Смелова.
Угадай фамилию В поезде рейсом «Санкт-Петербург - Москва» едут три пассажира, фамилии которых - Иванов, Петров и Сидоров. Точно такие же фамилии имеют машинист, кочегар и кондуктор поездной бригады. Попробуйте отгадать фамилию машиниста поезда. Для этого - несколько подсказок.
Ответ: Известно, что кондуктор живет точно на полпути от Москвы до Санкт-Петербурга. (Об этом упоминается в пункте 2.) Один пассажир живет в Москве (1), другой в Санкт-Петербурге (3). Значит, ни тот, ни другой не могут считаться близкими соседями кондуктора. Значит, ближайшие соседи кондуктора - не Иванов и не Петров (поскольку упомянуто, что его месячный заработок не делится на три), а Сидоров. То есть получается, кондуктор - не Сидоров и кочегар - не Сидоров. Значит, Сидоров - машинист. Тогда кондуктор - Петров, кочегар - Иванов. |
Метод первый: Метод рассуждений
|
|
Способ рассуждений - самый примитивный способ. Этим способом решаются самые простые логические задачи. Его идея состоит в том, что мы проводим рассуждения, используя последовательно все условия задачи, и приходим к выводу, который и будет являться ответом задачи. Часто решение ведется методом от противного. |
Задача 1. Вадим, Сергей и Михаил изучают различные иностранные языки: китайский, японский и арабский. На вопрос, какой язык изучает каждый из них, один ответил: "Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский". Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из молодых людей? Решение. Имеется три утверждения. Если верно первое утверждение, то верно и второе, так как юноши изучают разные языки. Это противоречит условию задачи, поэтому первое утверждение ложно. Если верно второе утверждение, то первое и третье должны быть ложны. При этом получается, что никто не изучает китайский. Это противоречит условию, поэтому второе утверждение тоже ложно. Остается считать верным третье. ^
Метод второй: Алгебраический метод
|
|
Так, например, при применении алгебраического метода наиболее трудным является перевод текста задачи на язык формул. Далее, если вы знаете, логические законы и правила упрощения выражений, решение задачи сводится к формальным преобразованиям и приводит сразу к ответу, который остается лишь расшифровать, исходя из принятых вами обозначений. Для того чтобы решать задачи этим методом, надо знать не только основные логические законы, но и уметь их применять, а также правильно составлять тождественно истинные высказывания. |
|
Задача 2. В одной стране жили рыцари, которые всегда говорили правду, только правду и ничего кроме правды, и лжецы, которые всегда лгали. Однажды в страну проник шпион по имени Мердок, который, как и всякий шпион, иногда говорил правду, иногда лгал, в зависимости от того, что ему было выгодно. Шпион поселился с двумя жителями страны - рыцарем и лжецом. Всех троих арестовали в один день и привели на допрос. Никто не знал, кто из них кто. Они сделали следующие заявления: А сказал: Я - Мердок. В сказал: А говорит правду. С сказал: Я не Мердок. ^ Кто же из них шпион - А, В или С ? |
|
|
Решение. Введем следующие переменные: Пусть Аш =А-шпион, тогда ¯Aш =А - не шпион. Пусть Вш =В-шпион, тогда ¯Bш = В- не шпион. Пусть Cш =С-шпион, тогда ¯Cш = C- не шпион. В наших обозначениях высказывания А, В, С записываются так: А= Аш ;В= Аш ;С=¯Cш . По условиям задачи ясно, что из трёх высказываний истинным может быть либо одно (если шпион лжет), либо два ( если шпион говорит правду). Следовательно, возможны следующие варианты распределения истинных (И) и ложных (Л) высказываний: ИИЛ V ИЛИ V ЛИИ V ЛЛИ V ЛИЛ V ИЛЛ=1.(*) Посмотрим, что означает ИИЛ для введенных нами обозначений. Высказывание пленника А истинно, следовательно, Аш =1; высказывание пленника В истинно, следовательно, Аш =1; высказывание пленника С ложно, следовательно, Сш=1. То есть Аш &Аш &Сш =1. Но А и С не могут одновременно быть шпионами, следовательно, это неверно и данная конъюнкция ложна. Аналогично вариант ИЛИ "переводится" в наши обозначения так: Аш &¯Аш &¯Сш =1. Эта конъюнкция тоже ложна, поскольку А не может одновременно быть шпионом и не быть им. Интерпретируем полностью формулу (*), опуская для кратности знак конъюнкции: Аш Аш Сш U Аш ¯Аш ¯Cш U ¯Аш Аш ¯Cш U ¯Аш ¯Аш ¯Cш U ¯Аш Аш Cш U Аш ¯Аш Cш = 0 U 0 U 0 U ¯Аш ¯Cш U 0 U 0= ¯Аш ¯Cш =1. То есть ни А ни С не шпионы, следовательно, шпион v В. далее уже просто сделать вывод, что А - лжец, С - рыцарь. |
|
^
Метод третий: Метод таблиц
|
|
Основной прием, который используется при решении текстовых логических задач, заключается в построении таблиц. Таблицы не только позволяют наглядно представить условие задачи или ее ответ, но в значительной степени помогают делать правильные логические выводы в ходе решения задачи. |
|
||
|
|
Задача 3. Три клоуна Бим, Бам и Бом вышли на арену в красной, зеленой и синей рубашках. Их туфли были тех же цветов. У Бима цвета рубашки и туфель совпадали. У Бома ни туфли, ни рубашка не были красными. Бам был в зеленых туфлях, а в рубашке другого цвета. Как были одеты клоуны? |
|||
|
|
Решение. Составим таблицу, в столбцах которой отметим возможные цвета рубашек и туфель клоунов (буквами К, З и С обозначены красный, зеленый и синий цвета). Будем заполнять таблицу, используя условия задачи. Туфли Бама зеленые, а рубашка не является зеленой. Ставим знак + в клетку 2-й строки и 5-го столбца, и знак - в клетку 2-й строки и 2-го столбца. Следовательно, у Бима и Бома туфли уже не могут быть зелеными, так же как не могут быть туфли Бама синими или красными. Отметим все это в таблице (см. табл. 1). |
|
||
|
|
Далее, туфли и рубашка Бома не являются красными, отметим соответствующие ячейки таблицы знаком – . Из таблицы, заполненной на этом этапе, видим, что красные туфли могут быть только у Бима, а, следовательно, туфли Бома - синие. Правая часть таблицы заполнена, мы установили цвета обуви клоунов (табл.1). Цвет рубашки Бима совпадает с цветом его туфель и является красным. Теперь легко устанавливается владелец зеленой рубашки - Бом. Бам, в таком случае, одет в рубашку синего цвета. |
|
||
|
|
Мы полностью заполнили таблицу, в которой однозначно устанавливаются цвета туфель и рубашек клоунов (см. табл. 2) Ответ: Бим одет в красную рубашку и красные туфли, Бам в синей рубашке и зеленых туфлях, Бом в зеленой рубашке и туфлях синего цвета. |
|||
^
Метод четвёртый: Метод кругов Эйлера-Венна
|
|
Задачи, которые можно решить с помощью кругов Эйлера нельзя решить иначе, по сравнению с табличным методом или при помощи графов. Этот способ решать задачи придумал в XVIII в. великий Леонард Эйлер. |
|
|
Метод диаграмм Эйлера-Венна позволяет графически решать математические задачи на основе применения теории множеств. Этот метод прост, если в нем разобраться. |
||
|
Диаграммы Эйлера-Венна могу быть построены по-разному. Рассмотрим три простейших случая. а) Дано некоторое множество и указано свойство ^ Х. Очевидно, элементы данного множества могут обладать или не обладать свойством Х. Поэтому данное множество распадается на две части: А - множество элементов, обладающих свойством Х; В множество элементов, не обладающих свойством Х. б) Дано некоторое множество и указаны два свойства: Х и У. Так как элементы данного множества могут обладать или не обладать каждым из этих свойств, то возможны четыре случая: ^ А - элементы обладают Х и У; В - элементы обладают Х и не обладают У; С - элементы не обладают Х и не обладают У; D - элементы не обладают Х и обладают У. в) Дано некоторое множество и указаны три свойства: X, Y и Z. В этом случае данное множество распадается на восемь частей. Если будет указано пять свойств, то множество распадется на 32 части, диаграммы станут еще более сложными. Итак, с увеличением свойств число частей каждый раз увеличивается. Некоторые части могут оказаться пустыми: в них не попадет ни один элемент множества. |
|
|
|
|
||
|
|
||
|
Задача 4. Из сотрудников фирмы 16 побывали во Франции,10-в Италии,6-в Англии; в Англии и Италии-5; в Англии и Франции -6; во всех трех странах - 5 сотрудников. Сколько человек посетили и Италию, и Францию, если всего в фирме работают 19 человек, и каждый из них побывал хотя бы в одной из названных стран? |
||
|
|
Решение. Нам известно, что во всех трех странах было 5 сотрудников. В Англии и Италии тоже 5, значит эти же сотрудники были и во Франции и поэтому в пересечении кругов А и И ставим 0. В Франции и Италии нам неизвестно поэтому пишем х-5 в пересечении кругов А и Ф. Т.к. в Англии было 6 человек, то 6-5-1=0 пишем 0,во Франции 16-х+5-6 и Италии 10-х+5-5 и всего в фирме 19 сотрудников, то остается составить и решить уравнение: 1+16-х+5-6+5+х-5+10-х+5-5=19, отсюда х=7, значит в Италии и Франции побывало 7-5=2 сотрудника фирмы. |
|
^
Метод пятый: Метод графов
|
Графом
называют схему, в которой обозначаются
только наличие объектов (элементов
системы) и наличие и вид связи между
объектами.
Объекты представляются
в графе вершинами (на схеме они
обозначаются кружочками, прямоугольниками
и т.п.). Связи между объектами
представляются, если связь однонаправленная
(обозначается на схеме линиями со
стрелками) или ребрами, если связь
между объектами двусторонняя
(обозначается на схеме линиями без
стрелок).
Например, если нужно
представить в графе, что из состояния
А в состояние В возможен переход под
воздействием V, то это можно изобразить
так:
|
|
Задача 5. Марина, Лариса, Жанна и Катя умеют играть на разных инструментах (пианино, виолончели, гитаре, скрипке), но каждая только на одном. Они же знают иностранные языки (английский, французский, немецкий и испанский), но каждая только один. Известно:
Кто на каком инструменте играет и какой иностранный язык знает? |
|
|
^
Метод шестой: Метод блок-схем
|
|
В этом разделе рассматривается еще один тип логических задач. Это задачи, в которых с помощью сосудов известных емкостей требуется отмерить некоторое количество жидкости, а также задачи, связанные с операцией взвешивания на чашечных весах. Простейший прием решения задач этого класса состоит в переборе возможных вариантов. Понятно, что такой метод решения не совсем удачный, в нем трудно выделить какой-либо общий подход к решению других подобных задач |
|
|||
|
Более систематический подход к решению задач "на переливание" заключается в использовании блок-схем. Суть этого метода состоит в следующем. Сначала выделяются операции, которые позволяют нам точно отмерять жидкость. Эти операции называются командами. Затем устанавливается последовательность выполнения выделенных команд. Эта последовательность оформляется в виде схемы. Подобные схемы называются блок-схемами и широко используются в программировании. Составленная блок-схема является программой, выполнение которой может привести нас к решению поставленной задачи. Для этого достаточно отмечать, какие количества жидкости удается получить при работе составленной программы. При этом обычно заполняют отдельную таблицу, в которую заносят количество жидкости в каждом из имеющихся сосудов. |
|
||||
|
|
Задача 6. Имеются два сосуда — трехлитровый и пятилитровый. Нужно, пользуясь этими сосудами, получить 1, 2, 3, 4, 5, 6, 7 и 8 литров воды. В нашем распоряжении водопроводный кран и раковина, куда можно выливать воду. |
||||
|
|
|
Решение. Перечислим все возможные операции, которые могут быть использованы нами, и введем для них следующие сокращенные обозначения: НБ — наполнить больший сосуд водой из-под крана; НМ — наполнить меньший сосуд водой из-под крана; ОБ — опорожнить больший сосуд, вылив воду в раковину; ОМ — опорожнить меньший сосуд, вылив воду в раковину; Б→М — перелить из большего в меньший, пока больший сосуд не опустеет или меньший сосуд не наполнится; М→Б — перелить из меньшего в больший, пока меньший сосуд не опустеет или больший сосуд не наполнится. Выделим среди перечисленных команд только три: НБ, Б→М, ОМ. Кроме этих трех команд рассмотрим еще две вспомогательные команды: Б = 0 ? — посмотреть, пуст ли больший сосуд; М = З ? — посмотреть, наполнен ли малый сосуд. В зависимости от результатов этого осмотра мы переходим к выполнению следующей команды по одному из двух ключей - "да" или "нет". Такие команды в программировании принято называть командами "условного перехода" и изображать в блок-схемах в виде ромбика с двумя ключами-выходами. Договоримся теперь о последовательности выполнения выделенных команд. После Б→М будем выполнять ОМ всякий раз, как меньший сосуд оказывается наполненным, и НБ всякий раз, как больший сосуд будет опорожнен. Последовательность команд изобразим в виде блок-схемы (Рис. 1). Начнем выполнение программы. Будем фиксировать, как меняется количество воды в сосудах, если действовать по приведенной схеме. Результаты оформим в виде таблицы (табл.) |
|||
|
|
|
||||
|
|
Задача 7. Среди четырех монет одна фальшивая. Она отличается массой, однако неизвестно, легче она или тяжелее. Масса настоящей монеты 5 г. Как при помощи двух взвешиваний на чашечных весах обнаружить фальшивую монету, если имеется одна гиря массой 5 г? Можно ли при этих условиях опознать, легче фальшивая монета или тяжелее? |
||||
|
|
|
Решение. Пусть m1, m2, m3, m4 – массы четырех монет соответственно, Г - масса гири. Оформим решение в виде блок-схемы (см. рис.). Приведенная схема задает программу, осуществление которой позволяет установить фальшивую монету и определить, легче она или тяжелее. Взвешиваниям в блок-схеме соответствуют прямоугольники - операторы условного перехода. В схеме выделены первое и второе взвешивания горизонтальными линиями. |
|||
|
|
|
||||
^
Метод седьмой: Метод математического бильярда
|
|
Надеемся, что Вам известна игра бильярд за прямоугольным столом с лузами. Появившись до нашей эры в Индии и Китае, бильярд через много веков перекочевал в европейские страны – упоминание о нем имеется в английских летописях VI века. В России бильярд стал известен и распространился при Петре I. |
|
|
Подобно тому, как азартная игра в кости вызвала к жизни "исчисление" вероятностей, игра в бильярд послужила предметом серьезных научных исследований по механике и математике. Представьте себе горизонтальный бильярдный стол произвольной формы, но без луз. По этому столу без трения движется точечный шар, абсолютно упруго отражаясь от бортов стола. Спрашивается, какой может быть траектория этого шарика? Поиски ответа на этот вопрос и послужили появлению теории математического бильярда или теории траекторий. |
||
|
Задачи на переливание жидкостей можно очень легко решать, вычерчивая бильярдную траекторию шара, отражающегося от бортов стола, имеющего форму параллелограмма. Рассмотрим туже задачу, что и в предыдущем разделе (Метод блок-схем). Задача 8. Имеются два сосуда — трехлитровый и пятилитровый. Нужно, пользуясь этими сосудами, получить 1, 2, 3, 4, 5, 6, 7 и 8 литров воды. В нашем распоряжении водопроводный кран и раковина, куда можно выливать воду. |
||
|
|
Решение. В рассматриваемой задаче стороны параллелограмма должны иметь длины 3 и 5 единиц. По горизонтали будем откладывать количество воды в литрах в 5-литровом сосуде, а по вертикали – в 3-литровом сосуде. На всем параллелограмме нанесена сетка из одинаковых равносторонних треугольников (см. рис.1) |
|
|
|
||
|
Бильярдный шар может перемещаться только вдоль прямых, образующих сетку на параллелограмме. После удара о стороны параллелограмма шар отражается и продолжает движение вдоль выходящего из точки борта, где произошло соударение. При этом каждая точка параллелограмма, в которой происходит соударение, полностью характеризует, сколько воды находится в каждом из сосудов. Пусть шар находится в левом нижнем углу и после удара начнет перемещаться вверх вдоль левой боковой стороны параллелограмма до тех пор, пока не достигнет верхней стороны в точке А. Это означает, что мы полностью наполнили водой малый сосуд. Отразившись упруго, шар покатится вправо вниз и ударится о нижний борт в точке В, координаты которой 3 по горизонтали и 0 по вертикали. Это означает, что в большом сосуде 3 литра воды, а в малом сосуде воды нет, то есть мы перелили воду из малого сосуда в большой сосуд. Прослеживая дальнейший путь шара, и записывая все этапы его движения в виде отдельной таблицы (табл.1), в конце концов, мы попадаем в точку Н, которая соответствует состоянию, когда малый сосуд пуст, а в большом сосуде 4 литра воды. Таким образом, получен ответ и указана последовательность переливаний, позволяющих отмерить 4 литра воды. Все 8 переливаний изображены схематически в таблице. Является ли это решение самым коротким? Нет, существует второй путь, когда воду сначала наливают в пятилитровый сосуд. Если на диаграмме шар из точки О покатится вправо по нижней стороне параллелограмма и затем, отразившись от правой боковой стороны, в точку 2 на верхней стороне параллелограмма и т.д., то получим более короткое решение задачи. Можно показать, что полученное решение с 6 переливаниями уже является самым коротким. |
||
^
Копилка интересных задач
-
Левин, Митерев, Набатов работают в банке, в качестве бухгалтера, кассира и экономиста. Если Набатов – экономист, то Митерев – бухгалтер. Если Митерев - не кассир, то Левин – не экономист. Если Левин – бухгалтер, то Набатов – экономист. Кто какую должность занимает?
-
В соревнованиях по гимнастике участвуют: Аня, Валя, Таня и Даша. Болельщики строят прогнозы: 1) Таня займет I место, Валя - II; 2) Таня займет II место, Даша - III; 3) Аня займет II место, Даша - IV. По окончании соревнований оказалось, что в каждом предположении только одно из высказываний каждого болельщика истинно, другое - ложно. Каковы результаты соревнований, если на каждом месте по одной девушке?
-
Незнайка услышал разговор Сиропчика, Пилюлькина, Торопыжки и Знайки. Известно, что каждый из них либо всегда лжет, либо всегда говорит правду. 1) Сиропчик обвинил Пилюлькина в том, что он – лгун. 2) Знайка сказал Сиропчику: «Сам ты лгун!». 3) Торопыжка заметил: «Оба они лгуны». 4) Знайка спросил у Звезды «А я?». 5) На что Торопыжка ответил «И ты тоже лгун!» «Кто же из них говорит правду?» - удивился Незнайка. Помогите ему.
-
Три друга обсуждали историю Нового года и каждый сказал следующее: 1) Празднование Нового года с 1 января установили во Франции в 45 году до Рождества Христова (Юлием Цезарем). 2) Празднование Нового года с 1 января установили римляне в 1659 году указом Карла IX. 3) Празднование Нового года с 1 января установили во II веке и не французы. Оказавшийся рядом знаток истории сказал, что каждый из них прав только в одном из двух высказанных предложений. Где и в какое время было установлено празднование Нового года с 1 января?
-
В классе 36 человек. 18 человек посещают математический кружок, 14 физический, 10 химический, 2 человека посещают все три кружка, 8 – математический и физический, 5 – математический и химический, 3 - физический и химический кружки. Сколько учеников класса не посещают никаких кружков?
-
На соревнованиях по легкой атлетике Андрей, Боря, Сережа и Володя заняли первые четыре места. Но когда девочки стали вспоминать, как эти места распределились между победителями, то мнения разошлись: Даша: Андрей был первым, а Володя – вторым Галя: Андрей был вторым, а Борис – третьим Лена: Боря был четвертым, а Сережа вторым Ася: каждая девочка сделало одно правильное и одно неправильное заявление
-
Как из полного сосуда ёмкостью в 12 л отлить половину, пользуясь двумя пустыми сосудами ёмкостью в 8 и 5 л?
-
Среди 101 одинаковых по виду монет одна фальшивая, отличающаяся по весу. Как с помощью чашечных весов без гирь за два взвешивания определить, легче или тяжелее фальшивая монета? Находить фальшивую монету не требуется.
-
Условия задачи. 1. Есть 5 домов каждый разного цвета. 2. В каждом доме живет один человек, отличающийся от соседнего по национальности: немец, англичанин, швед, датчанин, норвежец. 3. Каждый пьет только один определенный напиток, курит определенную марку сигарет и держит определенное животное. 4. Никто из 5 человек не пьет одинаковые с другими напитки, не курит одинаковые сигареты и не держит одинаковое животное. Вопрос: кому принадлежит рыба? Подсказки: 1. Англичанин живет в красном доме. 2. Швед держит собаку. 3. Датчанин пьет чай. 4. Зеленый дом стоит слева от белого. 5. Жилец зеленого дома пьет кофе. 6. Человек, который курит Pall Mall, держит птицу. 7. Жилец из среднего дома пьет молоко. 8. Жилец из желтого дома курит Dunhill. 9. Норвежец живет в первом доме. 10. Курильщик Marlboro живет около того, кто держит кошку. 11. Человек, который держит лошадь, живет около того, кто курит Dunhill. 12. Курильщик сигарет Winfield пьет пиво. 13. Норвежец живет около голубого дома. 14. Немец курит Rothmans. 15. Курильщик Marlboro живет по соседству с человеком, который пьет воду.


 Схема
решения логических задач:
Схема
решения логических задач:








 Если
нужно представить, что к-тый участник
соревнования занял n-е место (или, что
то же самое, n-е место занял к-тым
участником), это можно изобразить
так:
Если
нужно представить, что к-тый участник
соревнования занял n-е место (или, что
то же самое, n-е место занял к-тым
участником), это можно изобразить
так:

 Из
пятого условия, что Жанна знает
французский язык, рисуем стрелку. Из
третьего условия, что Марина не знает
ни немецкого, ни английского, а
французский знает Жанна, то Марина
знает испанский и, рассматривая первое
условие она играет на гитаре. Из условия
№2 видим, что Лариса играет на пианино,
т.к. Марина играет на гитаре, а на других
инструментах она играть не умеет, и
значит, она говорит по-немецки.
Из
пятого условия, что Жанна знает
французский язык, рисуем стрелку. Из
третьего условия, что Марина не знает
ни немецкого, ни английского, а
французский знает Жанна, то Марина
знает испанский и, рассматривая первое
условие она играет на гитаре. Из условия
№2 видим, что Лариса играет на пианино,
т.к. Марина играет на гитаре, а на других
инструментах она играть не умеет, и
значит, она говорит по-немецки.
 Т.к.
Жанна не играет на скрипке, то остается
один инструмент, на котором она может
играть это виолончель. Тогда Катя
играет на скрипке, и знает английский
язык.
Т.к.
Жанна не играет на скрипке, то остается
один инструмент, на котором она может
играть это виолончель. Тогда Катя
играет на скрипке, и знает английский
язык.

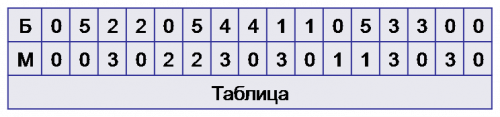 Дальше
эта последовательность будет полностью
повторяться. Из таблицы видим, что
количество воды в обоих сосудах вместе
образует следующую последовательность:
0, 5, 2, 7, 4, 1, 6, 3, 0 и т.д. Таким образом,
действуя по приведенной схеме, можно
отмерить любое количество литров от
1 до 7. Чтобы отмерить еще и 8 литров,
надо наполнить оба сосуда.
Дальше
эта последовательность будет полностью
повторяться. Из таблицы видим, что
количество воды в обоих сосудах вместе
образует следующую последовательность:
0, 5, 2, 7, 4, 1, 6, 3, 0 и т.д. Таким образом,
действуя по приведенной схеме, можно
отмерить любое количество литров от
1 до 7. Чтобы отмерить еще и 8 литров,
надо наполнить оба сосуда.
 Прокомментируем
для примера ход рассуждений, двигаясь
лишь по одной ветви блок-схемы. Итак,
первое взвешивание: пусть m1 + m2 < m3 +
+ Г. Это означает, что фальшивая монета
находится среди первых трех монет, и,
следовательно, четвертая монета
истинная, то есть m4 = 5.
Второе
взвешивание: пусть m1+m3 > m4+Г. Тогда
фальшивая монета тяжелее (так как m4+Г
- вес двух истинных монет) и это либо
первая, либо третья монета. Но показания
весов при первом взвешивании (m1+m2 <
m3+Г) позволяют нам сделать вывод, что
более тяжелой является третья монета.
Если бы показания весов при втором
взвешивании были противоположными,
то фальшивая монета должна бы быть
более легкой, а, стало быть, это была
первая монета. Наконец, если при втором
взвешивании весы будут в равновесии,
то и третья и первая монеты не могут
быть фальшивыми. Следовательно,
фальшивой является вторая монета и
вес ее меньше 5 грамм.
Прокомментируем
для примера ход рассуждений, двигаясь
лишь по одной ветви блок-схемы. Итак,
первое взвешивание: пусть m1 + m2 < m3 +
+ Г. Это означает, что фальшивая монета
находится среди первых трех монет, и,
следовательно, четвертая монета
истинная, то есть m4 = 5.
Второе
взвешивание: пусть m1+m3 > m4+Г. Тогда
фальшивая монета тяжелее (так как m4+Г
- вес двух истинных монет) и это либо
первая, либо третья монета. Но показания
весов при первом взвешивании (m1+m2 <
m3+Г) позволяют нам сделать вывод, что
более тяжелой является третья монета.
Если бы показания весов при втором
взвешивании были противоположными,
то фальшивая монета должна бы быть
более легкой, а, стало быть, это была
первая монета. Наконец, если при втором
взвешивании весы будут в равновесии,
то и третья и первая монеты не могут
быть фальшивыми. Следовательно,
фальшивой является вторая монета и
вес ее меньше 5 грамм.

