1 курс / KOMPLEKSNYE_ChISLA_korni

9

Извлечение корня из комплексного числа в тригонометрической форме

(Лекция)

Применяя формулу Муавра

,

легко найти комплексные корни n-й степени из произвольного отличного от нуля комплексного числа z .

Пусть . Тогда

uⁿ = z (1)

и все корни n-й степени из числа z являются решениями уравнения (1).

Поскольку комплексное число u отлично от нуля (в противном случае комплексное число z равно нулю, а мы договорились не рассматривать этот случай в виду того, что при z = 0 уравнение (1) имеет единственный n-кратный корень u = 0). Его можно представить в тригонометрической форме:

u = r₁ (cos φ₁ + i sin φ₁) .

Пусть, как обычно,

z = r (cos φ + i sin φ) ,

тогда уравнение (1) примет вид:

r₁ⁿ (cos nφ₁ + i sin nφ₁) = r (cos φ + i sin φ) .

Комплексные числа, заданные в тригонометрической форме равны тогда и только тогда, когда равны их модули, а аргументы отличаются на 2πk (k Z) . Поэтому

Откуда получаем:

, (k Z) .

Здесь − арифметический корень из положительного действительного числа r.

Обозначим k-й корень n-й степени из комплексного числа z через u_k . Тогда

,

где k Z , k = 0, 1, 2, 3, … , n −1 .

Замечание. Корней n-й степени из ненулевого комплексного числа z , заданного в тригонометрической форме, будет ровно n , так как именно столько различных значений будет принимать дробь , где k пробегает n значений от 0 до n-1.

Пример. Найдите .

Решение. − i = cos + i sin .

Следовательно,

Таким образом,

Точки u₀(0 ; 1) , u₁ и u₂ являются вершинами правильного треугольника (см. рис. 1).

u₀

у

Замечание. Для любого отличного от нуля комплексного числа z и любого натурального числа

u₁

u₂

0

x

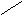
Рис. 1

n > 2 корни степени n из числа z являются вершинами правильного n - угольника с центром в точке О (0;0). Это следует из того, что модули всех корней n-й степени равны , а углы между соседними корнями u_k и

u_k+1 равны .

Действия над комплексными числами в тригонометрической форме

(Практика)

Задача 1. Используя тригонометрическую форму комплексного числа, произведите указанные действия:

а) ; б).

Решение. а) Представим сначала каждое из чисел в тригонометрической форме:

;

;

.

Поэтому

б) В данном случае первый из двух сомножителей уже представлен в тригонометрической форме. Относительно второго сомножителя этого сказать нельзя, так как здесь в скобках перед синусом стоит знак минус вместо нужного нам знака плюс. Поэтому представим сначала второй сомножитель в тригонометрической форме. Для этого мы воспользуемся четностью и нечетностью тригонометрических функций косинуса и синуса соответственно:

cos (−φ) = cos (φ) ; sin (−φ) = −sin (φ) .

Тогда можно записать :

.

Следовательно,

.

Ответ: a) 2+2i ; б) . Задача 2 . Вычислите: .

Решение. Воспользуемся формулой Муавра:

.

По этой формуле:

.

Следовательно,

Ответ : - 65 .

Задача 3. Вычислите все значения и изобразите их на комплексной плоскости.

Решение. Как известно, корень n-й степени из комплексного числа z = r (cos φ + i sin φ) имеет n различных значений, которые находятся по формуле:

= ,

где k Z , k = 0, 1, 2, 3, … , n −1 .

Представим число (−4) в тригонометрической форме:

−4 = 4 (cos π + i sin π) .

Тогда

где k = 0, 1, 2, 3.

Получаем следующие четыре значения корня четвертой степени из числа (−4):

;

;

.

у

z₀

z₁

х

0

z₂

z₃

Самостоятельная работа

1. Запишите в тригонометрической форме следующие комплексные числа:

а) z = + i ; б) z = 3+ 4 i;

в)

2) Зная, что z₁ = + i , z₂ = − sin + cos, вычислите:

а) (z_1*z₂)⁸ ; б) .

3) Вычислить все значения корней:

а)

б)

в)