Метод указ по МО

-52 -

x(k) x(k 1) L 1 2(x(k 1) )13 b(b(x(k 1) )1 c(x(k 1) )2 ) p / 2 ,

где | x(0) | r и

L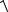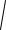192 max(1, a2 )r2 24 max(| b |4,| c |4 ) .

Аформула метода Ньютона принимает вид

а) метод спуска;

б) метод Ньютона.

Варианты

1)f (x1, x2 ) x14 2x24 (3x1 2x2 )2 2x1 4x2

2)f (x1, x2 ) x14 x24 (2x1 3x2 )2 4x1 2x2

3)f (x1, x2 ) x14 3x24 (x1 2x2 )2 2x1 2x2

4)f (x1, x2 ) x14 4x24 (3x1 2x2 )2 6x1 2x2

5)f (x1, x2 ) x14 5x24 (x1 x2 )2 4x1 2x2

6)f (x1, x2 ) x14 x24 (4x1 3x2 )2 2x1 6x2

- 53 -

7)f (x1, x2 ) x14 6x24 (5x1 x2 )2 4x1 2x2

8)f (x1, x2 ) x14 5x24 (4x1 3x2 )2 8x1 4x2

9)f (x1, x2 ) x14 4x24 (3x1 2x2 )2 6x1 2x2

10)f (x1, x2 ) x14 3x24 (2x1 3x2 )2 4x1 4x2

11)f (x1, x2 ) x14 2x24 (3x1 4x2 )2 6x1 2x2

12)f (x1, x2 ) x14 x24 (3x1 x2 )2 8x1 2x2

13)f (x1, x2 ) x14 2x24 (3x1 2x2 )2 2x1 4x2

14)f (x1, x2 ) x14 x24 (2x1 7x2 )2 4x1 2x2

15)f (x1, x2 ) x14 3x24 (x1 2x2 )2 2x1 2x2

16)f (x1, x2 ) x14 4x24 (3x1 8x2 )2 6x1 2x2

17)f (x1, x2 ) x14 5x24 (2x1 9x2 )2 4x1 2x2

18)f (x1, x2 ) x14 x24 (4x1 3x2 )2 2x1 6x2

19)f (x1, x2 ) x14 6x24 (5x1 x2 )2 4x1 2x2

20)f (x1, x2 ) x14 5x24 (4x1 3x2 )2 8x1 4x2

21)f (x1, x2 ) x14 4x24 (7x1 3x2 )2 6x1 2x2

22)f (x1, x2 ) x14 3x24 (2x1 3x2 )2 4x1 4x2

23)f (x1, x2 ) x14 2x24 (3x1 5x2 )2 6x1 2x2

24)f (x1, x2 ) x14 x24 (3x1 7x2 )2 8x1 2x2

25)f (x1, x2 ) x14 3x24 (5x1 2x2 )2 2x1 2x2

- 54 -

§8. Простейшая задача вариационного исчисления

Простейшая задача вариационного исчисления состоит в нахождении минимума или максимума функционала

f (x) F (t, x(t), x (t)) dt

на множестве гладких функций x(t), удовлетворяющих условиям

x( ) A, x( ) B .

Решение задачи, если оно существует, будет решением уравнения Эйлера

Поэтому уравнение Эйлера называют необходимым условием экстремума.

Всякое решение x(t) уравнения Эйлера, удовлетворяющее краевым условиям

x( ) A, x( ) B , называют экстремалью простейшей вариационной

задачи. Таким образом, решение простейшей вариационной задачи следует искать среди экстремалей.

Экстремаль x0 (t) будет решением простейшей вариационной задачи,

если удовлетворяет двум условиям – усиленному условию Лежандра и условию Якоби; их называют достаточными условиями экстремума.

1. Усиленное условие Лежандра: для задачи на минимум должно

выполняться неравенство

а для задачи на максимум должно выполняться неравенство

2. Условие Якоби: существует решение u(t) уравнения Якоби

- 56 -

Проверим, выполняются ли усиленное условие Лежандра и условие Якоби:

- 57 -

Задание № 8

Найти решение простейшей вариационной задачи

x( ) A, x( ) B ,

где числа M , m, , , b, c , A, B и функция a(t) задаются, m - целое и четное, m 2, , | c | 1.

- 58 -

9)M 5, m 4, 0, 1, b 1, c 3,

A 0, B 2, a(t) 3t2 1

10)M 3, m 8, 2, 2 , b 1, c 3,

11)M 2 , m 10, 0, 4 , b 1, c 2,

A 2, B 1, a(t) 2t4

12)M 4 , m 6, 0, 2 , b 1, c 2 ,

A 0, B 3, a(t) 1 sin 2t

13)M 5, m 2, 0, , b 1, c 2,

A 2, B 0, a(t) 4 3cos t

14)M 1, m 2, 0, 1, b 1, c 2 ,

17)M 1, m 2, 0, / 2, b 3, c 3,

A 1, B 0, a(t) 1 2sin t

18)M 2, m 4, 0, 3, b 1, c 2 ,

- 59 -

21) M 6, m 2, 1, 3, b 1, c 3,

A 1, B 1, a(t) 4t2 t

22)M 5, m 2, 0, 1, b 1, c 3,

A 0, B 2, a(t) 3t2 1

23)M 3, m 10, 2, 2 , b 1, c 3,

24)M 2 , m 6, 0, 4 , b 1, c 2,

A 2, B 1, a(t) 5t2 3

25)M 4, m 8, 0, 2 , b 1, c 2 ,

A 0, B 3, a(t) 2 cos 3t

- 60 -

Библиографический список

1. Корнеенко, В. П. Методы оптимизации: учебник / В. П.

Корнеенко. – М.: Высшая школа, 2007. – 664 с.

2. Пантелеев, А.В. Методы оптимизации в примерах и задачах:

учебное пособие / А. В. Пантелеев, Т. А. Летова. – М.: Высшая школа,

2002. – 554 с.

3.Пантелеев, А. В. Вариационное исчисление в примерах и задачах. / А. В. Пантелеев. – М.: МАИ, 2000. – 228 с.

4.Васильев, Ф. П. Методы оптимизации / Ф. П. Васильев. – М.:

Наука, 2002. – 824 с.

- 61 -

Содержание