Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный педагогический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Метод указ по МО

.pdf

Скачиваний:

Добавлен:

08.06.2015

Размер:

575.04 Кб

Скачать

☆

1 / 61 2 3 4 5 6 > Следующая >>>

Министерство образования и науки Российской Федерации Вологодский государственный технический университет

Кафедра информационных систем и технологий

Методы оптимизации: примеры и задания

Методическое пособие для студентов обучающихся по направлениям

230100.62 – информатика и вычислительная техника,

230200.62 – информационные системы

Вологда 2011 г.

- 3 -

УДК 519.8

ББК 22.1

Методы оптимизации: примеры и задания: методическое пособие. –

Вологда: ВоГТУ, 2011. - 60 с.

Рассматриваются основные понятия, методы и алгоритмы решения задач по восьми разделам дисциплины методов оптимизации. По каждому разделу приведены примеры и варианты заданий для самостоятельного решения.

Предназначено для студентов, обучающихся по направлениям 230100.62 -

информатика и вычислительная техника и 230200.62 - информационные системы.

Утверждено редакционно-издательским советом ВоГТУ

Составитель: доктор физико-математических наук, профессор Наимов А.Н.

Рецензент: кандидат физико-математических наук, доцент Назимов А.Б.

- 4 -

§1. Методы решения задач линейного программирования

Задачей линейного программирования называют задачу нахождения наибольшего или наименьшего значения линейной функции, зависящей от нескольких переменных, при ограничениях заданных в виде линейных равенств и неравенств. Задача линейного программирования может быть задана в трех формах: общей, стандартной, канонической.

Задача линейного программирования в общей форме имеет следующий

вид:

f (x) c x max (min),

A x b(1) ,

A x b(2) ,

, x

где

x (x , ,

) - неизвестный

вектор-столбец,

c (c , , c

)

вектор-строка коэффициентов линейной функции

f (x) c1x1 cn xn ,

и A

- матрицы размерностей

m n и m

n соответственно,

b(1) ,

b(2)

векторы-столбцы,

p - фиксированное натуральное число не превосходящее n .

Функцию

f (x)

называют

целевой

функцией,

ограничения

A x b(1)

A x b(2)

называют прямыми

ограничениями,

x 0,

, x

непрямыми ограничениями.

В случае, когда матрица

и вектор b(2)

нулевые, A A - матрица

размерности

m n ,

b(1) b -

m-мерный вектор и

p n, получаем задачу

линейного программирования в стандартной форме:

f (x) c x max (min),

Ax b,

x ,

где - нулевой вектор.

- 5 -

Если

A ,

b(1)

равны

нулю,

b(2)

b и p n,

то получаем

задачу линейного программирования в канонической форме:

f (x) c x

max (min),

Ax b ,

x .

Задачу линейного программирования из общей формы можно привести к

стандартной, заменяя равенство

A x b(2) двумя неравенствами

A x b(2) ,

а неизвестные x , , x

заменяя новыми неизвестными

, x

x x ,

p 1

p 2

x~ ,

n 1

где n p 2(n p) , и добавляя непрямые ограничения

, , xn 0.

получим задачу

Тогда относительно неизвестного вектора x

, , x~ )

линейного программирования в стандартной форме.

Задачу линейного программирования из стандартной формы можно

привести к канонической, заменяя неравенство Ax b равенством

Ax y b,

где y - дополнительный неизвестный m–мерный вектор с неотрицательными координатами. Тогда относительно неизвестного вектора z (x, y) получим задачу линейного программирования в канонической форме. Таким образом,

все три формы равносильны.

Вектор x , удовлетворяющий прямым и непрямым ограничениям,

называют допустимым планом. А допустимый план x *, на котором достигается максимум или минимум целевой функции, называют оптимальным планом. Решить задачу линейного программирования, значит найти оптимальный план.

Рассмотрим два метода решения задач линейного программирования:

1) графический метод решения двумерной задачи линейного программирования в стандартной форме;

-6 -

2)симплекс-метод решения задачи линейного программирования любой размерности в канонической форме.

Графический метод. Пусть задана двумерная задача линейного программирования в стандартной форме:

f c1x1 c2x2 max, min ,

ak1x1 ak2x2 bk ,

k 1, m,

x1 0,

x2 0 ,

где x (x , x

) -

неизвестный

вектор, коэффициенты c ,

, a

k 2

и числа b1,

, bm известны. В этом случае множество допустимых

1, m

планов D представляет собой многоугольник (ограниченный или

неограниченный) на первой четверти координатной плоскости

OX1X2 .

Многоугольник D ограничен координатными осями и прямыми линиями

lk : ak1x1 ak2x2 bk ,

k 1, m

Графический метод состоит из следующих шагов:

1. Построим многоугольник

D -

область допустимых планов,

проведя

lk : ak1x1 ak2x2 bk ,

прямые линии

1, m

2.Находим градиент целевой функции f (c1,c2 ) .

3.Построим семейство параллельных прямых линий, перпендикулярных вектору-градиенту f (c1,c2 ) .

4.Из семейства параллельных прямых линий выделим линию, которая по

направлению вектора f (c1,c2 ) первой касается многоугольника D .

Точка касания есть точка минимума. А если нет такой линии, то точка минимума не существует.

5. Аналогично выделяется прямая линия, последней касающейся D , и

определяется точка максимума. Если такой линии нет, то точка максимума не существует.

-7 -

6.По точкам минимума и максимума, если они существуют, находим

fmin , fmax - минимум и максимум целевой функции.

Пример 1.1. Рассмотрим задачу

		f x1 10x2 max, min ,
x1 2x2 2,	3x1	10x2 30, 0,5x1 5x2 2,5, x1		0,	x2 0 .
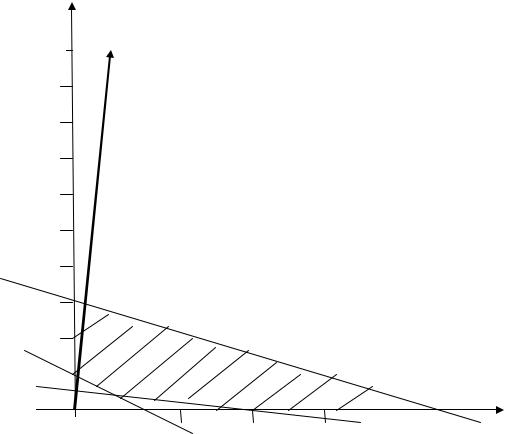
Решение. 1. На координатной плоскости OX1X2 проведем прямые линии
l1 : x1 2x2 2,	l2	: 3x1 10x2 30,	l3 :0,5x1 5x2	2,5	и по ним

построим многоугольник D - область допустимых планов (рис. 1).

Рис. 1

D есть

многоугольник M1M2M3M4M5 , где M1(0; 3) , M 2 (10; 0),

M3(5; 0),

M 4 (1,25; 0,375) , M5 (0;1).

2. Находим градиент целевой функции (рис. 1): f (1;10) .

-8 -

3.Построим семейство параллельных прямых линий, перпендикулярных вектору f (1;10) .

4. По	направлению	f	(1;10) первое касание	с многоугольником
происходит	в точке		M 4 (1,25; 0,375) (рис.	1). Следовательно

xmin (1,25; 0,375) - точка минимума.

5.Аналогично находим точку максимума: xmax (0; 3) .

6.Находим минимум и максимум целевой функции:

fmin f (1,25; 0,375) 5,

fmax f (0; 3) 30 .

Симплекс-метод. Пусть задана задача линейного программирования в

канонической форме
			f	c x max ,			Ax b , x ,
где	x (x , ..., x	n	)	-	неизвестный		n –мерный вектор, A	- матрица
	1	n
размерности m n. Не теряя общности,							можно считать, что ранг матрицы		A
равен m и m n.
	Допустимый		план		x (x , ..., x	n	) называют базисным,	если	его
					1	n
координаты можно разбить на две части:							xБ - множество базисных координат
и xН	- множество небазисных координат так, что небазисные координаты

равны нулю, а столбцы матрицы A, соответствующие базисным координатам,

линейно независимы. Базисный план называют невырожденным, если все базисные координаты положительны; иначе, называют вырожденным.

Согласно общей теории задач линейного программирования оптимальный план достаточно находить среди базисных планов. Для нахождения оптимального базисного плана, согласно симплекс-методу,

поступают следующим образом:

-9 -

1.Находят первый базисный план. Для этого систему Ax b решают методом Гаусса-Жордана, оставляя какие-то m неизвестных в одном из уравнений и исключая из остальных. Данный метод отличается от обычного метода Гаусса тем, что а) необходимо, чтобы правые части уравнений системы оставались неотрицательными;

б) неизвестное xk можно оставить в

i -ом уравнении и исключить из

j -го

уравнения, если после этого правая часть

j -го

уравнения остается

неотрицательной, т.е. выполняются условия

aik

0, bj

(a jk / aik )bi 0.

Пусть для определенности x(1) (b , ..., b

, 0, ..., 0)

- первый базисный

план. Тогда система уравнений имеет вид:

m 1

...

b ,

1,m

1,n

m,m 1

m 1

...

b .

m,n n

3. Проверим, возможно, ли текущий базисный план заменить другим

x(2) (b(2) , ..., b(2)

, 0, b(2)

, ..., b(2) , 0, ..., 0, b(2) , 0, ...,

исключая какую-то координату xi

из базиса и включая какую-то координату

xk в базис так, чтобы

f (x(1) ) f (x(2) ). Для этого номер k

выбирают из

условия

min j : j

m 1 j n

где

j c1a1 j ... cmamj , а номер i

из условия

bik

blk

: alk

1 l m

min

aik

alk

4. Если выше указанные номера k

и i

существуют, то методом Гаусса-

Жордана в последней системе неизвестное

оставляем в i -ом уравнении и

исключаем из остальных уравнений.

-10 -

5.Шаги 3, 4 повторяем до тех пор, пока возможно. После конечного числа шагов получим оптимальный базисный план.

Пример 1.2. Задачу примера 1.1. приведем к стандартной форме и решим

симплекс-методом:

f x1 10x2 0 x3 0 x4 0 x5 max,

x1 2x2 x3 2, 3x1 10x2 x4 30, 0,5x1 5x2 x5 2,5, x1 0, x2 0 .

1.Для того, чтобы найти первый базисный план, x1 исключим из второго

итретьего уравнений, x2 - из первого и второго:

x		2x	2	x			2,
	1		2	3	x4		24,
		4x2		3x3	x4		24,
		4x	2	0,5x		x	1,5,
			2	3		5

x		1,25x	0,5x	1,25,
	1	3	5	22,5,
		2,5x3 x4	x5
		x2 0,125x3	0,25x5	0,375.

Таким образом, x(1)		(1,25; 0,375; 0; 22,5; 0) - первый базисный план,

f(x(1) ) 1 1,25 10 0,375 5.

2.Систему уравнений запишем в виде

x			1,25x	0,5x	1,25,
	1	x2	3	5	0,375,
		x2	0,125x3	0,25x5	0,375,
			x4 2,5x3	x5	22,5. .
			x4 2,5x3	x5	22,5. .

3.Определим номера k и i :

3 1 ( 1,25) 10 0,125 0 2,5 0,

5 1 0,5 10 ( 0,25) 0 1 2 0,

- 11 -

1,25			22,5	1,25		i 1.
min		,			, следовательно, k 5 и
	0,5		1	0,5

4. Неизвестное x5 оставляем в первом уравнении и исключаем из

других:

x			2x	2,5x	2,5,
	5	x2	1	3	1,
			0,5x1 0,5x3
			x4 2x1	5x3	20, .

x(2) (0;1; 0; 20; 2,5) - второй базисный план,

f(x(2) ) 1 0 10 1 10 f (x(1) ) 5.

5.Повторяем предыдущие шаги до тех пор, пока возможно:

	1	0 2 10 0,5 0 ( 2) 5,
3 0 ( 2,5) 10 ( 0,5) 0 5 5 0, k 3,							i 4.
x			x	0,5x		12,5,
	5	x2	1		4	3,
		x2	0,3x1	0,1x4		3,
			x3 0,4x1	0,2x4		4, .
			x3 0,4x1	0,2x4		4, .

x(3) (0; 3; 4; 0;12,5) - третий базисный план,

f (x(3) ) 1 0 10 3 30 f (x(2) ) 10,

1 0 1 10 0,3 0 ( 0,4) 3,

4 0 0,5 10 0,1 0 0,2 1.

Таким образом, оптимальным базисным планом является

xmax (0; 3; 4; 0;12,5) ,

f (xmax ) 30.

Двойственная задача. Для задачи линейного программирования в

стандартной форме

f c x max ,

Ax b,

x ,

следующую задачу называют двойственной

1 / 61 2 3 4 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
08.06.20155.61 Mб195Мальва-24.pdf
#
08.06.20154.18 Mб79Мальва-Аксиома.pdf
#
28.03.2016333.82 Кб141математика.doc
#
08.06.2015151.55 Кб22Мельникова Анна ВКР.doc
#
08.06.201534.4 Кб69Мет.деят..docx
#
08.06.2015575.04 Кб6Метод указ по МО .pdf
#
08.06.2015303.31 Кб148Методика обучения ИЯoparina.pdf
#
08.06.201521.14 Кб130методика проведения массовых мероприятий.docx
#
08.06.201514.59 Кб36Методика Фетискина.docx
#
08.06.201519.54 Кб14Методические указания преподавателю по ЕНКМ.docx
#
08.06.201578.63 Кб187методичка внд.docx