
практическая часть
.docx
ПРАКТИЧЕСКАЯ ЧАСТЬ.
Задача 1.
Даны вершины треугольника A(-2;0), B(2;4), C(4;0).
Составить:
1) параметрические и канонические уравнения трёх сторон;
2) в общем виде уравнение медианы АЕ и высоты АD;
Решение:



B(2;4)
D




E


A(-2;0)
C(4;0)
Рис. 9 к задаче.
1)Найдём направляющий вектор стороны АВ:
АВ ={2-(-2);4-0}={4;4}, для составления параметрических уравнений стороны АВ, используем координаты точки А и вектора АВ по формуле

получаем
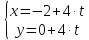 или
или
 - параметрические уравнения стороны
АВ
- параметрические уравнения стороны
АВ
Аналогично для сторон ВС и АС:
 =
=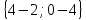 =
= ,
,
 =
= =
=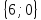
 - параметрические
уравнения стороны ВС.
- параметрические
уравнения стороны ВС.
 - параметрические
уравнения стороны АС.
- параметрические
уравнения стороны АС.
Чтобы записать уравнения сторон в каноническом виде воспользуемся
формулой:
 =
=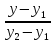 ,
для стороны АВ подставим координаты
,
для стороны АВ подставим координаты
направляющего
вектора АВ и вместо
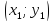 координаты точки А, получим
координаты точки А, получим
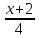 =
=
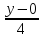 или
или
 =
=
 - канонические уравнения стороны АВ.
- канонические уравнения стороны АВ.
Аналогично для сторон ВС и АС:
 =
=
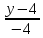 - канонические уравнения стороны ВС.
- канонические уравнения стороны ВС.
 =
=
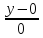 или
или
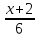 =
=
 - канонические уравнения стороны АС.
- канонические уравнения стороны АС.
2) Найдем координаты точки Е, как середину отрезка ВС
 =
= =
=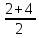 =3,
=3,
 =
= =
= =2
=> E(3;2),
по формуле
=2
=> E(3;2),
по формуле
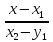 =
= ,
для точек А и Е получаем
,
для точек А и Е получаем
 =
=
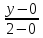 ;
;
 =5y;
2x-5y+4=0
- общее уравнение медианы АЕ.
=5y;
2x-5y+4=0
- общее уравнение медианы АЕ.
Так как высота АD
перпендикулярна стороне ВС воспользуемся
признаком перпендикулярности двух
прямых
 ·
·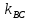 =-1.
=-1.
Перепишем
канонические уравнения стороны ВС в
общем виде, получим 2x+y-8=0, выразим отсюда
y, получим уравнение стороны ВС с угловым
коэффициентом
 в виде y=-2x+8, отсюда
в виде y=-2x+8, отсюда
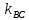 =-2,
значит
=-2,
значит
 ,
по формуле
,
по формуле
 ),
для координат точки А и
),
для координат точки А и
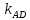 получим
получим
y-0
=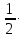 (x+1);
2y
= x+2
или x-2y+2=0
уравнение высоты АD.
(x+1);
2y
= x+2
или x-2y+2=0
уравнение высоты АD.
Иначе: нормальный вектор прямой ВС n{2;1} является направляющим
вектором высоты
АD, по формуле
 =
= для координат точки А и вектора n,
получим
для координат точки А и вектора n,
получим
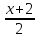 =
=
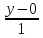 ;
x+2=2y;
x-2y+2=0
уравнение высоты АD
;
x+2=2y;
x-2y+2=0
уравнение высоты АD
Ответ: 1) AB:
 ,
,
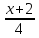 =
=
 ;
;
BC:
 ,
,
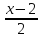 =
=
 ;
;
AC:
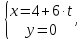
 =
=
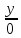 ;
;
2) AE: 2x-5y+4=0;
AD: x-2y+2=0.
Э.Ф. Капленко, С.Г. Маркова Сборник задач по геомнтрии 2 часть, стр 31
Задача 2.
Составить
уравнения прямой, проходящей через
точки
 .
.
Решение:
Найдём направляющий вектор прямой:
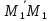 =
=
Уравнения
прямой составим по точке  и направляющему вектору
и направляющему вектору  (
(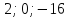 ):
):
 =
=
 ;
;
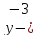 )=0
)=0
Выполним проверку:
Подставим
координаты точки
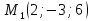 в
полученные уравнения:
в
полученные уравнения:
 =
=
 ;
;
 0
0
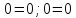
Получены верные равенства.
Подставим
координаты точки  :
:
 =
=
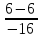 ;
;
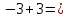 0
0

Получены верные равенства.
Вывод: канонические уравнения прямой составлены правильно.
Ответ:
 =
=

Э.Ф. Капленко, С.Г. Маркова Сборник задач по геомнтрии 2 часть, стр 36
Задача 3.
Составить
канонические уравнения прямой по точке
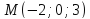 и
направляющему вектору
и
направляющему вектору

Решение:
Канонические уравнения прямой составим по формуле:

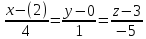
 .
.
Ответ:
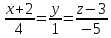 .
.
Э.Ф. Капленко, С.Г. Маркова Сборник задач по геомнтрии 2 часть, стр 45
Задача 4.
Составить параметрические уравнения следующих прямых:
а)
 =
=
 ;
;
б)
 ;
;
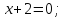
в) x=0; y-6=0.
Решение:
Прямые заданы каноническими уравнениями и на первом этапе следует найти какую-нибудь точку, принадлежащую прямой, и её направляющий вектор.
а) Из
уравнений
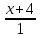 =
=
 снимаем точку и направляющий вектор:
снимаем точку и направляющий вектор:
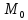 (-4;0;5),
(-4;0;5),
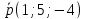 .
.
Составим параметрические уравнения данной прямой:

б)
Рассмотрим канонические уравнения
 ;
;
 .
Выбор точки здесь несложен:
.
Выбор точки здесь несложен:

Запишем
направляющий вектор
 ,
а на оставшееся место поставим
ноль:
,
а на оставшееся место поставим
ноль: 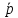 (0;7;-3)..
(0;7;-3)..
Составим
параметрические уравнения прямой:

в)
Перепишем уравнения
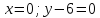 в виде
в виде

то
есть «z»
может быть любым. А если любым, то пусть,
например,  .
Таким образом, точка
.
Таким образом, точка
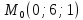 принадлежит
данной прямой. Для нахождения направляющего
вектора используем следующий формальный
приём: в исходных уравнениях
принадлежит
данной прямой. Для нахождения направляющего
вектора используем следующий формальный
приём: в исходных уравнениях
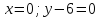 находятся
«x»
и «y»,
и в направляющем векторе на данных
местах записываем нули:
находятся
«x»
и «y»,
и в направляющем векторе на данных
местах записываем нули:
 .
На оставшееся место ставим единицу:
.
На оставшееся место ставим единицу:  .
Вместо единицы подойдёт любое число,
кроме нуля.
.
Вместо единицы подойдёт любое число,
кроме нуля.
Запишем
параметрические уравнения прямой:
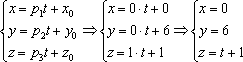
Ответ:
а)
 ;
;
б)
 ;
;
в)
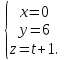
Э.Ф. Капленко, С.Г. Маркова Сборник задач по геомнтрии 2 часть, стр 44
Задача 5.
Выяснить взаимное расположение двух прямых
 :
:
 =
=
 =
= ,
,
 :
:
 =
=
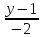 =
=
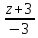 .
.

1) Вытаскиваем из уравнений точки и направляющие векторы:
 :
:
 =
=
 =
= =>
=>
 (-4;-5;6),
(-4;-5;6),
 (-2;4;6)
(-2;4;6)
 :
:
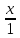 =
=
 =
=
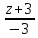 =>
=>
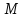 (0;1;-3),
(0;1;-3),
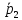 (1;-2;-3)
(1;-2;-3)
2)
Найдём вектор:
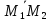 =(0-(-4);1-(-5);-3-6)=(4;6;-9)
=(0-(-4);1-(-5);-3-6)=(4;6;-9)
3) Вычислим смешанное произведение векторов:
( ·
· = -2·
= -2· -
- +4·
+4·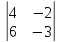 =
=
=-2·(18+18)-(-36-36)+4·(-12+12)=-72+72+0=0
Таким
образом, векторы
 компланарны, а значит, прямые
компланарны, а значит, прямые
 лежат
в одной плоскости и могут пересекаться,
быть параллельными или совпадать.
лежат
в одной плоскости и могут пересекаться,
быть параллельными или совпадать.
4)
Проверим направляющие векторы
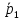 (-2;4;6),
(-2;4;6),
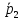 (1;-2;-3) на
коллинеарность.
(1;-2;-3) на
коллинеарность.
Составим систему из соответствующих координат данных векторов:

Из каждого уравнения
следует, что λ= -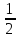 , следовательно, система совместна,
соответствующие координаты векторов
пропорциональны, и векторы коллинеарны.
, следовательно, система совместна,
соответствующие координаты векторов
пропорциональны, и векторы коллинеарны.
Вывод:
прямые  параллельны
либо совпадают.
параллельны
либо совпадают.
5)
Выясним, есть ли у прямых общие точки.
Возьмём точку
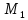 (-4;-5;6) ,
принадлежащую первой прямой, и подставим
её координаты в уравнения прямой
(-4;-5;6) ,
принадлежащую первой прямой, и подставим
её координаты в уравнения прямой 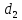 :
:
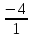 =
=
 =
=
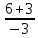 ,
,
-4≠3≠-3
Таким образом, общих точек у прямых нет, значит они параллельны.
Ответ:
 ║
║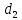 .
.
Л.С. Атанасян, В.А. Атанасян Сборник задач по геометрии часть1, стр 53
Задача 6.
Найти точку пересечения прямых
 :
:
 =
=
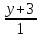 =
=
 ,
,
 :
:
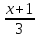 =
=
 =
=

Решение:
Перепишем уравнения прямых в параметрической форме:
 :
:
 ,
,
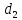 :
:

Точка
пересечения прямых M(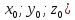 принадлежит
прямой
принадлежит
прямой  поэтому
её координаты
поэтому
её координаты
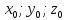 удовлетворяют
параметрическим уравнениям данной
прямой, и им соответствует вполне
конкретное значение параметра
удовлетворяют
параметрическим уравнениям данной
прямой, и им соответствует вполне
конкретное значение параметра
 :
:
M:

Но эта же точка принадлежит и второй прямой, следовательно:
M:

Приравниваем соответствующие уравнения и проводим упрощения:
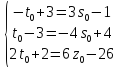 =>
=>
 =>
=>

Получена
система трёх линейных уравнений с двумя
неизвестными. Если прямые пересекаются,
то система обязательно совместна и
имеет единственное решение. Из первого
уравнения выразим
 и подставим его во второе и третье
уравнение:
и подставим его во второе и третье
уравнение:
 =>
=>
 =>
=>

Тогда:

Подставим
найденное значение параметра
 в
уравнения:
в
уравнения:
 =>
=>
 =>
=>
Для
проверки подставим найденное значение
параметра
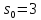 в
уравнения:
в
уравнения:
 =>
=>
 => =>
=> =>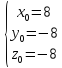
Получены те же самые координаты, что и требовалось проверить.
Ответ: M(8;-8;-8).
Л.С. Атанасян, В.А. Атанасян Сборник задач по геометрии часть1, стр 58
Задача 7.
В правильной четырёхугольной пирамиде ABCDS (с вершиной S) точка M — середина ребра SC. Постройте сечение пирамиды плоскостью ABM.
Решение.
Сечение изображено на рис. 10.

Рис. 10. К задаче
Самое главное тут — выяснить, по какой прямой секущая плоскость ABM пересекает плоскость SCD. Для этого заметим, что AB ║ CD, и по признаку параллельности прямой и плоскости имеем AB ║ SCD. А из теоремы следует тогда, что прямая MN пересечения плоскостей ABM и SCD параллельна прямой AB (и, стало быть, прямой CD).
Таким образом, MN — средняя линия треугольника SCD. Сечением пирамиды будет трапеция ABMN.
Ответ: трапеция ABMN.
Л.С. Атанасян Аналитическая геометрия часть вторая, стр 179.
Задача 8.
Докажите, что в правильной треугольной пирамиде скрещивающиеся рёбра перпендикулярны.
Решение.
Пусть ABCD — правильная треугольная пирамида (рис. 10). Докажем, например, что AD ⊥ BC.

Рис. 11. К задаче
Пусть точка M — середина ребра BC. Рассмотрим плоскость ADM. Ясно, что высота DH
нашей пирамиды лежит в этой плоскости (поскольку H лежит на медиане AM).
Докажем, что прямая BC перпендикулярна плоскости ADM. Для этого нам нужно предъявить две пересекающие прямые, лежащие в плоскости ADM и перпендикулярные BC. Какие же это прямые?
Во-первых, это прямая DH. В самом деле, будучи высотой пирамиды, DH перпендикулярна плоскости ABC. По определению это означает, что DH перпендикулярна любой прямой, лежащей в плоскости ABC - в частности, прямой BC.
Во-вторых, это прямая AM. Действительно, будучи медианой равностороннего треугольника ABC, отрезок AM является его высотой и потому перпендикулярен BC.
Итак, мы убедились, что BC ⊥ DH и BC ⊥ AM. По признаку перпендикулярности прямой
и плоскости мы заключаем, что BC ⊥ ADM. Стало быть, BC перпендикулярна любой прямой, лежащей в плоскости ADM — в частности, прямой AD. Это мы и хотели доказать.
Обратите внимание, какая схема рассуждений реализована в данной задаче. Допустим, мы
хотим доказать, что прямая l перпендикулярна прямой m. Действуем следующим образом:
1. Берём подходящую плоскость π, в которой лежит прямая l.
2. В плоскости π находим две пересекающиеся прямые a и b, такие, что m ⊥ a и m ⊥ b.
3. По признаку перпендикулярности прямой и плоскости делаем вывод, что m ⊥ π.
4. По определению перпендикулярности прямой и плоскости заключаем, что прямая m перпендикулярна любой прямой, лежащей в плоскости π. В частности, m ⊥ l, что и требовалось.
Эта схема часто работает во многих задачах.
Л.С. Атанасян Аналитическая геометрия часть вторая, стр 177
Задача 9.
Найти
точку пересечения прямой
 и плоскости
и плоскости
2x-y+z+4=0.
Решение:
Рассмотрим взаимное расположение прямой и плоскости:
3· 2 + 2· (-1) + (-1)·1 = 3 ≠ 0 , значит прямая и плоскость пересекается. Пере-
пишем уравнение прямой в параметрическом виде:

Подставим эти уравнения прямой в уравнения плоскости, найдём значение
параметра t:

Чтобы найти координаты точки пересечения прямой и плоскости подставим значение t в параметрические уравнения прямой:

Ответ:
 - точка пересечения прямой и плоскости.
- точка пересечения прямой и плоскости.
Л.С. Атанасян Аналитическая геометрия часть вторая, стр 157.
Задача 10.
Выяснить взаимное
расположение прямой, заданной точкой
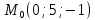 и
направляющим вектором
и
направляющим вектором
 (3;-2;4),
и плоскости 2x-3y-3z+12=0.
(3;-2;4),
и плоскости 2x-3y-3z+12=0.
Решение.
Вытащим вектор
нормали плоскости:
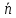 (2;-3;-3).
(2;-3;-3).
Вычислим скалярное
произведение вектора
нормали плоскости и направляющего
вектора прямой:
 ·
·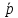 =
2·2-3·(-2)-3·4=6+66-12=0, значит, прямая либо
параллельна плоскости, либо лежит в
ней.
=
2·2-3·(-2)-3·4=6+66-12=0, значит, прямая либо
параллельна плоскости, либо лежит в
ней.
Подставим координаты
точки
 в уравнение плоскости:
в уравнение плоскости:
2·0-3·5-3·(-1)=12=0
2·0-3·5-3·(-1)+12=0
0-15+3+12=0
0=0
Получено верное
равенство, следовательно, точка 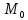 лежит в данной плоскости. Разумеется,
и любая точка прямой тоже будет
принадлежать плоскости.
лежит в данной плоскости. Разумеется,
и любая точка прямой тоже будет
принадлежать плоскости.
Ответ: прямая лежит в плоскости.
Л.С. Атанасян Аналитическая геометрия часть вторая, стр 178.
