
- •10. Уравнение прямой, заданной точкой и направляющим вектором.
- •11. Уравнение прямой, с угловым коэффициентом.
- •13. Взаимное расположение двух прямых.
- •17. Уравнение плоскости заданной точкой и двумя параллельными ей векторами.
- •18. Уравнение плоскости заданной тремя точками.
- •19. Уравнение плоскости, заданной точкой Мо и вектором нормали. Определение. Вектор, перпендикулярный плоскости, называется вектором нормали плоскости.
- •20. Взаимное расположение двух плоскостей.
- •23. Уравнение прямой, заданной как линия пересечения двух плоскостей.
- •25. Исследование формы эллипса по его уравнению
- •26. . Исследование формы гиперболы по её уравнению
23. Уравнение прямой, заданной как линия пересечения двух плоскостей.
В пространстве нельзя задать прямую точкой и вектором нормали, так как эти данные не определяют положение прямой в пространстве единственным образом. (см. Рис. 16) В тоже время, если в пространстве даны две не параллельные плоскости, то их линия пересечения ─ прямая, определённая единственным образом.
Задача
Дано: α∩β = ℓ
α: А1 х+В1 у+С1 z+D1 =0
β: А2 х+В2 у+С2 z+D2 =0.
Составить уравнение прямой ℓ
Решение

Так как точка М,
принадлежащая прямой ℓ = α ∩ β, то её
координаты одновременно удовлетворяют
как уравнению плоскости α так и уравнению
плоскости β, то есть удовлетворяет
системе уравнений

- система уравнений называется уравнением прямой, заданной как линия пересечения двух плоскостей
24. Взаимное расположение прямой и плоскости
Пусть
d
– прямая. Точка

 d
и направляющий вектор
d
и направляющий вектор
 .
Плоскость α задана уравнением:
.
Плоскость α задана уравнением: .
Возможны
следующие случаи взаимного расположения
прямой и плоскости:
.
Возможны
следующие случаи взаимного расположения
прямой и плоскости:
1) Прямая пересекает плоскость, то есть: d ∩α = N. В этом случае прямая и плоскость имеют одну общую точку.
2) Прямая параллельна плоскости, то есть: d || α. В этом случае прямая и плоскость не имеют общих точек.
3) Прямая лежит в
плоскости, то есть: d α.
В этом случае прямая и плоскость имеют
бесчисленное множество общих точек.
α.
В этом случае прямая и плоскость имеют
бесчисленное множество общих точек.
Таким образом, задача о взаимном расположении прямой и плоскости сводится к вопросу о существовании общих точек, принадлежащих как прямой, так и плоскости. Это значит, что координаты этих точек должны удовлетворять как уравнению плоскости, так и уравнениям прямой, то есть являться решением системы уравнений:

Для решения этой
системы уравнений относительно трёх
неизвестных х,у и z,
запишем её в виде:

Для решения
полученной системы четырёх уравнений
относительно четырёх уравнений, сведём
её к одному уравнению относительно
одной переменной t.
Для этого выражения для x,
y
и z
последних уравнений подставим в первое
уравнение. Таким образом получаем
уравнение для определения параметра
t,
соответствующего точки пересечения
прямой d
и плоскости :
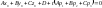
Уравнение
 имеет
единственное решение, если
имеет
единственное решение, если
Условие
 является условием пересечения прямой
и плоскости.
является условием пересечения прямой
и плоскости.
Если в уравнении
 и
и
 ,
,
то оно не имеет
решения. Таким образом, условие
 и
и является
условием параллельности прямой и
плоскости.
является
условием параллельности прямой и
плоскости.
Если в уравнении
 и
и

то оно имеет бесчисленное множество решений. Таким образом,
условие
 и
и является
условием принадлежности прямой
плоскости.
является
условием принадлежности прямой
плоскости.
25. Исследование формы эллипса по его уравнению
Пусть дан эллипс
своим каноническим уравнением (4)
 .
.
Для определения вида кривой заданной уравнением (4), заметим:
а) Координаты начала системы координат точки О(0;0) не удовлетворяют
уравнению (4). => Эллипс не проходит через начало координат.
б) Найдём точки
пересечения эллипса с осью Ох :
 =>
=> => Эллипс две точки пересечения с осью
Ох :
=> Эллипс две точки пересечения с осью
Ох : и
и
в) Найдём точки
пересечения эллипса с осью Оу :
 =>
=> => Эллипс две точки пересечения с осью
Ох :
=> Эллипс две точки пересечения с осью
Ох : и
и .
.
г) Если точка М(х;у) принадлежит эллипсу, то из уравнения (4) следует, что и точка М1(-х;у) принадлежит эллипсу. => Эллипс симметричен относительно оси Ох.
д) Если точка М(х;у) принадлежит эллипсу, то из уравнения (4) следует, что и точка М2(х;-у) принадлежит эллипсу. => Эллипс симметричен относительно оси Оу.
На основании г) и д) можно сделать вывод, что эллипс симметричен относительно начала системы координат.
е) Из уравнения
(4)
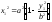 ,
, =>
=> и
и => Все точки эллипса лежат внутри
прямоугольника, ограниченного прямыми
=> Все точки эллипса лежат внутри
прямоугольника, ограниченного прямыми и
и .
.
ж) Так как
 , то можно сделать вывод, что с ростом
у от 0
, то можно сделать вывод, что с ростом
у от 0
до
 величина х убывает от
величина х убывает от до 0.
до 0.
з)
 =>
=> =>
=> =>
=>
 <0
=> Если
<0
=> Если
 ,
то
,
то ,
то есть функция
,
то есть функция выпукла вверх. Учитывая симметричность
эллипса относительно осей координат,
получаем изображение эллипса
выпукла вверх. Учитывая симметричность
эллипса относительно осей координат,
получаем изображение эллипса

Точки А1,
А2,
В1,
В2
─ называют вершинами эллипса. [A1A2]
─ большой осью эллипса, [B1B2]
─ называют малой осью эллипса. Числа
 и
и называют полуосями эллипса.
называют полуосями эллипса.
