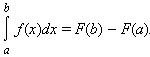Вопрос 5.

Физический смысл:  1) если задана скорость как функция от времени, то путь за время Т равен интегралу от скорости по времени;  2) если задано ускорение как функция от времени, то изменение скорости равно интегралу от ускорения по времени; Геометрический смысл: если функция y(x) больше нуля на промежутке [a;b], то площадь криволинейной трапеции, ограниченной графиком функции, осью ОХ и двумя прямыми х=а и х=b, равна интегралу от этой функции по переменной х на данном промежутке.

Вопрос 6. Основные свойства определенного интеграла

I. Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е. , где х, t – любые буквы.

II. Определенный интеграл с одинаковыми пределами интегрирования равен нулю.

III. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.

IV. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.

V. Постоянный множитель можно выносить за знак определенного интеграла.

VI. Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.

Формула Ньютона – Лейбница

Если функция f (x) интегрируема на [a; b], то для любого  существует интеграл 

который называется интегралом с переменным верхним пределом.

Если функция f интегрируема на [a; b], то функция F (x) непрерывна на этом отрезке.

Если функция f интегрируема на [a; b] и непрерывна в  то функция F (x) дифференцируема в причем 

Если функция f непрерывна на [a; b], то на этом отрезке она имеет первообразную F вида 

где C – постоянная. Всякая первообразная функции f на отрезке [a; b] удовлетворяет этой формуле.

 

Одним из основных результатов математического анализа является теорема Ньютона – Лейбница:

Пусть функция f (x) непрерывна на [a; b], а F (x) – какая-либо первообразная функции f на этом отрезке. Тогда 

Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f, вычислить ее значения в точках a и b и найти разность F (b) – F (a).

Пусть f (x) непрерывна на [a; b], g (t) имеет непрерывную производную на [α; β],  Тогда если a = g (α), b = g (β), то справедлива формула замены переменной в определенном интеграле: 

Если функции u (x) и v (x) имеют на [a; b] непрерывные производные, то справедлива формула интегрирования по частям: 

Замена переменной в определенном интеграле

ТЕОРЕМА. Пусть функция φ(t) имеет непрерывную производную на отрезке [α,β], а=φ(α), в=φ(β) и функция f(х) непрерывна в каждой точке х вида х=φ(t), где t[α,β].

Тогда справедливо следующее равенство:

Эта формула носит название формулы замены переменной в определенном интеграле.

Подобно тому, как это было в случае неопределенного интеграла, использование замены переменной позволяет упростить интеграл, приблизив его к табличному (табличным). При этом в отличие от неопределенного интеграла в данном случае нет необходимости возвращаться к исходной переменной интегрирования. Достаточно лишь найти пределы интегрирования α и β по новой переменной t как решение относительно переменной t уравнений φ(t)=а и φ(t)=в. На практике, выполняя замену переменной, часто начинают с того, что указывают выражение t=ψ(х) новой переменной через старую. В этом случае нахождение пределов интегрирования по переменной t упрощается: α=ψ(а), β=ψ(в).