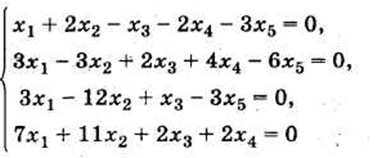Математические методы в рекламе и со

Билет 1.

1) Уравнение прямой с угловым коэффициентом

Угол наклона прямой к оси Ox в фиксированной прямоугольной декартовой системе координат Oxy на плоскости - это угол, отсчитываемый от положительного направления оси Ох до прямой против хода часовой стрелки.

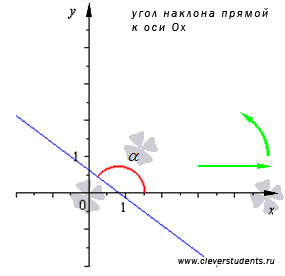
Если прямая параллельна оси абсцисс или совпадает с ней, то угол ее наклона считают равным нулю. Таким образом, угол наклона прямой  может принимать значения из интервала .

Угловым коэффициентом прямой называется тангенс угла наклона этой прямой. Угловой коэффициент прямой обычно обозначают буквой k. Тогда по определению .

Если прямая параллельна оси ординат, то угловой коэффициент не существует (в этом случае также говорят, что угловой коэффициент обращается в бесконечность).

Положительный угловой коэффициент прямой указывает на возрастание ее графика функции, отрицательный угловой коэффициент – на убывание. 

На рисунке показан угол наклона прямой и указано значение углового коэффициента при различных вариантах расположения прямой относительно прямоугольной системы координат.

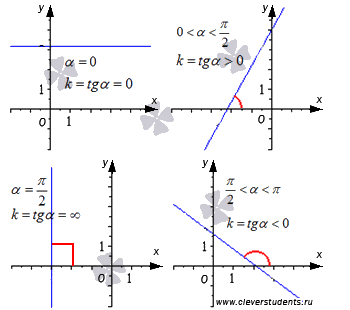
Нахождение углового коэффициента прямой при известном угле наклона к оси Ox не представляет никаких сложностей. Для этого достаточно вспомнить определение углового коэффициента и вычислить тангенс угла наклона.

Уравнение прямой с угловым коэффициентом имеет вид , где k - угловой коэффициент прямой, b – некоторое действительное число. Уравнением прямой с угловым коэффициентом можно задать любую прямую, не параллельную оси Oy (для прямой параллельно оси ординат угловой коэффициент не определен).

Давайте разберемся со смыслом фразы: «прямая на плоскости в фиксированной системе координат задана уравнением с угловым коэффициентом вида ». Это означает, что уравнению  удовлетворяют координаты любой точки прямой и не удовлетворяют координаты никаких других точкек плоскости. Таким образом, если при подстановке координат точки  в уравнение прямой с угловым коэффициентом получается верное равенство, то прямая проходит через эту точку. В противном случае точка не лежит на прямой.

2) Из 16 уток, отправившихся осенью на юг, 6 меченых. Какова вероятность того, что из 10 вернувшихся 3 меченые?

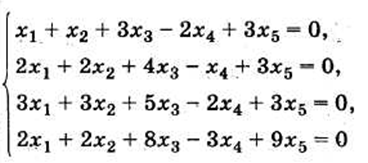
Билет 2.

1) Угол между прямыми, условия параллельности и перпендикулярности прямых

Условие параллельности

       Если прямые линии параллельны, то они наклонены к числовой оси ОХ под одним и тем же углом, следовательно, разница углов наклона параллельных прямых равна нулю (действительно они никогда не пересекаются). Тангенс угла в ноль градусов (ноль радиан) равен нулю. То есть левая часть уравнения (1-4) равна нулю, тогда нулю должна быть равна и правая часть данного выражения. Дробь равна нулю если числитель равен нулю. В нашем случае это может быть при:

k2 = k1.                                         

Это и есть условие параллельности двух прямых линий.

Условие перпендикулярности

Если две прямых линии взаимно перпендикулярны, то угол между ними равен 90 или П/2 радиан. Тангенс такого угла не существует (иногда говорят, что он равен бесконечности). Правая часть (1-4) не существует при равенстве нулю знаменателя, т.е.

k2 * k1 = -1.                                  

Условие (1-6) или что тоже самое 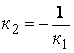является условием перпендикулярности заданных прямых.

2) В каждом из трех букетов по 10 роз. В I-ом букете 8 белых роз, во II-ом – 7 белых и в III-ем – 6 белых роз. Из каждого букета наугад выбирают по одному цветку. Найти вероятность того, что, по крайней мере, одна вынутая роза – белая.