III. Электростатика. Основные формулы

• Закон Кулона

где F - модуль силы взаимодействия двух точечных зарядов величиной q₁ и q₂, r - расстояние между зарядами,  - диэлек- трическая проницаемость среды, ₀ - диэлектрическая постоянная.

• Напряженность электрического поля

,

где - сила, действующая на точечный заряд q₀, помещенный в данную точку поля.

• Напряженность поля точечного заряда (по модулю)

,

где r - расстояние от заряда q до точки, в которой определяется напряженность.

• Напряженность поля, создаваемого системой точечных зарядов (принцип суперпозиции электрических полей)

,

где - напряженность в данной точке поля, создаваемого i-тым зарядом.

• Модуль напряженности поля, создаваемого бесконечной равномерно заряженной плоскостью:

,

где - поверхностная плотность заряда.

• Модуль напряженности поля плоского конденсатора в средней его части

.

Формула справедлива, если расстояние между пластинами много меньше линейных размеров пластин конденсатора.

• Напряженность поля, создаваемого бесконечно длинной равномерно заряженной нитью (или цилиндром) на расстоянии r от нити или оси цилиндра по модулю:

,

где - линейная плотность заряда.

• Поток вектора напряженности электрического поля:

а) через произвольную поверхность, помещенную в неоднородное поле

,

где  - угол между вектором напряженности и нормалью к элементу поверхности, dS - площадь элемента поверхности, E_n - проекция вектора напряженности на нормаль;

б) через плоскую поверхность, помещенную в однородное электрическое поле:

,

в)через замкнутую поверхность:

,

где интегрирование ведется по всей поверхности.

• Теорема Гаусса. Поток вектора напряженности через любую замкнутую поверхность S равен алгебраической сумме зарядов q₁, q₂ ... q_n, охватываемых этой поверхностью, деленной на   ₀.

.

• Вектор электрической индукции (электрическое смещение) связан с напряженностью электрического поля соотношением:

Поток вектора электрического смещения выражается аналогично потоку вектора напряженности электрического поля:

а) поток сквозь плоскую поверхность, если поле однородно

б) в случае неоднородного поля и произвольной поверхности

,

где D_n - проекция вектора на направление нормали к элементу поверхности, площадь которой равна dS.

• Теорема Гаусса. Поток вектора электрической индукции сквозь замкнутую поверхность S, охватывающую заряды q₁, q₂ ... q_n , равен

,

где n - число зарядов, заключенных внутри замкнутой поверхности (заряды со своим знаком).

• .Потенциал электрического поля  = , где q_о - точечный положительный заряд, помещенный в данную точку поля, W - потенциальная энергия заряда q в данной точке поля.

• Потенциальная энергия системы двух точечных зарядов Q и q при условии, что W_ = 0, находится по формуле:

W = ,

где r - расстояние между зарядами. Потенциальная энергия положительна при взаимодействии одноименных зарядов и отрицательна при взаимодействии разноименных.

• Потенциал электрического поля, созданного точечным зарядом Q на расстоянии r

 = ,

• Потенциал электрического поля, созданного металлической сферой радиуса R, несущей заряд Q:

 = (r ≤ R; поле внутри и на поверхности сферы),

 = (r > R; поле вне сферы).

• Потенциал электрического поля, созданного системой n точечных зарядов в соответствии с принципом суперпозиции электрических полей равен алгебраической сумме потенциалов ₁, ₂,…, _n, создаваемых зарядами q₁, q₂,..., q_n в данной точке поля

 =.

• Связь потенциалов с напряженностью:

а) в общем случае = -qrad или = ;

б) в случае однородного поля

Е = ,

где d - расстояние между эквипотенциальными поверхностями с потенциалами ₁ и ₂ вдоль силовой линии;

в) в случае поля, обладающего центральной или осевой симметрией

где производная берется вдоль силовой линии.

• Работа, совершаемая силами поля по перемещению заряда q из точки 1 в точку 2

A = q(₁ - ₂),

где (₁ - ₂) - разность потенциалов начальной и конечной точек поля.

• Разность потенциалов и напряженность электрического поля связаны соотношениями

(₁ - ₂) = ,

где Е_е - проекция вектора напряженности на направление перемещения dl.

• Электроемкость уединенного проводника определяется отношением заряда q на проводнике к потенциалу проводника .

.

• Электроемкость конденсатора :

,

где (₁ - ₂) = U - разность потенциалов (напряжение) между обкладками конденсатора; q - модуль заряда на одной обкладке конденсатора.

• Электроемкость проводящего шара (сферы) в СИ

с = 4₀R,

где R - радиус шара,  - относительная диэлектрическая проницаемость среды; ₀ = 8,8510^-12 Ф/м.

• Электроемкость плоского конденсатора в системе СИ:

,

где S - площадь одной пластины; d - расстояние между обкладками.

• Электроемкость сферического конденсатора (две концентри- ческие сферы радиусами R₁ и R₂, пространство между которыми заполнено диэлектриком , с диэлектрической проницаемость  ):

.

• Электроемкость цилиндрического конденсатора (два коакси-альных цилиндра длиной l и радиусами R₁ и R₂ , пространство между которыми заполнено диэлектриком с диэлектрической проницаемостью  )

.

• Емкость батареи из n конденсаторов, соединенных после- довательно, определяется соотношением

.

• Емкость батареи из n конденсаторов, соединенных парал- лельно: с =.

Последние две формулы применимы для определения емкости многослойных конденсаторов. Расположение слоев параллельно пластинам соответствует последовательному соединению однослойных конденсаторов; если же границы слоев перпендикулярны пластинам, то, считают, что имеется параллельное соединение однослойных конденсаторов.

• Потенциальная энергия системы неподвижных точечных зарядов

.

Здесь _i - потенциал поля, создаваемого в той точке, где находится заряд q_i, всеми зарядами, кроме i-го; n - общее число зарядов.

• Энергия заряженного конденсатора меняется в результате каких-либо процессов, ее целесообразно вычислять через те из величин q и u, которая в данном процессе не изменяется. Так, если заряд конденсатора не изменился, то W = 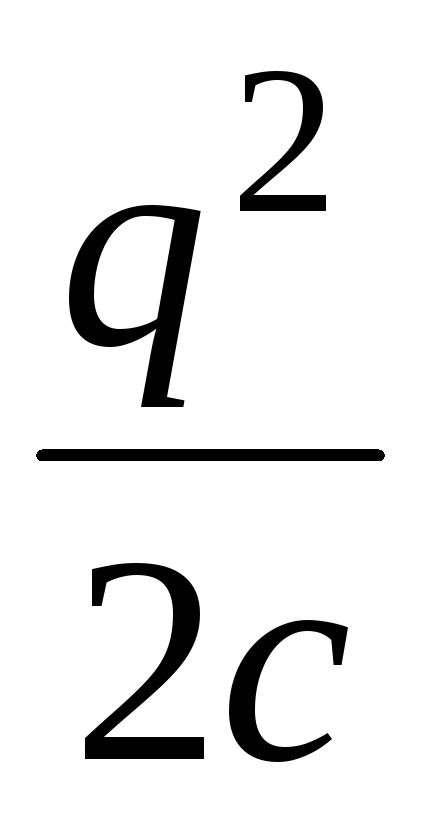, если напряженность не изменяется, то W = независимо от того, как меняется при этом емкость конденсатора.

• Объемная плотность энергии электрического поля (энергия, отнесенная к единице объема):

 = ==,

где D - величина вектора электрического смещения.

• Энергия однородного поля:

W = V.

• Энергия неоднородного поля:

W =.