
Физика / Физика 1 часть / Метод.ч.1 стр.74-83
.doc

Рис.9
![]() .
(3)
.
(3)
Напряженность
поля в точке нахождения заряда q
равна
![]()
Так как векторы
![]() и
и
![]() взаимно перпендикулярны, то
взаимно перпендикулярны, то
![]() .
.
Подставляя выражения (2) и (3) в это равенство, получим
 .
(4)
.
(4)
Подставив выражение (4) в формулу (1), получим
![]() .
(5)
.
(5)
Убедимся, в том, что правая часть равенства (5) дает единицу силы
![]()
![]() = Н.
= Н.
Произведем
вычисления по формуле (5), учитывая, что
![]()
![]()
Направление
силы
![]() ,
действующей на положительный заряд q,
сов- падает с направлением вектора
напряженности
,
действующей на положительный заряд q,
сов- падает с направлением вектора
напряженности
![]() .
Из рис. 9 следует, что
.
Из рис. 9 следует, что
![]() ,
откуда
,
откуда
![]() .
.
Произведем вычисления подставив численные значения величин:
![]() .
.
Пример 4.
Два точечных
электрических заряда q1
= 1 нКл и
q2
= -2
нКл находятся
в воздухе на расстоянии
d
= 10
см друг от
друга. Определить напряженность
![]() и потенциал
поля, создаваемого этими зарядами в
точке А,
удаленной от заряда q1
на расстояние
r1
= 9
см и от заряда
q2
на r2
= 7
см.
и потенциал
поля, создаваемого этими зарядами в
точке А,
удаленной от заряда q1
на расстояние
r1
= 9
см и от заряда
q2
на r2
= 7
см.
|
Дано:
q1 = 1·10-9 Кл q2 = -2·10-9 Кл d = 0,1 м r1 = 0,09 м r2 = 0,07 м |
Решение:
Согласно
принципу суперпозиции электрических
полей, каждый заряд создает поле
независимо от присутствия в пространстве
других зарядов. Поэтому напряженность
|
|
|
даваемых каждым зарядом в отдельности:
![]() .
.
Напряженности
электрического поля, создаваемого
в воздухе (
= 1) зарядами
q1
и
q2
равны:
![]() ,
(1)
,
(1)
![]() .
(2)
.
(2)
Вектор
![]() (рис. 10) направлен по силовой линии от
заряда q1,
так как этот заряд положителен; вектор
(рис. 10) направлен по силовой линии от
заряда q1,
так как этот заряд положителен; вектор
![]() направлен также по силовой линии, но к
заряду
q2,
так как этот заряд отрицателен.
направлен также по силовой линии, но к
заряду
q2,
так как этот заряд отрицателен.
Модуль вектора
![]() найдем по теореме косинусов
найдем по теореме косинусов
![]() ,
(3)
,
(3)
где
- угол между
векторами
![]() и
и
![]() ,
который может быть найден
,
который может быть найден
из треугольника со сторонами r1, r2 и d:
![]() .
.
В данном случае во избежание громоздких записей удобно значение cos вычислить отдельно:
![]() .
.
r2
r1 d α
А
○![]()
![]()







|
q1 q2 |
Подставляя
выражение
|
Рис. 10 В соответствии с принципом су-
перпозиции электрических полей потенциал результирующего поля, создаваемого двумя зарядами q1 и q2, равен алгебраической сумме потенциалов:
![]() (4)
(4)
Потенциал электрического поля, создаваемого в вакууме точечным зарядом q на расстоянии r от него, выражается формулой:
![]() .
(5)
.
(5)
В нашем случае согласно формулам (4) и (5) получим
![]() или
или
![]() (6)
(6)
Произведем
вычисления учитывая, что
![]()

![]()
![]()
Пример 5
Чему равна напряженность электрического поля равномерно заряженного стержня с линейной плотностью в точке, находящейся на расстоянии R от оси стержня? Углы, образованные стержнем и прямыми, проходящими через его концы и точку A равны, соответственно 1 и - 2 .
|
Дано: R 1 - 2 |
Решение: Расстояние от исследуемой точки поля A до оси стержня может быть любым, поэтому заряд на стержне не является точечным. Выделим на стержне элемент длины dl (рис.11). На нем располагается элементарный заряд dq = dl, который можно считать точечным. |
|
E - ? |
Напряженность поля, созданного зарядом dq в исследуемой точке, можно разложить на две составляющие, одна из которых перпендикулярна, а другая - параллельна оси стержня.
![]() (1)
(1)
Обозначим
угол между радиусом - вектором
![]() и стержнем.
Радиус- вектор направлен от элемента
dl
к точке А.
Тогда
и стержнем.
Радиус- вектор направлен от элемента
dl
к точке А.
Тогда
dE= dEsin , dE|| = dE cos (2)
|
Рис.
11 |
Прежде чем интегрировать вы- ражения (2), нужно преобразо- вать выра жение (1) так, чтобы можно было интегрировать по углу. Выразим элемент дли- ны проводника dl через d. Из рис. 11 видно что
но
|
Подставив dl и r в формулу (1), получим
![]() (3)
(3)
Ч
(7)
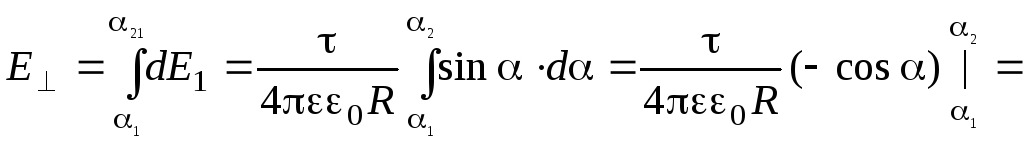
(6)![]()

![]() .
(5)
.
(5)
Модуль
вектора
![]() равен:
равен:
![]() .
.
Чтобы избежать громоздких записей, преобразуем сначала подкоренное выражение:
(cos1
-
cos2)2
+
(sin2
- sin1)2
=
cos21
+ cos22
– 2cos1
cos2
+ + sin22
+ sin21
– 2sin2sin1
= (sin21
+ cos21)
+ (sin22
+ cos22)
– – 2(sin1
sin2
+ cos1
cos2)
= 2[1 – cos(1
- 2)]
=
![]() .
.
Тогда модуль напряженности:
 (6)
(6)
Чтобы найти
направление вектора
![]() ,
определим угол :
,
определим угол :

Рассмотрим частный случай: точка А находится против середины стержня. Тогда из соображений симметрии E|| = 0, E = E и cos2 = - cos1. С учетом этого формула (4) примет вид:
![]() .
(7)
.
(7)
При
этом 1
=
- 2.
Покажем, что в предельных случаях поле,
образованное заряженной нитью конечной
длины, переходит в электрическом
поле
бесконечно протяженной нити и точечного
заряда. Из чертежа видно,
что
cos1
= cos(
- 2)
=
![]() ,
где L
- длина стержня.
,
где L
- длина стержня.
а)
При R<<L
величиной R
можно пренебречь и cos1
1. Отсюда
![]() - это
напряженность поля бесконечной
протяженной нити. Подставим значение
cos1
в формулу напряженности (7)
- это
напряженность поля бесконечной
протяженной нити. Подставим значение
cos1
в формулу напряженности (7)
![]()
![]()
Произведение L = q, т.е. заряду, находящемуся на нити.
б)
При R>>L
величиной
L/2
можно пренебречь, тогда
![]() и
и
![]() - это напряженность поля точечного
заряда.
- это напряженность поля точечного
заряда.
Пример 6.
В вакууме образовалось скопление зарядов в виде тонкого длинного цилиндра с объемной плотностью =1·10-10 Кл/м3 и радиусом R =10 см. Найти напряженность поля в точках, отстоящих от оси цилиндра на расстоянии 5 см и 15 см, а также вид зависимости Е(r).
|
Дано:
R = 0,1 м = 1·10-10 Кл/м3 r1 = 0,05 м r2 = 0,15 м = 1 |
Решение:
Через точки 1 и 2 проведем в виде цилиндров радиусом r1 и r2 замкнутые поверхности (рис.12). Поток вектора напряженности, пронизывающий боковую поверхность цилиндра радиуса r1, равен: NE(1) = E12r1 l, где l - длина образующей цилиндра. (Поток через основание цилиндра равен нулю).
|
|
|
Е1 = ? Е2 = ? Е(r) = ? |
||
|
l ●2
Рис. 12
|
По теореме Гаусса:
.Отсюда: E12r1l
=
Точка
1 находится внутри цилиндра радиуса
R.
Поэтому
для любой точки с
|
|
E(r)
=
![]() ,
,
т.е. напряженность линейно растет с увеличением расстояния.
![]() Поток
напряженности, пронизывающий поверхность
второго цилиндра, находится аналогично
Поток
напряженности, пронизывающий поверхность
второго цилиндра, находится аналогично
По теореме Гаусса
NE(2)
=![]() =
=
![]() .
.
Приравнивая правые части равенств, найдем
E2
=
![]() .
.
Зависимость Е(r) при r > R имеет вид
E(r)
=
![]()
Напряженность
убывает пропорционально![]() .
При r
=
R
.
При r
=
R
ER
=
![]() =
=
![]()
На поверхности цилиндра напряженность имеет максимальную величину.
Проверим единицы напряженности
[E]
=
![]() =
=![]() =
=![]() .
.
Произведем
вычисления учитывая, что
![]()
![]()
E2
=
![]()
Графически зависимость Е(r) представлена на (рис.13).
-
r
0
R
2R
3R
4R
5R
6=R
7R
E
0
ER
ER/2
ER/3
ER/4
ER/5
ER/6
ER/7

E
ER
0 R 2R 3R 4R 5R 6R 7R r
Рис. 13
Пример 7.
Тонкая квадратная рамка равномерно заряжена с линейной плотностью заряда =100 нКл/м. Определить потенциал поля в точке пересечения диагоналей (рис. 14).
|
Дано:
=1·10-10 Кл/м |
Решение:
Заряд, находящийся на рамке, нельзя считать точечным, он равномерно распределен по длине квадратной рамки. Поэтому для нахождения потенциала используем принцип суперпозиции |
|
φА - ? |
полей. Согласно ему, потенциал поля квадратной рамки равен алгебраической сумме потенциалов полей, создаваемых
зарядом каждой стороны квадрата. Из соображений симметрии следует, что эти потенциалы равны по величине и одинаковы по знаку: 1 = 2 = 3 = 4. Тогда = 4i.
Выделим на рамке малый участок dl с зарядом dQ = ·dl. Этот заряд можно рассматривать как точеч-
|
dr r где r - расстояние от элемента dl до точки 0. Для интегри- рования нужно преобразовать эту формулу так, чтобы в ней была только одна переменная - угол . Согласно чертежу
Тогда |
A B
α1 dα dl
α2 K O
D C Рис. 14 |
d
=
![]() =
=![]() .
.
Точка K делит сторону квадрата AD пополам. Тогда AD = 2AK. При
в ычислении
потенциала φАК
интегрирование ведется от α1=π/4
до α2=π/2.
ычислении
потенциала φАК
интегрирование ведется от α1=π/4
до α2=π/2.

П![]() роверим
единицы потенциала
роверим
единицы потенциала








 .
.












