
Лабораторная работа №14
Численное решение задачи Коши для обыкновенного дифференциального уравнения первого порядка
Цели лабораторного занятия:
Численное решение задачи Коши методами Эйлера и Рунге – Кутта.
Задачи лабораторного занятия:
1.Реализация алгоритмов Эйлера и Рунге – Кутта.
2.Экспериментальная проверка влияния шага на погрешность решения задачи.
3.Оформление отчета по выполненной работе.
Содержание |
|
Лабораторная работа №14. Численное решение задачи Коши для обыкновенного |
|
дифференциального уравнения первого порядка........................................................................................ |
2 |
Численное решение задачи Коши............................................................................................................ |
2 |
Задание 1................................................................................................................................................... |
3 |
Методические рекомендации.................................................................................................................... |
3 |
Задание 2................................................................................................................................................... |
4 |
Задание 3................................................................................................................................................... |
4 |
Задание 4................................................................................................................................................... |
5 |
Задания для самоподготовки.................................................................................................................... |
5 |
Контрольные вопросы............................................................................................................................... |
5 |
Лабораторная работа №14. Численное решение задачи Коши для обыкновенного дифференциального уравнения первого порядка
Лабораторная работа №14. Численное решение задачи Коши для обыкновенного дифференциального уравнения первого порядка
Численное решение задачи Коши
Численное интегрирование задачи Коши для обыкновенных дифференциальных уравнений предполагает нахождение решения дифференциального уравнения
dy/dx = f(x, y) |
(1) |
на отрезке |
|
[x= x0; x= xmax]. |
(2) |
Решение дифференциального уравнения удовлетворяет начальному условию |
|
y(x0 ) = y0. |
(3) |
Функция f(x, y) может быть задана или в аналитической форме, или в виде таблицы. |
|
Погрешность найденного решения не должна превышать ε. |
|
Наиболее простым методом решения задачи является метод Эйлера, алгоритм которого задается следующим выражением:
yi+1 = yi + h f(xi ; yi ), i = 0, 1, 2, …N-1, |
(4) |
где h – шаг интегрирования, который принят постоянным на всем интервале интегрирования,
N – число участков разбиения интервала интегрирования. Погрешность этого метода пропорциональна h.
Существенно меньшую погрешность вычислений обеспечивает метод Рунге – Кутта четвертого порядка, алгоритм которого задается следующими расчетными формулами:
yi+1 = yi + (h/6)(K1 + 2K2 + 2K3 + K4 ); K1 = f(xi ; yi );
K2 = f(xi + h/2; yi + h K1 /2);
K3 = f(xi + h/2; yi + h K2 /2); (5) K4 = f(xi + h; yi + h K3);
i = 0, 1, 2, …N-1,
где N – число участков разбиения интервала интегрирования.
Погрешность метода Рунге – Кутта четвертого порядка пропорциональна h4, так что этот метод заметно точнее предыдущего.
2
Лабораторная работа №14. Численное решение задачи Коши для обыкновенного дифференциального уравнения первого порядка
Оба рассмотренных метода относятся к одной группе – методам Рунге – Кутта. Метод Эйлера – это метод Рунге – Кутта первого порядка.
Погрешности решения задачи Коши на каждом шаге интегрирования методами Рунге – Кутта можно оценить по формулам (6), (7):
= |y2i. h/2 – yi. H |; |
(6) |
δ = / | ymax |, |
(7) |
где y2i, h/2 и yi, h – это значения решения задачи при одном и том же значении аргумента, но найдены они численным методом при различных значениях шага интегрирования вычислительного процесса – h/2 и h соответственно;
–оценка абсолютной погрешности решения;
δ– оценка относительной погрешности решения; ymax – наибольшее значение решения с шагом h/2.
В случае, если найденное решение удовлетворяет требованиям к погрешности искомого ответа, можно прекратить итерационный процесс. В противном случае необходимо повторить вычисления с меньшим шагом (например, в 2 раза) и вновь выполнить проверку.
Задание 1
Найти решение методической задачи (7) методами Эйлера и Рунге – Кутта четвертого
порядка. Погрешность δ решения не должна превышать 1% на всем интервале интегрирования. Построить графики решений: аналитического, по методу Эйлера, по методу Рунге – Кутта.
dy/dx = -2y+1, y(0) = 0, 0 |
≤ x ≤ 3. |
(8) |
Аналитическое решение задачи Коши (8) – экспоненциальная зависимость (9): |
|
|
y(x) = (1 – e-2x) / 2. |
|
(9) |
Методические рекомендации
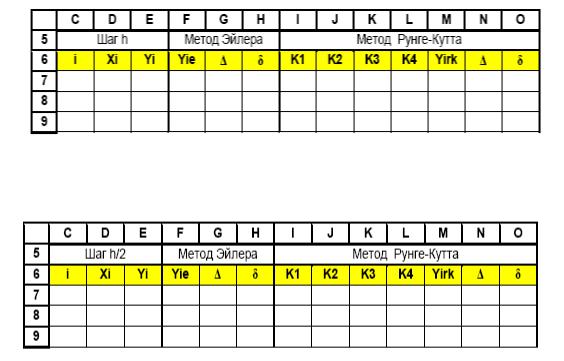
Результаты вычислений рекомендуется свести в таблицы. Возможный вариант показан на примере таблиц 1, 2. В одной из таблиц получены решения двумя методами для шага h, в другой – для шага h/2.
Уменьшать значение шага следует до тех пор, пока не будет обеспечено заданное значение погрешности d.
Аналитическое решение (в таблицах обозначено Yi) используется для расчета погрешностей численного решения задачи. Абсолютные погрешности решений вычисляются по соотношениям:
● для метода Эйлера
= |yi – yie|, |
(10) |
3
Лабораторная работа №14. Численное решение задачи Коши для обыкновенного дифференциального уравнения первого порядка
● для метода Рунге – Кутта
= |yi – yirk|. |
(11) |
Относительные погрешности |
|
δ = /ymax(x), |
(12) |
при этом ymax(x)=1/2.
Таблицы и графики можно разместить на одном или на разных рабочих листах. Вариант размещения таблиц на различных листах представляется более удобным.
Таблица 1
Результаты вычислений для значения шага h
Таблица 2
Результаты вычислений для значения шага h/2
Задание 2
Найти максимальные значения погрешностей для каждого из расчетов, выполненных по конкретному алгоритму с заданным значением шага.
Построить таблицы и графики зависимостей максимальных значений погрешности от числа участков разбиения интервала интегрирования N для методов Эйлера и Рунге – Кутта.
Провести анализ полученных данных, сформулировать выводы.
Задание 3
Найти решение задачи Коши для своего варианта задания методами Эйлера и Рунге –
Кутта четвертого порядка. Погрешность δ решения не должна превышать 1% на всем интервале интегрирования. Оценки погрешностей провести по формулам (10)-(12). Построить графики решений.
4
Лабораторная работа №14. Численное решение задачи Коши для обыкновенного дифференциального уравнения первого порядка
Задание 4
Оформить отчет по выполненной работе.
Задания для самоподготовки
1.Повторить теоретический материал.
2.Дать геометрическую интерпретацию решения задачи Коши методом Эйлера.
3.Разработать форму вычислительного бланка и подготовить необходимые данные для выполнения задания в табличном процессоре.
4.Построить блок-схемы алгоритмов решения задачи Коши для обыкновенного дифференциального уравнения методами Эйлера и Рунге – Кутта четвертого порядка.
Контрольные вопросы
1.Как формулируется задача Коши для обыкновенного дифференциального уравнения?
2.Почему возникает необходимость в численных методах решения задачи Коши?
3.Укажите принципиальные различия численного и аналитического решения задачи Коши.
4.Запишите расчетные соотношения для метода Эйлера и метода Рунге – Кутта четвертого порядка?
5.Как оценивают погрешность решения задачи Коши численным методом?
6.Почему рассмотренные методы решения задачи Коши называют итерационными?
7.Как влияет выбор шага на погрешность решения задачи Коши?
8.Какой критерий следует использовать для завершения итерационного процесса?
5
