2. Исследование точности слежения астатических систем на примере радиолокационных станций (рлс)

2.1. Вывод формулы передаточной функции замкнутой системы для ошибки по задающему воздействию

На рис. 10 изображена W(p) – передаточная функция разомкнутой системы, которая по определению равна , гдеY(p) - изображение выходной (регулируемой) величины y(t), E(p) изображение ошибки (рассогласования). Кроме того, здесь обозначена g(t) входная (задающая) функция.

Рис. 10. Структурная схема замкнутой системы.

H(p) – передаточная функция замкнутой системы, которая получается из разомкнутой замыканием отрицательной обратной связью.

В этом случае (17).

С другой стороны, по определению передаточная функция замкнутой системы равна отношению изображения выходной величины к изображению входной , гдеG(p) изображение задающей функции (входной величины).

Ошибка системы e(t)=g(t) – y(t). Переходя к изображениям, E(p)=G(p) – Y(p).

Тогда передаточная функция замкнутой системы для ошибки по задающему воздействию

(18)

Установившуюся ошибку системы e_уст определим как , которая в соответствии с теоремой о конечном значении

При вычислении установившейся ошибки передаточную функцию для ошибки H_e(p) раскладывают в степенной ряд по степеням р в окрестности точки р=0:

, (19)

где ; k=0,1,2… коэффициенты ошибок.

Для изображения установившейся ошибки из исходного выражения (2) получим:

.

Переходя во временную область, найдем

; .

При анализе РЛС слежения за подвижной целью в качестве входного воздействия принимается полиномиальная функция

,

где - начальное значение задающего воздействия,- начальная скорость и- начальное ускорение, с которыми изменяется задающее воздействие.

Принятая модель входного воздействия охватывает все возможные виды движения цели: при 0 и ==0 имеем дело с зависшим вертолетом, при0 и =0 - равномерно летящий самолет, при0 - маневрирующий самолет, выполняющий боевой разворот с целью выхода из зоны захвата РЛС. Более подробно принятая модель иллюстрируется рис. 11. С учетом введенной функции входного воздействия установившаяся ошибка системы будет:

где ;k=0,1,2… - составляющая установившейся ошибки системы по k-й производной.

Если функция g(t) имеет конечное число m отличных от нуля производных, т.е. когда g(t) – полиномиальная функция, то полученный выше бесконечный ряд превращается в полином, содержащий (m+1) слагаемых.

Из последнего равенства следует, что при полиномиальном задающем воздействии основная составляющая установившейся ошибки определяется коэффициентом ошибки с наименьшим индексом, т.е. коэффициентом с₀, если он отличен от нуля, коэффициентом с₁ при с₀=0, коэффициентом с₂ при с₀=с₁=0, и т.д.

2.2. Математическое описание системы рлс и анализ точности слежения

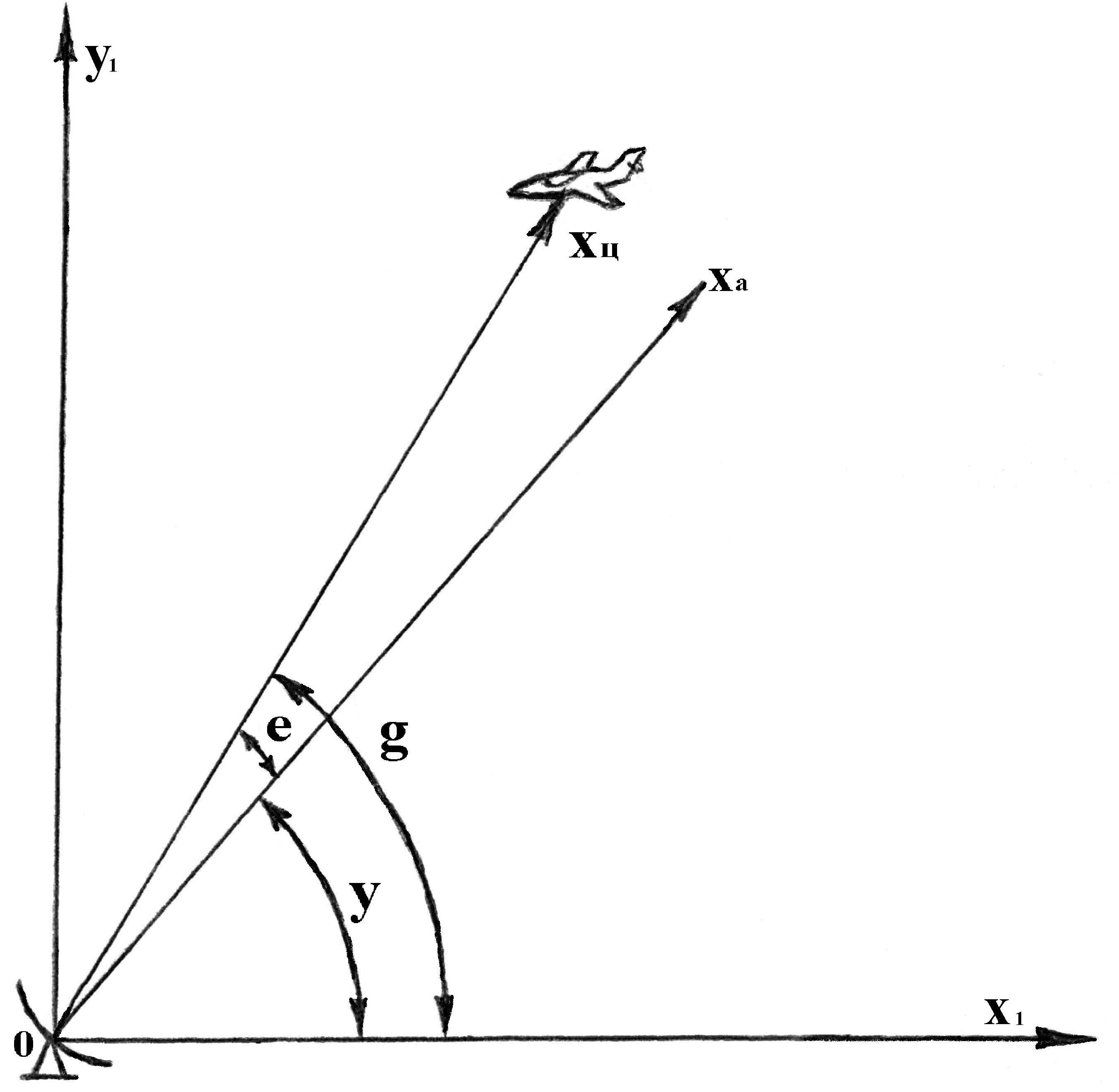
На рис. 11 показана схема слежения РЛС за подвижной целью, при этом на рисунке изображена геометрическая интерпретация основных параметров замкнутой следящей системы РЛС. Выходной (регулируемой) величиной здесь является y(t) – угловое положение оси симметрии излучающей антенны (х_а) относительно исходной инерциальной системы координат x₁0y₁. Из рис. 12 видно, что эта ось х_а определяет положение равносигнальной зоны. Ось 0х_ц направлена на подвижную цель, и ее положение определяет входное (задающее) воздействие g(t). Разница углов между осью симметрии антенны и направлением на цель является рассогласованием (ошибкой) следящей системы РЛС: e(t)=g(t) – y(t). Основное требование, предъявляемое к следящей системе, это равенство нулю ошибки слежения, т.е. направление оси симметрии антенны точно на цель вне зависимости от ее маневров. На рис. 13 показана статическая характеристика дискриминатора, т.е. датчика угла рассогласования, формирующего ошибку слежения РЛС в зависимости от положения цели относительно излучающих зон радиолокатора. При отклонении цели на величину, большую ширины радиолуча (>e_M) происходит потеря цели.

Реальная система РЛС содержит большое количество звеньев, являющихся датчиками угла рассогласования, усилителями, корректирующими звеньями, исполнительными органами, объектом управления, которые описываются передаточными функциями первого или второго порядка, но лишь некоторые из них играют решающую роль в определении предельной ошибки рассогласования. Поэтому при дальнейшем изложении будем учитывать лишь эти звенья.

Пусть эквивалентная передаточная функция системы соответствует инерционному звену с передаточной функцией статического звена . Признаком статического звена является наличие слагаемого 1 в знаменателе передаточной функции.

Рис. 13. Статическая характеристика дискриминатора.

В этом случае передаточная функция для ошибки замкнутой системы по входному воздействию будет иметь вид

.

В этом случае, коэффициент ошибок по «0» производной, т.е. по углу рассогласования, будет (3)

.

Можно показать, что для статической системы (т.е. для системы c астатизмом нулевого порядка) все коэффициенты ошибок отличны от нуля. При этом основную роль играет уже полученный коэффициент ошибки , так как при полиномиальном задающем воздействииg(t) этот коэффициент определяет наиболее быстро нарастающую во времени составляющую установившейся ошибки. На рис. 14 показана величина установившейся ошибки при слежении за неподвижной целью (зависший вертолет).

Рис. 14. Установившаяся ошибка Рис. 15. Установившаяся ошибка

статической системы. астатической системы.

Рассмотрим астатическую систему с астатизмом первого порядка. В этом случае система содержит одно интегрирующее звено, а ее эквивалентная передаточная функция не содержит в качестве обязательного слагаемого 1 в знаменателе. Пусть передаточная функция разомкнутого контура содержит одно интегрирующее звено . В этом случае коэффициент передачиk₁ имеет размерность , и является добротностью следящей системы по угловой скорости, т.е. предельным установившимся значением угловой скорости системы.

Передаточная функция замкнутой системы для ошибки по входному воздействию

;

Коэффициент ошибки по координате .

Коэффициент ошибки по угловой скорости .

Таким образом, для системы с астатизмом первого порядка установившейся ошибки по углу нет (рис. 15), а величина установившейся ошибки по угловой скорости обратно пропорциональна добротности следящей системы по скорости.

Система с астатизмом второго порядка содержит два интегрирующих звена . В этом случае равны нулю первые два коэффициента ошибок С₀=С₁=0 и основным коэффициентом ошибки является коэффициент .

Вообще, для астатической системы с астатизмом r-го порядка обращаются в нуль первые r коэффициентов ошибок, т.е. С₀=С₁=…= С_r-1=0 и первым отличным от нуля является r-й коэффициент ошибки .

Итак, при полиномиальном воздействии установившаяся ошибка приближенно может быть определена как - для статической системы,- для системы с астатизмом первого порядка,- для системы с астатизмом второго порядка,- для системы с астатизмомr-го порядка.

Вообще-то следует отметить, что реально астатические системы с астатизмом выше второго порядка не применяются, так как при этом возникают большие сложности с обеспечением их устойчивости.

Таким образом, для статической системы установившаяся ошибка зависит от постоянной составляющей входного воздействия, для астатической системы первого порядка – от скорости изменения входного воздействия и не зависит от постоянной составляющей входного сигнала. Для астатической системы второго порядка установившаяся ошибка зависит от ускорения входного воздействия и не зависит от постоянной составляющей входного воздействия и скорости его изменения.

Если входное воздействие постоянно по величине, то астатическая система с астатизмом любого порядка имеет нулевую ошибку, а при постоянной скорости изменения входного воздействия астатическая система второго порядка имеет нулевую ошибку.

Принятая полиномиальная модель входного воздействия определяет закон равноускоренного движения цели и охватывает все возможные виды движения от равномерного движения до боевого разворота с максимально возможным ускорением, при котором цель пытается выйти из зоны обнаружения РЛС.

Можно отметить еще одно важное свойство астатических систем: они обладают памятью по входному воздействию. Так, астатическая система второго порядка обладает памятью по скорости входного воздействия, и если вдруг пройдет помеха по цепям управления и дискриминатор кратковременно отключится, то система будет продолжать следить за подвижным объектом «по памяти», отрабатывая скорость движения объекта. Тем самым значительно повышается помехозащищенность астатических систем. Астатическая система второго порядка измеряет не только угловые координаты движущегося объекта (цели), но и скорость его движения.

Указанные замечательные свойства астатических систем имеют весьма прозрачное физическое объяснение процесса управления: введение в контур управления интегрирующих звеньев означает интегрирование (суммирование) накопленной суммарной ошибки и введение через отрицательную обратную связь противодействия этой ошибке.