1.2. Частотные характеристики

Частотные характеристики системы математически получаются из передаточной функции при подстановке p=j. Физически они получаются при подаче на вход системы гармонического (синусоидального) сигнала постоянной амплитуды и разной частоты и измерении амплитуды и фазы выходного сигнала.

Пусть входной сигнал ; выходной сигнал; беря отношение выходного сигнала к входному, получим частотную передаточную функцию или комплексный коэффициент передачи:

(7)

Здесь использованы 2 формы записи: тригонометрическая и алгебраическая. Амплитудно-частотная характеристика (АЧХ) определяет фильтрующие свойства системы, а фазовая частотная характеристика (ФЧХ) () определяет запаздывание выходного сигнала по отношению к входному. P() – вещественная частотная характеристика, Q() – мнимая частотная характеристика.

Рассмотрим эти характеристики на примере апериодического звена, представляющего RC-цепочку (элементарный фильтр низкой частоты (ФНЧ)) (рис.1).

Рис. 1. ФНЧ.

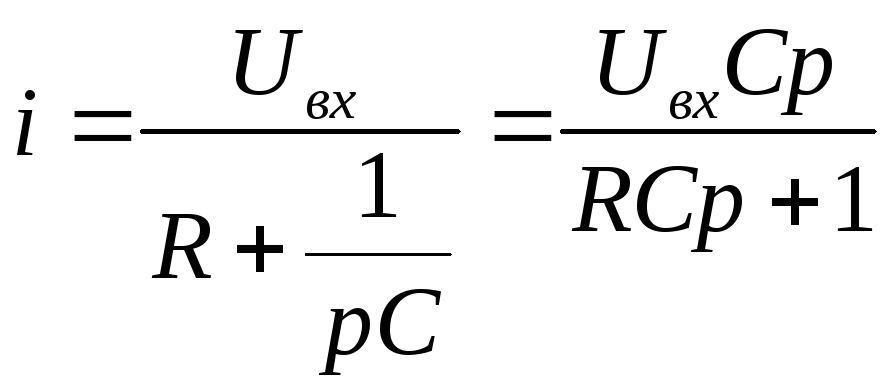Выведем передаточную функцию для этого звена. Комплексное сопротивление емкости , гдеp=j. Ток в контуре ; выходное напряжение.

,

где T=RC – постоянная времени цепочки с размерностью [RC]=c. Коэффициент передачи такой цепочки k=1. Передаточная функция содержит один полюс . Для нахождения частотных характеристик примемp=j, . Для перевода мнимой единицы в числитель умножим числитель и знаменатель на комплексно-сопряженное выражение

(8)

(9)

(10)

Вычислим значения амплитуды и фазы в нескольких характерных точках А(0)=1; А()=0; ;(0)=0; ;.

На рис. 2,3 построены АЧХ и ФЧХ ( - полоса пропускания фильтра).

Рис. 2. АЧХ ФНЧ. Рис. 3. ФЧХ ФНЧ.

На комплексной плоскости P, jQ построим АФЧХ (рис. 4) по ранее вычисленным значениям амплитуды и фазы.

Рис. 4. АФЧХ ФНЧ.

Рассмотрим также частотные характеристики еще для одной элементарной RC-цепочки (элементарный фильтр высокой частоты (ФВЧ)) (рис. 5).

Передаточная функция цепочки

, (11)

Рис. 5. ФВЧ.

где T=RC – постоянная времени инерционной дифференцирующей цепочки.

Передаточная функция содержит один нуль (q₁=0) и один полюс .

Подставляя p=j, получим

(12)

(13)

(14)

Рис. 6. АЧХ ФВЧ. Рис. 7. ФЧХ ФВЧ.

Рис. 8. АФЧХ ФВЧ.

1.3. Логарифмические амплитудные характеристики (лах) системы

При анализе систем автоматического регулирования большое распространение получил метод логарифмических частотных характеристик (ЛАХ). Для решения многих задач (исследование устойчивости системы, качества процесса регулирования и пр.) он позволяет значительно сократить объем вычислительных процедур и тем самым уменьшить трудоемкость исследований. Рассмотрим методику построения ЛАХ на примере апериодического звена с передаточной функцией ; АЧХ для этого звена . ЛАХ для него, где амплитудное значениеL() вычисляется в децибелах (дБ). Прологарифмируем заданное выражение

(15)

Напомним, какова связь между децибелами и обычными единицами. Если коэффициент передачи звена (коэффициент усиления) k=10, то в дБ это будет 20lg10=20дБ, при k=100 20lg100=40дБ; k=1 20lg1=0дБ; k=0,1 20lg0,1= 20дБ; k=0,01 20lg0,01= 40дБ. Итак, мы выяснили, что по оси ординат шкала равномерная. По оси абсцисс (частот) принимается логарифмическая шкала, причем интервалы частоты берутся подекадно, причем на одну декаду отводится один и тот же отрезок оси, а сама декада соответствует десятикратному изменению частот.

Вводится понятие частоты сопряжения , которая равна частоте среза или модулю нулей и полюсов передаточной функции.

И последнее, номиналы декад выбираются так, чтобы они охватывали весь диапазон частот сопряжения.

С учетом сказанного, ЛАХ запишем в виде:

(16)

При частоте меньшей частоты сопряжения (<_C) второе слагаемое под корнем представляет правильную дробь, а в квадрате ее величина гораздо меньше 1 и этой величиной пренебрегают. То есть, до частоты сопряжения ЛАХ представляет из себя прямую, параллельную оси частот: L()=20lgk.

При >_C ,намного больше 1, и пренебрегают 1 под корнем:, при=10_С имеем ; т.е. после частоты сопряжения ЛАХ представляет собой прямую линию с наклоном.

Пусть в нашем примере численные значения параметров следующие: k=5; T=0,05 с; 20lgk=200,7=14 дБ, .

Рис. 9. ЛАХ.

Для удобства построения ЛАХ следует на выбранной координатной сетке провести шаблоны с наклоном и(пунктир на рис. 9).