ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ РФ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«САМАРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Кафедра «Электронные системы и информационная безопасность»

Техническая кибернетика Лабораторный практикум Самара

Самарский государственный технический университет

2009

УДК 681.32

Техническая кибернетика: лабораторный практикум / Сост. И.В. Тихомиров, В.В. Сбродов. – Самара; Самар. гос. техн. ун-т, 2009. - 36 с.: ил.

Исследуются передаточные функции и частотные характеристики различных звеньев аналоговых систем управления. Исследуется точность слежения астатических систем на примере радиолокационных станций.

Предназначен для студентов специальностей 090104, 170105, 220203 и других родственных специальностей.

УДК 681.32

Рецензент: Зав. кафедрой «Радиотехнические устройства»

ИТФ СамГТУ

доцент, к.т.н. В.П. Свиридов

© И.В. Тихомиров, В.В. Сбродов, 2009

© Самарский государственный

технический университет, 2009

Содержание

Цель работы	4
Теоретический курс	4
1. Основные сведения	4
1.1. Передаточные функции и дифференциальные уравнения системы	4
1.2. Частотные характеристики	6
1.3. Логарифмические амплитудные характеристики (ЛАХ) системы	10
2. Исследование точности слежения астатических систем на примере радиолокационных станций (РЛС)	12
2.1. Вывод формулы передаточной функции замкнутой системы для ошибки по задающему воздействию	12
2.2. Математическое описание систем РЛС и анализ точности слежения	15
Описание лабораторных работ	20
Перечень исходных данных	20
Лабораторная работа № 1. Исследование и вывод дифференциальных уравнений и передаточных функций фильтра	22
Лабораторная работа № 2. Исследование логарифмических амплитудных характеристик (ЛАХ) фильтра	24
Лабораторная работа № 3. Исследование амплитудно-частотных (АЧХ), фазо-частотных (ФЧХ) и амплитудно-фазовых частотных (АФЧХ) характеристик фильтра	27
Лабораторная работа № 4. Построение переходной характеристики, АФЧХ, ЛАХ для заданной системы с помощью пакета прикладных программ «CLASSIC»	30
Требования к отчету	33
Контрольные вопросы	33
Библиографический список	34
Приложение. Инструкция по работе с программой «CLASSIC»	35

Цель работы

Целью работы является изучение методик расчета основных характеристик различных звеньев, входящих в любую систему автоматического регулирования, и проведение аналитического и численного (на ПЭВМ) их исследования.

теоретический курс

1. Основные сведения

1.1. Передаточные функции и дифференциальные уравнения

системы

Передаточной функцией звена или системы W(p) (в форме преобразования Лапласа) называется отношение изображения выходной величины Х_вых(р) к изображению входной величины Х_вх(р) при нулевых начальных условиях:

(1)

Функция времени х_вых(t) преобразуется в функцию Х_вых(р) комплексного аргумента p=j при помощи прямого преобразования Лапласа

(2)

В общем виде передаточная функция любой системы представляет собой отношение двух полиномов

(3)

Пусть q₁, q₂ …q_m – корни уравнения Q(p)=0 (нули передаточной функции); р₁, р₂, …р_n – корни уравнения P(p)=0 (полюса передаточной функции).

Тогда передаточную функцию системы можно записать через соответствующие корни уравнений числителя и знаменателя в виде элементарных сомножителей

(4)

Вынесем q_i и p_j за скобки и обозначим ,.

В зависимости от вида корней (действительные или комплексно-сопряженные) выражение для передаточной функции можно представить состоящим из следующих элементарных звеньев

(5)

Это будут звенья с передаточным функциями:

1. Усилительное звено W(p)=k.

2. Инерционное (апериодическое) звено .

3. Интегрирующее звено .

4. Чисто дифференцирующее звено W(p)=kp.

5. Колебательное звено .

6. Дифференцирующие (форсирующие) звенья первого и второго порядка W(p)=(1+Tp), W(p)=1+2Tp+T²p².

7. Звено чистого запаздывания .

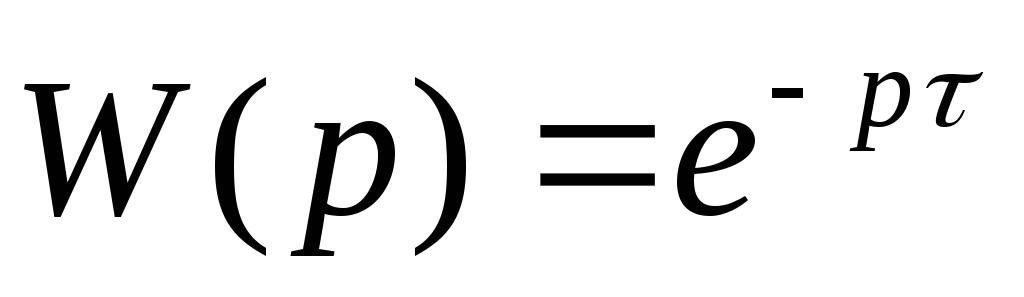Полагая р равным оператору дифференцирования из передаточной функции звена сразу получаем дифференциальное уравнение. Например, для апериодического звена

; ;

Раскрывая пропорцию и полагая , получим линейное неоднородное дифференциальное уравнение первого порядка

; (6)