3.3. Направление мощности, переносимой высшими гармониками у эп – источника гармоник.

В предыдущем примере (рис. 3.3) рассмотрим направление мощности, потребляемой двигателем постоянного тока. Эта мощность состоит из двух слагаемых:

а) Мощность, обусловленная постоянными слагающими тока и напряжения

Ро = Io * Uo.

В любой момент времени Io > 0, Uo >0, следовательно, всегда Po >0, т.е. мощность, переносимая постоянным током направлена от источника питания к ЭП.

Рис.3.4. Мощность гармоники.

б) Мгновенная мощность р_Г, обусловленная переменными слагающими тока и напряжения р_Г = i_Г * u_Г пульсирует во времени (рис.3.4). Она равна нулю в моменты перехода тока и напряжения через нуль. В остальное время она отрицательна, т.к. знаки i_Г * u_Г противоположны. Это означает, что мощность, переносимая гармоникой, направлена от ЭП к источнику питания.

Таким образом, полная мощность ЭП: Р = Ро – Рг.

Пример. Проверка баланса мощности.

Рис.3.3.а. Расчет мощности переменной составляющей тока.

Мощность , отдаваемая источником: Рист = 0,5*(12*3 + 12*1) = 24 Вт.

Мощность, получаемая ЭП: Рэп = 0,5*(6*3 + 10*1) = 14 Вт.

Пользуясь методом наложения:

Мощность, получаемая ЭП на постоянном токе РэпПост = 2*8 = 16 Вт.

Мощность, получаемая ЭП на переменном токе РэпПост = -2*1 = -2 Вт.

Из 16 Вт, полученных на постоянном токе, ЭП превращает 14 Вт в полезную работу и возвращает 2 Вт назад в виде мощности гармоники.

Потери при передаче постоянной составляющей: ΔРпост = 2² * 2 = 8 Вт.

Потери при передаче назад переменной составляющей: ΔРпер = 1² * 2 = 2 Вт.

Общие потери: ΔР = 8 + 2 = 24 – 14 = 10 Вт.

3.4. Разложение периодических функций в ряд, метод наложения.

Разложение в ряд Фурье позволяет применить классические методы расчета и анализа электрических цепей с синусоидальными токами и напряжениями для цепей с несинусоидальными токами и напряжениями.

Любая периодическая функция f(ωt) может быть представлена суммой постоянной составляющей и синусоид разных частот kω, где k – целые числа, начиная с единицы.

, где

Со – постоянная составляющая,

n – число учитываемых гармоник,

A_km- амплитуда гармоники k,

Ψ – начальная фаза гармоники k.

Первая гармоника ряда называется основной, а остальные – высшими гармониками (ВГ).

Для расчета цепи с несинусоидальными напряжениями и токами используют метод наложения, который содержит три этапа:

а) Несинусоидальное напряжение раскладывается в ряд Фурье

u = f(t) = u₀ + u₁ + u₂ + …+ u_k + …+u_n .

б) Для всех напряжений находят токи в функции времени i₀, i₁, i₂,…i_k,…i_n.

в) Мгновенные значения токов суммируются.

Рассмотрим пример расчета тока конденсатора, к которому приложено несинусоидальное напряжение, состоящее из первой и третьей гармоник, причем амплитуда третьей гармоники втрое меньше амплитуды первой (рис 3.5).

. Сопротивление конденсатора на третьей гармонике в три раза меньше сопротивления на первой гармонике , поэтому амплитуда тока 3-й гармоники равна амплитуде тока 1-й гармоники:

.

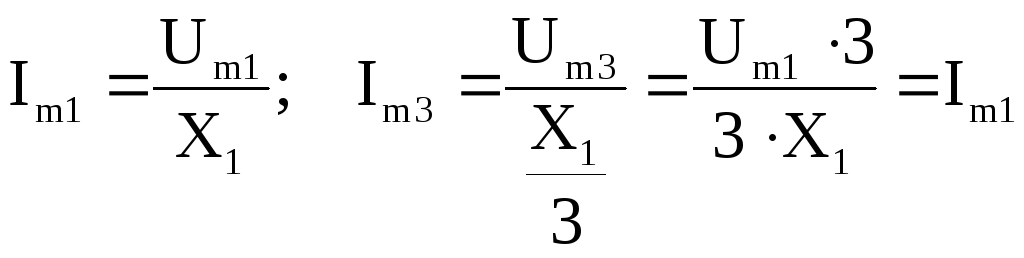Рис.3.5. Построение кривой тока в цепи с конденсатором методом наложения.

В итоге содержание тока 3-й гармоники в кривой тока втрое превышает содержание 3-й гармоники в кривой напряжения, кривая тока более несинусоидальна, чем кривая напряжения.

В цепях с реактивными сопротивлениями (индуктивным или емкостным), величина которых зависит от частоты (X_L=L, X_C= 1/С) отличается от формы кривой напряжения. В цепи с емкостью высшие гармоники усиливаются, а в цепи с индуктивностью – подавляются.