Глава III испарение и конденсация

СУЩНОСТЬ ПРОЦЕССОВ ИСПАРЕНИЯ И КОНДЕНСАЦИИ

Испарение —процесс перехода вещества из жидкого или твердого состояния в парообразное (газообразное). Испарение твердых тел — процесс непосредственного перехода при нагревании твердого тела в парообразное, минуя жидкое состояние, называют возгонкой или субли­мацией.

Испарение лежит в основе многих процессов нефтегазопереработки при разделении веществ (например, ректификация, перегонка,нагрев сы­рья втрубчатых печах,регенерация растворителей), регазификации сжи­женных газов,сушке.

Испарение может происходить с поверхности жидкости и в ее объеме, последнее на­зывают кипением.Процесс испарения интенсифицируется с повышением температуры и по­нижением давления. Для отрыва молекул от жидкой фазы и перехода их в паровую или газо­вую необходимо затратить энергию, называемуюскрытой теплотой испарения.Теплота ис­парения по своей величине равна теплотеконденсациии зависит от температуры и давления процесса, уменьшаясь с приближением их ккритическим величинам.При испарении в адиа­батических условиях тепло отбирается от испаряющейся жидкости, вследствие чего происхо­дит ее охлаждение. Испарение в закрытой емкости происходит до тех пор, пока насыщен­ные пары вещества не заполнят пространство над жидкостью.

Конденсация— процесс перехода вещества из парообразного состоя­ния в жидкое; осуществляется путем охлаждения или сжатия и охлаждения пара при температурах ниже критических для данного вещества, при этом процесс сопровождается выделением теплоты конденсации. При конденса­ции резко уменьшается объем среды и образуется вакуум. Это обстоятель­ство обусловило использование конденсаторов для создания вакуума. Кон­денсация применяется для: получения в жидком виде продуктов, выводи­мых из аппаратов в парообразном состоянии; сжижения природных, по­путных газов, паров хладагентов в холодильных установках и т.п.

Процесс частичного испарения жидкости или конденсации паров, проводимый для получения одного из продуктов обогащенного НКК или высококипящим ВКК, называется перегонкой.Образующийсяпри этом отгон в паровой фазе, обогащенный НКК, подвергают в дальнейшем кон­денсации.

Испарение жидкости или конденсацию паров осуществляют различ­ными способами: однократным, многократным и постепенным.

Однократное испарение (ОН) и однократная конденсация (ОК). Эти

процессы характеризуются тем, что образовавшиеся паровая и жидкая фазы не разделяются до окончания процесса, а при достижении конечной температуры их разделяют в один прием, однократно. При этом прини­мают, что образовавшиеся паровая и жидкая фазы находятся в состоянии равновесия. Примером процесса ОН является частичное испарение жид­кого сырья, поступающего в ректификационную колонну из трубчатой печи.

Многократное испарение и многократная конденсация. Эти процессы состоят в неоднократном повторении процессов ОН или ОК для более полного разделения исходной смеси. Так, многократное испарение состоит из повторяющегося процесса однократного испарения. Образовавшиеся

Рис. ИМ. Схемы основных видов процессов испарения и конденсации:

а — в —испарение: а — однократное (ОИ);6 —многократное (двукратное);в —

постепенное; г — е— конденсация:z— однократная (ОК);д— многократная (двукратная)¹, е — постепенная.1, V —испарители;2, 2\ 5, 5’ —сепараторы;3, 3'— конденсаторы;4 — приемники

при испарении пары отделяют в несколько ступеней. Причем во второй ступени осуществляется ОИ жидкой фазы, образовавшейся в первой ступени, а в третьей ступени — ОИ жидкой фазы, поступающей из второй ступени разделения, и т.д. Соответственно при многократной конденса­ции на последующую ступень разделения поступают пары, оставшиеся после отделения от них конденсата на предшествующей ступени разделения.

Постепенное испарение и постепенная конденсация. Эти процессы осуществляются так, что пары, образовавшиеся при испарении (или жид­кость при конденсации), удаляются из системы непрерывно в момент их образования. Образовавшиеся в системе паровая и жидкая фазы всегда на­ходятся в состоянии равновесия. Процессы постепенного испарения и кон­денсации можно рассматривать как предельный случай многократного про­цесса при бесконечно большом числе ступеней разделения. Примером про­цесса постепенного испарения является перегонка из куба периодического действия.

В промышленных установках процессы испарения и конденсации проводятся при изобарных или близких к ним условиях.

На рис. Ill-1 приведены схемы основных видов процессов испарения и конденсации.

ОДНОКРАТНОЕ ИСПАРЕНИЕ (КОНДЕНСАЦИЯ)

Бинарные смеси. Рассмотрим материальный и тепловой балансы процесса ОИ двухкомпонентной смеси.

Материальный баланс процесса однократного испарения может быть представлен уравнениями: общий

F=G+ д;

для низкокипящего компонента Fx_f = Gy+ дх.

Совместное решение приведенных уравнений дает выражение x_F= еу + (l-ejx,

где отношение массы образовавшихся паров Gк массе исходной смесиF называетсямассовой долей отгонаи обозначается через е.

Аналогично может быть составлено уравнение материального баланса ОИ в мольных единицах:

Хр = е'у'+ (l-е'^х'. (III. 1)

Отношение GкFестьмольная доля отгона,обозначаемая через е'. Поскольку образовавшийся пар и жидкий остаток находятся в равновесии, т.е.

У' = К_ах\

уравнение (III. 1) можно представить в виде

Заменив хсогласно уравнению (11.29), получим

X'f [Ка -K_w- 1 — К,

е' =

K_a-l^l-K_w^

Из уравнения (III.2) можно определить мольную долю отгонаепри заданной мольной концентрации НКК в исходной смесиx_Fи известных температуреtи давлениипв сепараторе.

Для взаимного пересчета массовой еи мольнойе’долей отгона проведем следующие преобразования. Число молей образовавшихся при ОИ паров равноFe/M_ytгдеМ_у —средняя мольная масса паров. Это же число молей будет равноFeVM_CM,гдеМ_см —мольная масса исходной жидкой смеси. Отсюда получим соотношение

еМ_см - с'М_у. (Ш.З)

Обычно М_см>М_у,поэтому е' > е.

Возможны случаи, когда значения давлений насыщенных паров компонентов существенно различаются, т. е. Р_а » P_wилиК_а » K_w .В этих условиях ВКК можно считать практически нелетучим (например, отгонка растворителя от масла) и для расчета доли отгона е' можно использовать более простое соотношение

Процесс ОИ связан с подводом тепла Q_a.Без учета теплопотерь тепло, которое содержится в паровой и жидкой фазах, образовавшихся в результате процесса ОИ, должно быть равно теплу исходной жидкостиO_f и теплуQ_Btподведенному со стороны для осуществления процесса испарения:

О _F+Qв ~Fh_tp + О_в — GH_t+gh_t .

Имея в виду, что д= F- G,

⁽ о_н '

К* у

V ^г У

получим

ч-

-Л/

Введем понятие о приведенной энтальпии сырья 0, которая определяет количество введенного тепла, приходящегося на единицу массы исходного сырья

0 = h_t +

*F

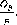
Тогда можно записать

Gв - л,x_F-х е = — = — = —

(III .4)

^F H_t -h_t У-*

На энтальпийной диаграмме уравнение (III.4) представляет собой уравнение прямой, проходящей через три точки (рис.III-2):c(x_fl0),w(x, h_t) иd(y,Н,).

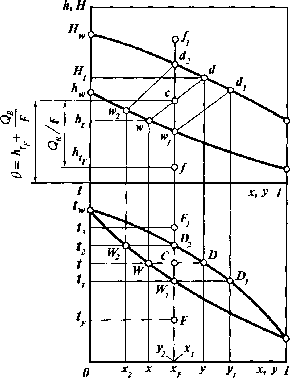
Процесс однократного испарения (однократной конденсации) можно проанализировать при помощи изобарных температурных кривых и энтальпийной диаграммы.

Исходной жидкой смеси, поступающей на ОИ при температуре t_Fи концентрации НККx_Ftотвечает точкаFна графике изобар и точка / на энтальпийной диаграмме. На обеих диаграммах нагревание исходной жид­кой смеси от температурыt_Fдо температурыt,соответствует перемеще­нию по вертикали: на графике изобар от точкиFдо точкиW_itа на эн­тальпийной диаграмме от точки / доw_t,при этом состав исходной смеси не меняется. В точкеW_t(илиWj) температура смесиt_f(или энтальпия) со­ответствует температуре ее кипения при е = 0.

Образующийся при этом пар у_;находится в равновесии с исходной жидкостью.

Для осуществления нагрева сырья от температуры t_Fдоtему сообща­ется теплоО_в(точки С и с). Положение точки с определяется ординатой 0 и абсциссойx_F,а точки С — ординатойtи абсциссойx_F.

В точке С (или с) система будет состоять из жидкой и паровой фаз составов хи у. Составы и энтальпии жидкости и пара, образовавшихся в процессе ОИ, определяются точкамиW(илиw) и D(илиd).

Уравнение (III.4) соответствует прямой wd.Сопоставив это уравнение с отрезками прямых на рис. Ш-2, получим соотношение:

Рис. Ш-2. Процесс ОИ (ОК) бинарной смеси на изобарных температурных кривых и энтальпийной диаграмме

н

а

WC wc е = —,

WD wd

т.е. отрезок WC(илиwc)пропорционален массе отгонаG.Соответственно отрезокCD(илиcd)пропорционален массе жидкого остатка. Длина конодыWD(илиwd)пропорциональна массе исходной жидкой смесиF.

При нагреве смеси до температуры t₂она полностью перейдет в паро­образное состояние (е = 1). Состав образовавшегося парау₂соответствует точкеD₂(илиd₂),при этому₂=x_F.Состав и энтальпия последней порции жидкости определяются точкамиW₂иw₂.

Величина х₂показывает, что четкого разделения компонентов путем ОИ достичь не удается, так как в конце испарения в жидкости еще содер­жится значительное количество НКК;t₂есть температура конца однократного испарения.

При температуре системы t₂ > t₂(точкиF, иf_}), более высокой, чем температура конца однократного испарения, система будет состоять из перегретых паров составаx_F.

При понижении температуры системы от t₃доt_Fбудет происходить охлаждение паров, а начиная с точки £>₂(илиd₂) — их конденсация.

Степень конденсации гпаровой фазы при температуреtопределится следующим образом:

₁ д F -G CD cd

Г =1-е = — = = = .

F F WD wd

При понижении температуры паров длина отрезка CD(илиcd)увели­чивается, что соответствует повышению степени конденсации.

Многокомпонентные смеси. При разделении многокомпонентных и сложных смесей, характерных для нефтегазопереработки и нефтехимии, любой компонент путем однократного испарения будет распределяться в определенном соотношении между отгоном и остатком.

Материальный баланс процесса однократного испарения для любого (z-го) компонента многокомпонентной смеси запишется в виде

*Ь=е'У\+(l-e')x;. (III.5)

Образовавшаяся паровая фаза состава у/ будет находиться в равно­весии с жидким остатком состава х/, т. е.

у/ = к, х; .

С учетом этого, уравнение (III.5) можно представить в виде x'_F = е'К, х'+ (l- е')х'.

Следовательно, покомпонентный состав жидкого остатка будет определяться выражением

(Ш.6)

Поскольку

I*; =i.

/=1

то из уравнения (III.6) получим

i,F

1 + е'\ К; - 1

л

= 1.

(III.7)

у

Уравнение (III.7) связывает долю отгонае,температуру и давление системы. В этом уравнении температура системы присутствует в косвенном виде, оказывая влияние через посредство давления насыщенных паров (констант фазового равновесия) компонентов, являющегося функцией температуры.

При заданных составе исходной смеси x‘_iF,давлениики температуреtуравнение (III .7) используется для определения методом последовательных приближений доли отгона е'. С этой целью задают значение доли отгонае\определяют по уравнению (III.6) концентрации компонентов в жидкой фазе и затем проверяют выполнение уравнения (III.7). Если полу­ченная сумма равна единице, то значение доли отгона е' выбрано правильно. В противном случае необходимо задать новую величинуе\добиваясь, чтобы сумма, стоящая в левой части уравнения (III.7), стала равной единице с желаемой степенью точности.

При полном ОИ исходной смеси е' = 1, тогда из уравнения (III.7)

получим

т.е. приходим, к уравнению изотермы паровой фазы.

Из уравнения (IIL8) можно определить температуру начала конден­сации паров при заданном давлениик.

Уравнение (III.7) дает большую точность при больших долях отгона. При малых долях отгона используют другое уравнение.

Выразив х/через у/ согласно уравнению равновесия, и подставив полученное в уравнение (III.5), получим

Kf = ^е'^к,у; +(l-e')-—

' К]

или

l + e'lKj - 1

Поскольку

±у;=i-

то

= 1. (III.9)

Это уравнение и используется для расчетов при малых долях отгона ё. Из уравнения (III.9) методом последовательных приближений можно найти температуру кипения смеси прие= 0:

п

1=1

Это и есть уравнение изотермы жидкой фазы.

Мольные массы паровой и жидкой фаз, образующихся в процессе ОИ, определяют по уравнениям: для паровой фазы

= X М, у';

;=1

для жидкой фазы м,=£ м,

/=1

Массовую долю отгона находят по уравнению (III.3).

Массовые концентрации любого компонента в равновесной паровой и жидкой фазах определяют из соотношений

Приведенные выше уравнения для расчета однократного испарения многокомпонент­ной смеси могут быть использованы и для расчета однократной конденсации многокомпо­нентной смеси, так как составы фаз и их относительные количества зависят только от ко­нечных температуры и давления, а не от того, каким путем данная система получена: нагре­вом и однократным испарением жидкости или охлаждением и однократной конденсацией паров.

При однократной конденсации многокомпонентной смеси е‘(илие) определяет мольную (или массовую) долю несконденсировавшихся паров, а 1 —е —г' (или 1 — е = г) — мольную (или массовую) долю образовавшегося конденсата.

Уравнения (III.7) и (Ш.9) могут быть использованы также для определения температуры смеси при заданных давлении и доле отгона или давления при заданных температуре и доле отгона.

Сложные смеси. При расчете ОН (или ОК) нефти и нефтепродуктов, содержащих весьма большое число компонентов (так называемые сложные смеси), исходный продукт разбивают на ряд фракций, кипящих в узких температурных пределах. Свойства каждой узкой фракции отождествляют со свойствами индивидуального компонента, температура кипения которо­го равна средней температуре кипения данной узкой фракции. За концент­рацию принимают относительное содержание рассматриваемой узкой фракции в смеси. Определение доли отгона, состава фаз и температуры системы производят по уравнениям, приведенным выше для многокомпо­нентной смеси.

Более точные результаты могут быть получены при представлении нефтяных смесей, состоящих из бесконечно большого числа компонентов и характеризуемых непрерывными (интегральные и дифференциальные) кривыми распределения составов.

На рис. Ш-З приведены типичные кривые распределения составов сложной смеси.

Кривые распределения отражают зависимость состава смеси от коэф­фициента относительной летучести а, который соответствует определен­ной температуре кипения компонента t.При изображении кривых распре-

б

а

и

Х(а)

Х(а)

Рис. Ш-З. Кривые распределения составов сложной смеси: а — интегральная; 6 — дифференциальная

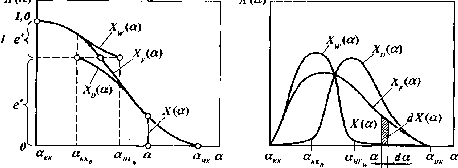
деления составов малыми концентрациями ВКК в отгоне и НКК в остатке можно пренебречь и определять составы в пределах изменения относитель­ной летучести от а_кк^ до а_нк, и от а_ккдо а_нк^ соответственно для отгона и остатка.

Наибольшую величину коэффициента относительной летучести (а_нк)

имеет НКК, наименьшую (а_кк)— ВКК. На интегральной кривойх'(а)дано суммарное содержание всех компонентов, коэффициенты относительной летучести которых имеют пределы от а доа_нк.Одна из форм уравнения для представления таких кривых имеет вид

(ШЛО)

		( \ 1 а 1д	2
х((а) = ехр	-а
		^ ®кк у

где а —постоянный коэффициент для данной смеси.

Дифференциальная кривая распределения Х'(а) дает зависимость

*,(<*)

тангенса угла наклона интегральной кривой от а, т.е.

dx'(a)

da

Если продифференцировать уравнение (ШЛО) по переменной а,то по­лучим

ig-

a

X' (a) = - = 0,8686a —exp

da

a

	(. а '	2~
-а	ig—
	1 aKK J

Очевидно, что

a

x'(a)=j*X'(a)da.

«НК

Материальный баланс процесса ОИ сложной смеси можно записать следующим образом:

x'_F (a) = e'x'_D (a) + (l - e')x^ (a)

или в дифференциальной форме

X'_F(a)da=e'X'_D(a)da+ (l-e')x^,(a)da. (III. 11)

Поскольку пары отгона и жидкий остаток находятся в равновесии, то можно записать, что

X'_D (a) = tf(a)x^ . (III. 12)

Из уравнений (III. 11) и (ШЛ2) получим:

Из уравнения (III. 15) методом последовательных приближений можно определить долю отгона епри заданных температуре и давлении системы, а затем по уравнениям (III. 14) и (III* 12) рассчитать кривые распределения остатка и отгона (см. рис. Ш-З).

При е= 1 получаем уравнение изотермы паровой фазы сложной смеси

1 + e'fff(a) - ll

Проинтегрировав выражение (III. 13) в пределах от до а**, получим

<*кк

(111*16)

X’_F (a)da = (l + e'[x(a - l)|x^ (a)da, откуда

, _x X'_F (ajda

Xw «^^a = г¹/, ,

^v ' 1 + еШ-1

(III. 13)

ИЛИ

X^(a) =

X'_F (a)

(III. 14)

I

«НК

X'_F |ajda 1 + е'[к(а) - l]

-1.

(III. 15)

Из выражения (III. 16) методом последовательных приближений может быть найдена температура начала конденсации сложной смеси.

При малых долях отгона для расчета е' можно использовать аналогичное выражение, полученное из уравнения (III. 11) в случае замены

Х^(а) на согласно уравнению равновесия.

Из уравнения (III. 11) получим

Хо (a)d

a =

K(ajXp (ajda 1 + e |к(а) - l|

(III.17)

или

tf(ajx^ (a)

1 + е'[к(а) - lj

(111*18)

Проинтегрировав выражение (III. 17) в пределах отa_HKдоa_KK, полу­чим

^акк

J

“нк

к[ар(р (ajda 1 + e'|/((aj - lj

= 1.

Долю отгона е' сложной смеси находят методом последовательных приближений по уравнению (III. 18).

При е= 0 получим уравнение изотермы жидкой фазы для сложной смеси

«кк

Jк(aJX_F(ajda= 1.

^aHK

Из этого выражения методом последовательных приближений можно определить температуру начала кипения сложной смеси.

При расчете однократного испарения (конденсации) многокомпонент­ных и сложных смесей углеводородов в присутствии водяного пара исполь­зуются приведенные выше уравнения при условии замены величины обще­го давления кна парциальное давление углеводородовк—р ₂.

МНОГОКРАТНОЕ ИСПАРЕНИЕ И КОНДЕНСАЦИЯ

Процессы многократного испарения или конденсации со­стоят из повторяющихся в несколько ступеней процессов однократного испарения или конденсации с отводом паров и жидкости после каждой ступени (см. рис. Ill-1). При этом могут быть получены несколько продук­тов, в различной степени обогащенных НКК.

Процесс многократного испарения (конденсации) бинарной смеси можно наглядно проанализировать при помощи графика изобарных темпе­ратурных кривых и энтальпийной диаграммы.

Пусть многократному испарению (рис. Ш-4) подвергается жидкость с

содержанием НКК x_F,находящаяся первоначально при температуреt_F (точкаF).

Если первое ОИ произвести при температуре t_uто будут получены составы жидкой и паровой фаз х, и у,. При этом доля отгона на первой ступени составит

_л - * 1 -Щ^С\ - ^w\ ^с\

^с\»

У\ - ^х\ Щ ^D\ щ ^d\

а относительное количество неиспарившейся жидкости

У\ - ^х\ ^w\ ^Di ^wi ^d\

Если масса исходной жидкости составляла F,то после первой ступени ОИ масса жидкого остатка будет равна

д - р_г — р У\ ~ ^XF _ р Cj Dj -- р ^С1 ^dl У\ - *1 Щ ^D\ ^w\ <k

Жидкий остаток после первой ступени ОИ подвергают однократному испарению во второй ступени при температуре t₂.Образовавшаяся паровая и жидкая фазы будут иметь составых₂и у₂.

оз

Доля отгона на второй ступени ОИ будет равна

Рис. III-4. Графическое представление процесса многократного испарения бинарной смеси

„ _ *1-*2_^W2 ^С2_^W2^C2

^с2 -

У2 - ^х2^W2°2 ^W2^d2 а доля неиспарившейся жидкости

У2 - *2

У 2 ~ ^х\ — ^2^2 — ^c2^d2

= 1 - е

У2 ~^х2 ^W2°2 ^w2^d2

Масса жидкого остатка, полученная на второй ступени ОИ равна

У'у ~ Хг C-yDsy ^C2^d2

g-i = дд2 = д . ——- = д\ т^Чг- = ?•

w₂D₂

^2^d2

или

д₂ = g_t г₂=ftjг₂ =р( 1 - е,)(l - е₂).

После третьей ступени испарения при температуре t₃доля отгона равна

„ * ^х2 “*3 _ ^W3^C3 -^W3^C3

^е3 -

Уз ~^х3 ^W3°3 ^w3^d3

доля неиспарившегося остатка

г. _ 1_лУз ~ ^х2 _C₃D₃ __c₃d₃

i₃ — i— с₃ ,

Уз - *3 ^W3^D3 ^w3^d3 а масса оставшейся жидкости

9з = 9₂^гз = ^ ЬЬ = ^F(l - ^ei )(l - e₂)(l - е₃).

Продолжая аналогичные рассуждения, получим, что после проведения кступеней однократного испарения масса жидкости составит

я. ='Т[(>-4

Г = 1 1=1

Поскольку г, = ^1 - е, ) < 1, то увеличение числа ступеней ОН приводит

к уменьшению массы остатка в каждой последующей ступени.

В рассматриваемом примере температура третьей ступени испарения t₃ (рис. Ш-4) равна температуре полного однократного испарения жидкости с той же начальной концентрацией НКК, равнойx_F.В условиях трехкратно­го испарения такая жидкость не переходит полностью в паровую фазу и вес оставшейся жидкости равенд₃.Следовательно, при нагреве до одной и той же температуры в условиях однократного испарения обеспечивается большая доля отгона, чем при многократном испарении.

Очевидно, что для достижения одинаковой доли отгона в условиях од­нократного испарения требуется более низкая температура, чем при мно­гократном испарении; при этом остающаяся после однократного испаре­ния жидкая фаза будет содержать больше НКК, чем жидкий остаток той же массы, полученный при многократном испарении. Таким образом, при многократном испарении обеспечивается лучшее разделение компонентов, чем при однократном испарении. Процесс многократного испарения мо­жет осуществляться при температурах выше температуры полного одно­кратною испарения t₃и продолжен вплоть до температуры кипения чисто­го ВКК, равнойt_w.Однако выход достаточно чистого ВКК будет весьма мал.

Как видно из рис. Ш-4, течение процесса многократного испарения характеризуется линией WC_{WJC₂W₂C₃W₃.Увеличение числа ступеней ис­парения графически характеризуется уменьшением площадокWC_lW_] , w;C₂W₂,W₂C₃W₃.

При бесконечно большом числе ступеней испарения эти площадки превратятся в точки и течение процесса испарения изобразится перемеще­нием из точки Wв точкуW₃по кривой кипения. Такой процесс является процессомпостепенного испарения.

На энтальпийной диаграмме (рис. Ш-4) процесс трехкратного испаре­ния изобразится ступенчатой линией wc_] WjC₂w₂c₃w₃.

Рассмотрим процесс многократной конденсации (рис. Ш-5). При охлаждении паров с начальной концентрацией НКК y_Fот температурыt_F (точкаF]до температуры произойдет их частичная конденсация. Масса парового остатка будет равна

G, = Fe, = F^у— ^X-±=F=F^L£x.,

У i-X|W,D,Wi<*,

Рис. III-5. Графическое представление процесса многократной конденсации бинарной смеси

У2 -*2

На второй ступени этот паровой остаток охлаждается от температуры до температуры t₂,в результате чего часть паров вновь сконденсируется. При этом остаток паров

G₂ = G,e₂ = G, ^ = G, = F

w₂d₂

ЩС\

W,D,

W₂C₂ _

w₂d₂

= F-^ .^ ₌ Fee = F(1 - r )(1 - r ).

^1^d1^w2^d2¹²12

Паровой остаток после &-й ступени однократной конденсации составит

^с.=^рй^е.^ПН)-

1=1 i=l

Поскольку е, = - г, ) < 1 _гто увеличение числа ступеней ОК приводит

к уменьшению массы остатка в каждой последующей ступени.

Процесс многократной конденсации можно проводить вплоть до t_a — температуры кипения НКК_Годнако выход НКК высокой степени чистоты будет мал.

При сопоставлении однократной и многократной конденсации сооб­ражения, аналогичные предыдущим, позволяют сделать следующие вы­воды.

При одинаковой конечной температуре конденсации вес конденсата при однократном процессе больше, чем при многократной конденсации. При одинаковой степени конденсации конечная температура процесса в условиях однократной конденсации выше, чем при многократной конден­сации, и потому концентрация НКК в остатке паров меньше.

Процесс конденсации в три ступени на графике изобарных темпера­турных кривых характеризуется ступенчатой линией DC^ D_lC₂D₂C₂D₂.С увеличением числа ступеней конденсации площадкиDQЦ ,D(C₂D₂иD₂C₂D₂уменьшаются и при бесконечном числе ступеней они превращают­ся в точки. Течение процесса в этом случае изобразится перемещением из точкиDв точкуD₃по кривой конденсации. Такой процесс называется ло-степенной конденсацией.

Процесс трехкратной конденсации на энтальпийной диаграмме харак­теризуется ступенчатой линией dc,d_] c₂d₂c₃d₂.

ПОСТЕПЕННОЕ ИСПАРЕНИЕ (КОНДЕНСАЦИЯ)

Бинарные смеси. Рассмотрим постепенное испарение бинарной системы. Пусть в какой-то произвольный момент времени масса загрузки в испарителе будет д, а концентрация НКК в ней х, При бесконечно малом изменении температуры часть жидкости dgиспарится, а состав жидкой фазы изменится на величинуdxи станет равным х —dx. При этом образуется паровая фаза состава у.

Уравнение материального баланса по НКК для такого элементарного процесса запишется следующим образом:

дх = ydg+ {д -dg)[x-dx).

Отбросив бесконечно малые второго порядка, после преобразований получим

dg _ dx

д У ~ ^х

Проинтегрировав это дифференциальное уравнение в пределах от на­чального состояния системы Fиx_Fдо некоторого промежуточного состоя­ниядих, получим

(IIIЛ 9)

Это уравнение носит название уравнения Рейлея,

Поскольку образующиеся в процессе постепенного испарения пары состава у находятся в равновесии с жидкостью состава х, то, заменив у в уравнении (III. 19) согласно уравнению равновесия

4 - 1Я К)

97

У =

Fxp-g* ₌ ^Fxf - я^х р-д о

и проинтегрировав, получим

+ 1

(а - l|x

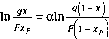
(III.20)

В таком виде уравнение Рейлея используется для определения средней величины коэффициента относительной летучести а по результатам посте­пенной перегонки.

Из материального баланса постепенной перегонки определяются сред­ний состав отогнанного продукта (фракции)

_ Я>^х> _ 9,^хI -9i₊iXj₊\

Я, -9i+\ Д

и средний состав отгона

У о ~

Аналогичный анализ может быть проведен и для процесса постепен­ной конденсации.

Материальный баланс процесса для бесконечно малой массы сконден­сированных паров запишется следующим образом:

Gy = xdG + (G - dG)(y + cfy).

Отсюда получим следующее дифференциальное уравнение:

dG _ dy ~G ~ у - x ‘

Проинтегрировав это уравнение в пределах от F и y_F до G и у, получим

I

dG

G

у

Г dy J у - х Ур

или (F >G; у_F < у)

dy

у- х

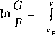
Если принять во внимание состояние равновесия между паровым остатком состава у и конденсатом состава х, то после интегрирования получим

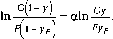
Это уравнение также может быть использовано для определения сред­ней величины коэффициента относительной летучести в интервале темпе­ратур конденсации.

Средний состав образовавшегося конденсата (жидкой фракции) оп­ределяется из материального баланса процесса постепенной конденса­ции:

для жидкой фракции

v — 6f| У/ ^— б, +1 У Г +1 .

^Ам-1 I

6, - Q+i

для всего конденсата

_ Fy р ~ Gy _ Fyp - Gy ^w F-G W

Из полученных уравнений определяются массы неиспарившейся жид­кости дпри постепенном испарении и нескоцденсировавшихся паровG при постепенной конденсации.

Многокомпонентные смеси. При постепенном испарении многоком­понентной смеси происходит постепенное изменение ее состава по мере увеличения температуры перегонки.

Обозначим число молей жидкости в произвольный момент времени

через д\а то же для 1-го компонента — черезд*, тогда

<7' = £д;-

1=1

При бесконечно малом изменении температуры жидкости образуется масса паров

dg' = Y^dg’

1-1

и соответствующие порции компонентов dg_{перейдут из жидкой в паро­вую фазу. Концентрации любого компонента будут равны: в паровой фазе

v' -^d3i_^d$;.

^У' " dg' ¹

dg;

/-1

в жидкой фазе

. / _ Qj Qj

i~~_п~ '

1=1

При этом образовавшиеся пары будут находиться в равновесии с жидкостью, т.е.

= K_tх;

Yi

Приняв во внимание вышеприведенные уравнения, получим

Проинтегрировав это дифференциальное уравнение в пределах от

-0- = к SL

dg' ' g'

f

Щ- = к_{

9l

dg'

F(дод'и отF'дод\получим его решение в следующем виде (при постоянной величинеК,}: lnii-= к in£l.

F’ F’

¹ i

Аналогичное уравнение можно записать и для другого к-го компонента смеси

ln-^- =КЛп—.

с* F'

Приняв во внимание, что коэффициент относительной летучести z-го компонента по сравнению ск-м

а

i.k

К

к

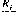
Г

придем к следующему уравнению:

In —— = а_а1п

F!

F'

^гк

Если обозначить мольную долю отгона в дистиллят через

е' = 1-£-, F'

то

д; =F'(l-e')x;, g'=F'(l-e'), F' =F%_f,

(* - ^е'К 1 0 - ^е')^х*

= a,_itln^v

и уравнение (III.21) можно представить в виде

In

*i.F

^xk,F

Это же уравнение можно использовать для расчета постепенной кон­денсации, имея в виду, что при конденсации 1 -е' = г'есть доля конденса­ции исходных паров, а начальный состав жидкостих'по любому компо­ненту определяется из условия равновесия с исходным паромy\_F.

Концентрации компонентов смеси x'_iдолжны удовлетворять уравне­нию изотермы жидкой фазы

п

Обычно предварительно задаются температурой конца процесса, определяющей величины Р₍, затем по уравнению (III.22) определяют составы

х\при заданныхеих'_ки проверяют их на соответствие уравнению изотермы жидкой фазы.

Для бинарной смеси уравнение (III.22) приводится к виду

(l-eV fl-e'Yl-x')

In^=CClnА А1,

x'_F 1 - Хр

т. е. к виду, аналогичному уравнению (III.20).