Вопросы и задания

3.17. При помощи таблиц соответствия проверьте, какие из следующих выражений являются верными тождествами:

а) ;

б) ;

в) ;

г) .

4. Примеры практического приложения булевой алгебры. Переключательные схемы

Математический аппарат булевой алгебры нашел широкое применение при проектировании технических устройств различной природы – электрических, механических, пневматических, электромагнитных, электронных, гидравлических и многих других.

В качестве примера рассмотрим электрическую схему, состоящую из источника напряжения (батареи), лампочки и одного или двух ключей (х₁их₂). Ключи управляются кнопками с двумя состояниями: 1 (кнопка нажата) и 0 (кнопка отпущена). Если в исходном состоянии ключ разомкнут, то при нажатии кнопки он замыкается (такой ключ –нормально разомкнутый). Ключ может быть сконструирован и так, что в исходном состоянии он замкнут (нормально замкнутыйключ), тогда нажатие кнопки означает его размыкание, т.е. приводит к противоположному результату. Поэтому нормально замкнутые ключи обозначим черези.

При соответствующих состояниях кнопок лампочка принимает одно из двух состояний: горит (1) и не горит (0). Состояния кнопок отождествляются со значениями булевых переменных х₁их₂, а состояние лампочки – со значениями функцииf(x₁,х₂) этих переменных.

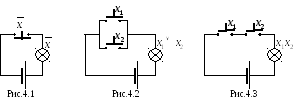
Операции отрицания соответствует переключательная схема с одним нормально замкнутым ключом (рис.4.1). Если кнопка нажата (х=1), ключ размокнут и лампочка не горит, т.е.f(x)=0; при отпущенной кнопке (х=0) ключ замкнут и лампочка горит, т.е.f(x)=1.

Операциям дизъюнкции и конъюнкции соответствуют схемы с двумя нормально разомкнутыми ключами (рис.4.2, 4.3). Легко убедиться, что в схеме на рис.4.2 лампочка горит при нажатии хотя бы одной из кнопок, а в схеме на рис.4.3 – только при нажатии обеих кнопок одновременно.

Любую булеву функцию, даже самую сложную, можно представить переключательной схемой.

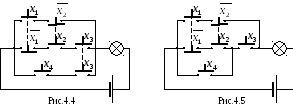
На рис.4.4 показана схема, реализующая функцию . Та же функция представляется равносильной формулой, которой соответствует более простая схема (рис.4.5). Следует иметь ввиду, что ключи, обозначенные одинаковыми буквами (например,х₁и), связаны между собой и управляются общей кнопкой, так как они описываются одной и той же переменной.

Вопросы и задания

4.1. Постройте переключательные схемы, соответствующие следующим функциям:

а) ;

б) .

5. Тождественные преобразования

Как видно на рис.4.4 и рис.4.5, одна и та же булева функция может быть реализована различными переключательными схемами и описана разными формулами. Далее рассмотрим правила тождественного преобразования булевых функций.

На основании таблиц соответствия нетрудно убедиться в справедливости следующих тождеств (свойств) булевой алгебры:

1) коммутативность:

;

2) ассоциативность:

;

3) дистрибутивность:

;

4) свойство констант:

;

5) свойство отрицания:

.

Рассмотрим для примера доказательство первого из законов дистрибутивности с помощью таблицы соответствия. Для этого построим таблицы соответствия для левой и правой частей предполагаемого тождества (см.табл.5.1).

Таблица 5.1
х	у	z
0	0	0	0	0	0	0	0
0	0	1	1	0	0	0	0
0	1	0	1	0	0	0	0
0	1	1	1	0	0	0	0
1	0	0	0	0	0	0	0
1	0	1	1	1	0	1	1
1	1	0	1	1	1	0	1
1	1	1	1	1	1	1	1

Как видно из табл.5.1, значения левой и правой части (выделены жирным шрифтом) совпадают при всех значениях переменных, что и требовалось доказать.

Аналогично, путем построения таблиц соответствия, могут быть доказаны и другие приведенные выше тождества.

Эти свойства позволяют получить ряд других важных законов и тождеств уже без обращения к таблицам соответствия:

1) законы де Моргана:

;

2) законы поглощения:

;

3) законы идемпотентности:

.

Докажем справедливость первого из законов де Моргана. Для этого равенство путем последовательных преобразований сведем к очевидному тождеству.

Из равенства и свойств отрицания следует, что

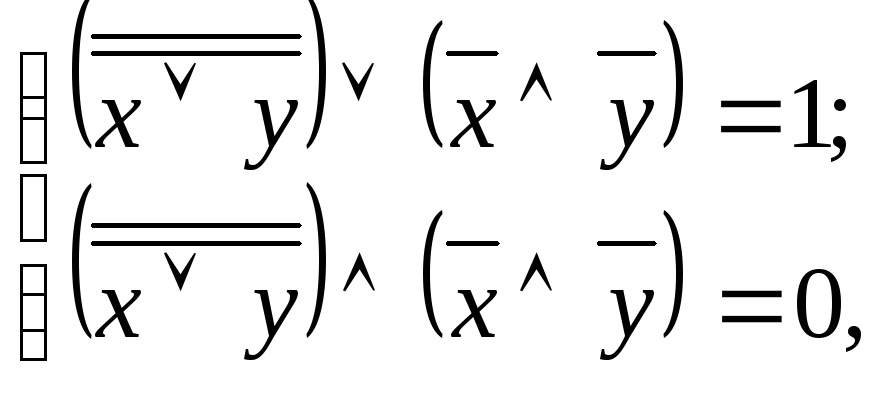
т.е.

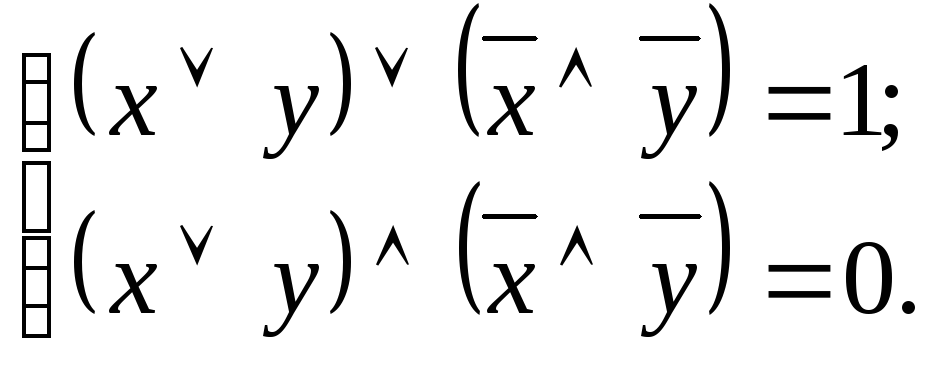
После раскрытия скобок получим следующее:

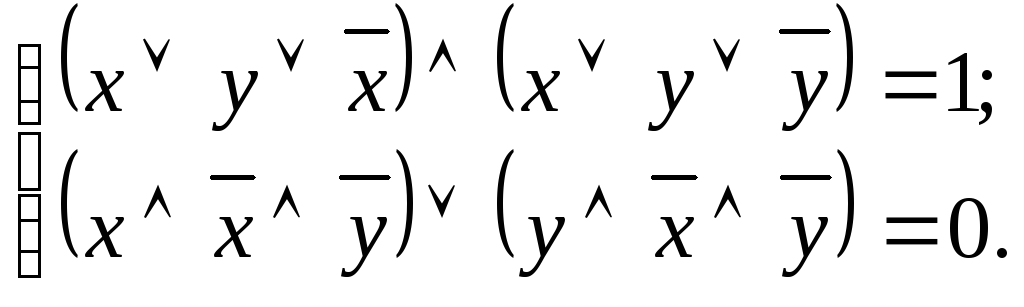
Так как и, аи, то предыдущее выражение можно представить в следующем виде:

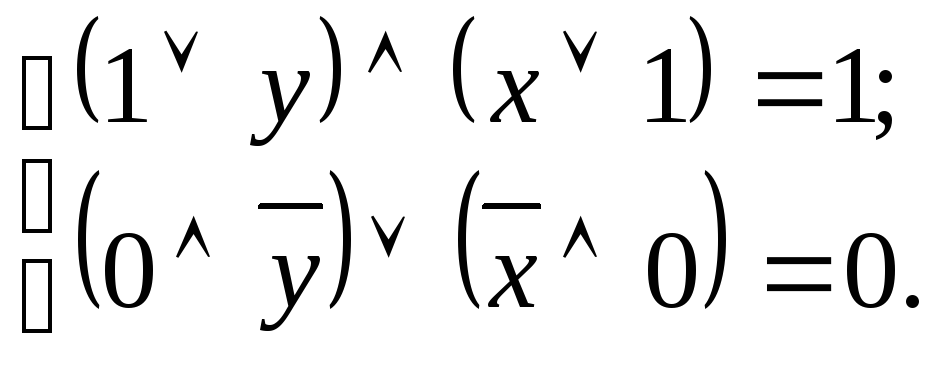
Используя свойства констант (,,,), получаем

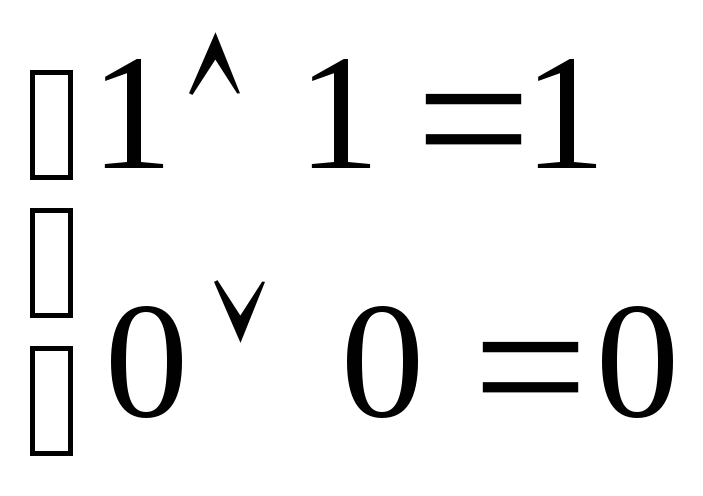–очевидное тождество.

Таким образом, путем эквивалентных преобразований мы привели выражение первого закона де Моргана к тождеству и этим доказали справедливость данного закона.

Второй закон де Моргана может быть легко получен на основе первого путем отрицания левой и правой части и соответствующей замены переменных. Запишем первый закон де Моргана относительно переменных aиb:

.

Если равны сами выражения, то равны и их отрицания:

.

Из свойств двойного отрицания:

.

Произведем замену переменных:

После замены получим:

,

т.е. второй из законов де Моргана.

Также имеют место следующие тождества:

; ;

и т.д.