
- •Самарский государственный университет
- •1. Введение в математический анализ
- •1.1. Числовая функция одной переменной.
- •1.2. Числовая функция нескольких переменных.
- •1.3. Числовая последовательность.
- •1.5. Предел числовой последовательности.
- •1.6. Предел числовой функции одной переменной.
- •1.7. Предел числовой функции нескольких переменных.
- •1.8. Бесконечно малые, ограниченные, бесконечно большие и отделимые от нуля величины.
- •1.9. Простейшие свойства бесконечно малых величин.
- •1.10. Простейшие свойства пределов.
- •1.11. Сравнение бесконечно малых величин.
- •1.12. Свойства эквивалентных бмв. Главная часть бмв и ббв.
- •1.13. Предельный переход в неравенстве. Признаки существования предела. Замечательные пределы.
- •1.14. Таблица основных эквивалентных бмв.
- •1.15. Непрерывность функций в точке.
- •1.16. Односторонние пределы и классификация точек разрыва.
- •1.17. Свойства функций непрерывных на отрезке.
- •2. Дифференциальное исчисление
- •2.1. Производная и дифференциал числовой функции одной переменной.
- •2.2. Геометрический смысл производной и дифференциала числовой функции одной переменной.
- •2.3. Сводка правил для вычисления производной.
- •2.4. Частные производные и полный дифференциал числовой функции нескольких переменных.
- •2.5. Геометрический смысл частных производных и полного дифференциала.
- •2.6. Вычисление производных и дифференциалов сложных функций.
- •2.7. Вычисление производных неявных функций.
- •2.8. Производные и дифференциалы высших порядков для числовой функции одной переменной.
- •2.9. Частные производные и полные дифференциалы высших порядков.
- •2.10. Свойства функций, дифференцируемых на интервале.
- •2.11. Раскрытие неопределенностей по правилу Лопиталя
- •2.12. Формула Тейлора.
- •2.13. Представление некоторых функций по формуле Тейлора.
- •2.14. Приложения формулы Тейлора к исследованию функций
- •2.14.1. Главная часть бм
- •2.14.2 Возрастание и убывание функции
- •2.14.3. Экстремумы функции
- •2.14.4. Выпуклость и вогнутость кривой.
- •2.14.5. Точки перегиба кривой.
- •2.15. Формула Тейлора для числовой функции нескольких переменных.
- •2.16. Локальные экстремумы функции нескольких переменных.
- •2.17. Аппроксимация опытных данных по методу наименьших квадратов.
- •2.18. Производная скалярного поля по направлению. Градиент.
- •2.19. Условные экстремумы числовой функции нескольких переменных.
- •2.20. Формулировка задачи линейного программирования
1.9. Простейшие свойства бесконечно малых величин.
Теорема 1. Сумма нескольких БМВ есть величина БМВ.
Доказательство:
Рассмотрим несколько
БМВ
![]() .
Для определенности пусть это будут
функции одной переменной. По определению
предела
.
Для определенности пусть это будут
функции одной переменной. По определению
предела![]() будем иметь
будем иметь
 .
.
Обозначим
![]() .
Тогда
.
Тогда
![]() .
.
Следовательно
![]()
и
![]() БМВ, что и требовалось
доказать.
БМВ, что и требовалось
доказать.
Теорема 2. Произведение БМВ на ограниченную величину есть БМВ.
Доказательство:
Для
доказательства выберем любое число
![]() .
Если
.
Если![]() ,
то можно считать, что
,
то можно считать, что![]() .
Тогда
.
Тогда
![]() .
.
Следовательно
![]() – БМВ, что и требовалось доказать.
– БМВ, что и требовалось доказать.
1.10. Простейшие свойства пределов.
Теорема 1. Если
величины
![]() имеют конечные пределы, то
имеют конечные пределы, то
![]() .
.
Доказательство:
Обозначим
 .
.
Тогда
![]() .
.
Здесь
![]() – БМВ. Поэтому
– БМВ. Поэтому![]() ,
что и требовалось доказать.
,
что и требовалось доказать.
Теорема 2. Если
величины
![]() имеют конечные пределы, то
имеют конечные пределы, то
![]()
Доказательство:
 .
.
Что и требовалось доказать.
Теорема 3. Если
величины
![]() имеют конечные пределы, причём
имеют конечные пределы, причём![]() ,
то
,
то
![]() .
.
Доказательство:
Отметим, что
величина
![]() отделима от нуля, и поэтому отношение
отделима от нуля, и поэтому отношение![]() определено в соответствующей области.
определено в соответствующей области.
 ,
,
![]() .
.
Что и требовалось доказать.
1.11. Сравнение бесконечно малых величин.
Все бесконечно
малые величины в соответствующей области
стремятся к нулю, при этом они могут
стремиться к нулю с разными «скоростями».
Например, при
![]() три функции
три функции![]() являются БМВ. Из рисунка видно, что
скорость приближения к оис абсцисс
различная.
являются БМВ. Из рисунка видно, что
скорость приближения к оис абсцисс
различная.

Отношение БМВ
![]() в зависимости от ситуации может стремиться
к нулю, к конечному числу или бесконечности.
Для оценки скорости стремления БМВ к
нулю введем следующие определения.
в зависимости от ситуации может стремиться
к нулю, к конечному числу или бесконечности.
Для оценки скорости стремления БМВ к
нулю введем следующие определения.
1. Величины и называются БМВ одного порядка, если существует конечный ненулевой предел их отношения
![]() (1.11.1)
(1.11.1)
2. Если
![]() , (1.11.2)
, (1.11.2)
то величины и называются эквивалентными БМВ. Обозначают эквивалентные величины
![]() . (1.11.3)
. (1.11.3)
3. Если
![]() , (1.11.4)
, (1.11.4)
то величину называют БМВ высшего порядка по отношению к величине . Обозначают этот факт
![]() . (1.11.5)
. (1.11.5)
4. Величина
называется БМВ
п-го
порядка
по отношению к величине ,
если
и
![]() есть БМВ одного порядка
есть БМВ одного порядка
![]() (1.11.6)
(1.11.6)
5.
Если предел отношения
![]() не существует или его трудно вычислить,
но само отношение есть ограниченная
величина
не существует или его трудно вычислить,
но само отношение есть ограниченная
величина
![]() , (1.11.7)
, (1.11.7)
то обозначают этот факт так
![]() . (1.11.8)
. (1.11.8)
Аналогичные понятия можно ввести и для сравнения скорости роста ББВ.
1.12. Свойства эквивалентных бмв. Главная часть бмв и ббв.
Теорема
1. Если
![]() ,
то
,
то![]() .
.
Доказательство:
![]() .
.
Теорема
2. Если
![]() ,
то
,
то![]() .
.
Доказательство:
![]() .
.
Теорема 3. Предел отношения двух БМВ равен пределу отношения БМВ, эквивалентных заданным.
Доказательство:
 .
.
Пусть БМВ представлена в виде суммы нескольких БМВ
![]() , (1.12.1)
, (1.12.1)
причем
![]() .
Тогда самое крупное слагаемое
.
Тогда самое крупное слагаемое![]() называетсяглавной
частью
БМВ.
называетсяглавной
частью
БМВ.
Главная часть БМВ определяется неоднозначно. Например,
![]() . (1.12.2)
. (1.12.2)
Теорема 4. БМВ эквивалентна своей главной части.
Доказательство:
![]() .
.
В качестве иллюстрации рассмотрим два примера.
![]() .
.
![]() .
.
1.13. Предельный переход в неравенстве. Признаки существования предела. Замечательные пределы.
Теорема 1 (о
предельном переходе в неравенстве).
Если величины
![]() и
и![]() имеют пределыа
и b
(соответственно),
то при
имеют пределыа
и b
(соответственно),
то при
![]() справедливо неравенство
справедливо неравенство![]() .
.
Доказательство:
Доказательство
проведем от противного, предположив,
что ![]() .
Тогда,
.
Тогда,
![]() .
Выберем
.
Выберем![]() ,
тогда в соответствующей области будем
иметь
,
тогда в соответствующей области будем
иметь
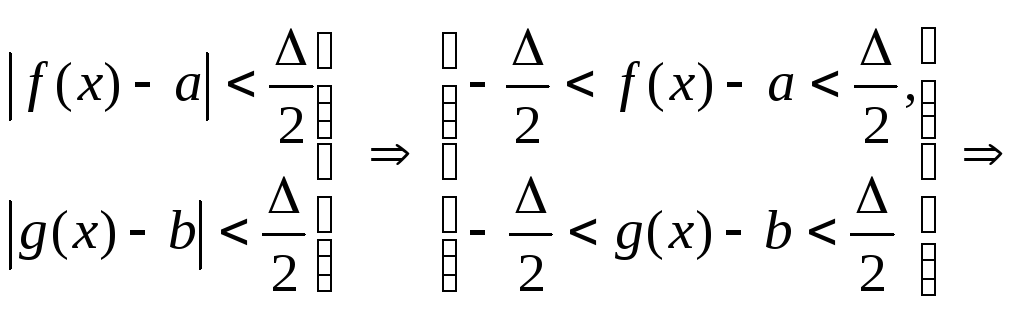
![]() .
.
Последнее
неравенство противоречит условию
теоремы, значит
![]() ,
что и требовалось доказать.
,
что и требовалось доказать.
Отметим, что в
случае строгого неравенства для функций![]() нельзя получить строгое неравенство
для пределов
нельзя получить строгое неравенство
для пределов![]() .
Действительно,
.
Действительно,
![]() .
.
Теорема 2 (Первый признак существования предела). Величина, заключенная между двумя другими величинами, имеющими один и тот же конечный предел, имеет тот же самый предел
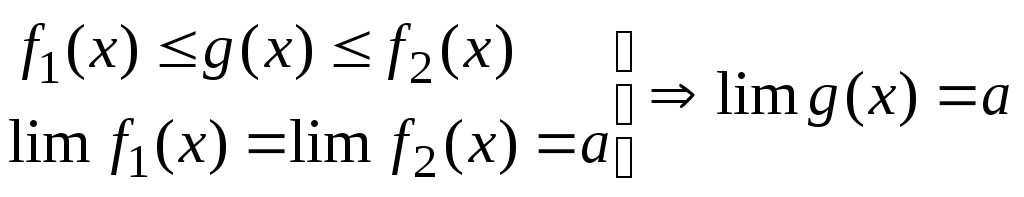 .
.
Доказательство:
![]() имеем
имеем

![]() .
.
Теорема 3 (Первый замечательный предел).
![]() . (1.13.1)
. (1.13.1)
Доказательство:
Из рисунка

видно, что
![]() ,
,
![]() ,
,
![]() ,
,
![]() или
или
![]() ,
,
так как
![]() ,
,
окончательно получаем
![]() .
.
Что и требовалось
доказать. Таким образом, при
![]()
![]() .
.
Дадим следующее определение.
Монотонно возрастающей переменной называется:
Числовая последовательность, если
 при
при .
.Числовая функция одной переменной, если
 .
.
Аналогично вводится понятие монотонно убывающей переменной.
Теорема 4 (Второй признак существования предела, теорема Вейерштрасса).
Всякая монотонно возрастающая ограниченная переменная имеет конечный предел.
(Без доказательства)
Теорема 5 (Второй замечательный предел)
![]() . (1.13.2)
. (1.13.2)
Можно показать, что
![]() ,
,
и
![]() .
.
Таким образом по теореме 4 второй замечательный предел существует. Его обозначают буквой e и называют числом Непера (это иррационально число, e=2.718281828…).
Существует еще две модификации второго замечательного предела
![]() , (1.13.3)
, (1.13.3)
и
![]() . (1.13.4)
. (1.13.4)
