2.18. Производная скалярного поля по направлению. Градиент.

Рассмотрим дифференцируемую функцию трех переменных (скалярное поле) . Каждая из ее трех частных производных

характеризует скорость роста функции в направлении координатных осей.

Выясним, какая величина характеризует скорость роста этого скалярного поля в направлении произвольной прямой.

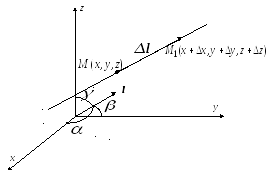
Рассмотрим произвольную прямую в пространстве, направление которой задается единичным вектором .

Возьмем на прямой точку и точку . Эти точки образуют вектор , коллинеарный вектору.

Полное приращение функции

выражается через частные производные формулой (2.4.13)

,

или

. (2.18.1)

Разделим обе части равенства (2.18.1) на

.

Учитывая, что

,

находим

. (2.18.2)

Если существует предел

, (2.18.3)

то этот предел называется производной скалярного поля по направлению вектора .

Переходя в равенстве (2.18.2) к пределу при , получаем формулу для вычисления производной по направлению

. (2.18.4)

Три частных производных в качестве координат образуют вектор

, (2.18.5)

который называется градиентом скалярного поля в рассматриваемой точке .

Очевидно, что вектор – градиент и производная по направлению связаны соотношением

. (2.18.6)

Обозначим угол между векторами и – . Тогда

. (2.18.7)

Формула (2.18.7) показывает, что максимальное значение производной по направлению соответствует углу . Таким образом, вектор градиента указывает в пространстве направление максимального возрастания скалярного поля. Уголсоответствует направлению максимального убывания скалярного поля. Уголсоответствует направлению, в котором скалярное поле не изменяется.

Если рассмотреть поверхности уровня , на которых скалярное поле постоянно, то уравнение касательной плоскости к такой поверхности в точкеимеет вид

.

Частные производные выражаются через частные производныепо формула производных неявных функций

, .

Тогда уравнение касательной плоскости принимает вид

.

Главным вектором этой касательной плоскости является вектор градиента, следовательно, градиент направлен по нормали к поверхности уровня.

2.19. Условные экстремумы числовой функции нескольких переменных.

Пусть функция двух переменных выражает в количественном отношении некоторую цель (прибыль фирмы, транспортные расходы, производственные издержки и т.д.). Эта функция так и называется –целевая функция. Обычных локальных экстремумов эта функция может не иметь. На ее аргументы (обычно в их роли выступают некоторые ресурсы – закупаемое сырье, стоимость перевозок, зарплата работникам, электроэнергия, износ оборудования и т.д.) накладываются некоторые ограничения, которые связывают их функциональной зависимостью . Таким образом, формулируется задача отыскания экстремумов целевой функции при наложенных на аргументы ограничениях.

. (2.19.1)

Такие экстремумы называютсяусловными экстремумами.

Если уравнение можно разрешить относительно переменнойy, то поиск условного экстремума сведется к поиску обычного экстремума для функции одной переменной . Однако, как правило, решить нелинейное уравнение аналитически невозможно, поэтому для поиска условных экстремумов разработан специальный алгоритм –метод множителей Лагранжа.

Продифференцируем как сложную функцию, учитывая, что

.

Необходимое условие экстремума , дает

. (219.2)

Выражая из уравнения (2.19.2) производную , находим

. (2.19.3)

Вычислим теперь эту же производную как производную функции заданную неявно уравнением

. (2.19.4)

Сравнивая производные (2.19.3) и (2.19.4), получаем равенство

,

равносильное системе двух уравнений

.

Присоединяя к этой системе ограничение , получаем замкнутую систему уравнений

, (2.19.5)

относительно неизвестных . Решением системы (2.19.5) и будут условные экстремумы поставленной задачи.

Систему (2.19.5) легко получить с помощью вспомогательной функции Лагранжа

. (2.19.6)

Очевидно, что необходимые условия для обычных локальных экстремумов для функции Лагранжа (2.19.6) приводят нас снова к системе (2.19.5)

. (2.19.7)

Совершенно аналогично решается задача нахождения условных экстремумов в общем случае, когда целевая функция является функцией нескольких переменных, а на аргументы накладывается несколько условий. Задача отыскания условных экстремумов формулируется следующим образом

. (2.19.8)

Функция Лагранжа для такой задачи имеет вид

. (2.19.9)

Параметры называютсямножителями Лагранжа.

Пример. Найти кратчайшее расстояние от начала координат до кривой

.

Решение:

Целевая функция здесь имеет вид

.

Составляем функцию Лагранжа

.

Записываем необходимые условия локальных экстремумов

.

Из двух первых уравнений системы, находим

.

Исключаем из системы переменную .

Окончательно находим

.

Из рисунка видно, что в первой точке целевая функция достигает максимума, а во второй – минимума, причем

, .