Задание 4.10.

Фирма, изготовляющая деревянную продукцию, производит два вида обшивочных панелей: колониальную и западную. Производство панелей осуществляется двумя операциями: прессованием и отделкой. Задача администрации фирмы — узнать, сколько пластов обоих типов обшивочной панели нужно производить в месяц, чтобы получить максимальную прибыль.

Проблема в том, что продукция панелей ограничена — фирма ограничена средствами для производства продуктов. Задача состоит в оптимальном размещении средств для получения наибольшей прибыли.

Фирма обладает ресурсами в условиях доступности леса, имеется достаточно рабочих часов для прессования и обработки, а также долларовый бюджет.

Ресурсные потребности и возможности для каждого типа панелей, которые образовывают параметры модели, смотрите в таблице.

	Необходимые средства для партии из 100 пластов обшивочной панели		Всего средств в месяц
Средства	Колониальные	Западные
Деревянная продукция	20 кг	40 кг	4000 кг
Прессование	4 ч.	6ч.	900 ч.
Отделка	4 ч.	4 ч.	600 ч.
Стоимость	$ 30	$ 50	$ 6000

Фирма получает 80 дол. прибыли за каждые 100 пластов колониальной панели и 100 дол. – за каждые 100 пластов западной панели.

Задание 4.11.

В трех пунктах отправления сосредоточен однородный груз в количествах, равных 420, 380 и 400 т. Этот груз необходимо перевезти в три пункта назначения в количествах, соответственно равных 260, 520 и 420 т. Тарифы перевозок 1 т груза из каждого пункта отправления в каждый пункт назначения являются известными величинами и задаются матрицей

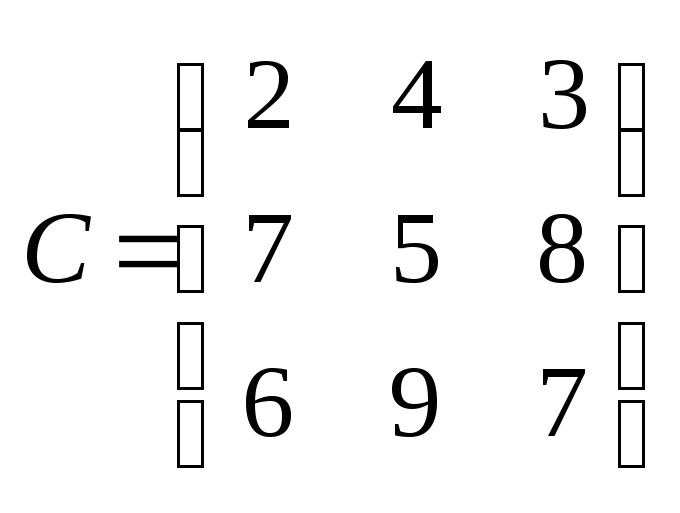
Найти план перевозок, обеспечивающий вывоз имеющегося в пунктах отправления и завоз необходимого в пунктах назначения груза при минимальной общей стоимости перевозок.

Задание 4.12.

Четыре предприятия для производства продукции используют три вида сырья. Потребности в сырье каждого из предприятий соответственно равны 120, 50, 190 и 110 ед. Сырье сосредоточено в трех местах его получения, а запасы соответственно равны 160, 140, 170 ед. На каждое из предприятий сырье может завозиться из любого пункта его получения. Тарифы перевозок являются известными величинами и задаются матрицей

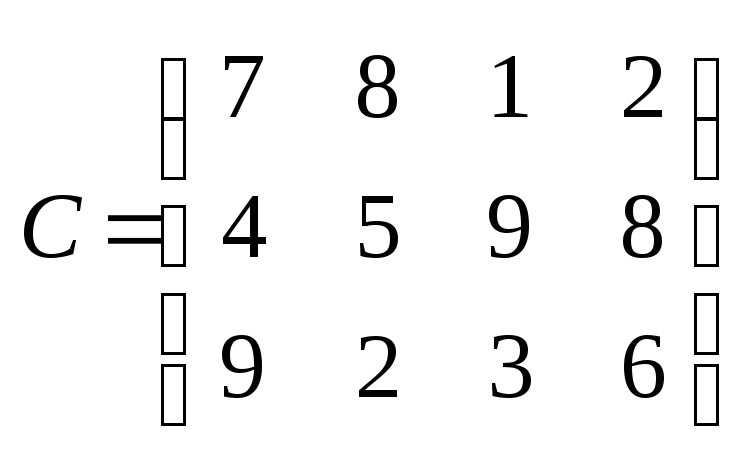
Составить такой план перевозок, при котором общая стоимость перевозок является минимальной.

Задание 4.13.

На трех складах оптовой базы сосредоточен однородный груз в количествах 90, 60 и 150 ед. Этот груз необходимо перевезти в четыре магазина. Каждый из магазинов должен получить соответственно 120, 40, 60 и 80 ед. груза. Тарифы перевозок единицы груза из каждого из складов во все магазины задаются матрицей

Составить такой план перевозок, при котором общая стоимость перевозок является минимальной.

Задание 4.14.

Производственное объединение имеет в своем составе три филиала, которые производят однородную продукцию соответственно в количествах, равных 50, 30 и 10 ед. Эту продукцию получают четыре потребителя, расположенные в разных местах. Их потребности соответственно равны 30, 30, 10 и 20 ед. Тарифы перевозок единицы продукции от каждого из филиалов соответствующим потребителям задаются матрицей

Составить такой план прикрепления получателей продукции к ее поставщикам, при котором общая стоимость перевозок является минимальной.