
Тесты по высшей математике-2 часть Функция одной переменной (14 тестов)
3.1.1.1/1
Значение функции у=2х3-5 в точке х=2 равно
Ответ 11
УС 1
Время 0.5
3.1.1.1/2
Значение функции у=3х4-10 в точке х=1 равно
Ответ -7
УС 1
Время 0.5
3.1.1.2/1
Периодической функцией является
1.![]() +2.
+2.
![]() 3.
3.
![]() 4.
4.
![]()
УС 1
Время 0.5
3.1.1.3/1
Четными функциями являются:
+1.![]() +2.
+2.
![]() 3.
3.
![]() 4.
4.
![]()
УС 1
Время 1
3.1.1.3/2
Нечетными функциями являются:
+1.![]() 2.
2.
![]() 3.
3.
![]() +4.
+4.
![]()
УС 1
Время 1
3.1.1.4/1
Постоянной функцией является
1.
![]() 2.
2.
![]() +
3.
+
3.
![]() 4.
4.
![]()
УС 1
Время 0.5
3.1.1.5/1
Ограниченной на всей действительной оси функцией является:
1.![]() +2.
+2.
![]() 3.
3.
![]() 4.
4.
![]()
УС 1
Время 1
3.1.2.1/1
Наименьшее целое из области определения степенной функции равно
1.![]() 2.
2.
![]() 3.
3.
![]() 4.
4.
![]() .
.
Ответ
![]()
УС 2
Время 1
3.1.2.3/1
Наибольшее целое из области определения логарифмической функции
1.
![]() 2.
2.
![]() 3.
3.
![]() 4.
4.
![]() .
.
Ответ 0
УС 2
Время 1
3.1.2.2/1
Наименьшее целое из множества значений показательной функции равно
1.
![]() 2.
2.
![]() 3.
3.
![]() 4.
4.
![]()
Ответ 1
УС 2
Время 1
3.1.2.4/1
Значение тригонометрической функции
![]() ,
соответствующее
,
соответствующее
![]() равно
равно
Ответ 0
УС 2
Время 1
3.1.2.5/1
Значение обратной тригонометрической
функции
![]() ,
соответствующее
,
соответствующее
![]() равно
равно
Ответ 2
УС 2
Время 1
3.1.2.5/2
Значение обратной тригонометрической
функции
![]() соответствующее
соответствующее
![]() равно
равно
Ответ 4
УС 2
Время 1
3.1.2.6/1
Соответствие названий и аналитических выражений гиперболических функций
1 пара .гиперболический синус ![]()
2 пара .гиперболический косинус ![]()
3 пара . гиперболический тангенс ![]()
4 пара . гиперболический котангенс ![]()
УС 2
Время 1
Предел функции, непрерывность , разрывы( 27 тестов)
3.1.3.1/1
Предел функции
![]() равен
равен
Ответ 7
УС 2
Время 1
3.1.3.1/2
Предел функции
![]() равен
равен
Ответ 9
УС 2
Время 1
3.1.3.2/1
Предел функции
![]() равен
равен
Ответ 5
УС 2
Время 1
3.1.3.2/2
Предел функции
![]() равен
равен
Ответ 0
УС 2
Время 1
3.1.3.3/1
Непрерывными на интервале [-1,2] функциями являются
+1.![]() +2.
+2.![]() 3.
3.![]() 4.
4.![]() 5.
5.![]() .
.
УС 2
Время 1
3.1.3.3/2
Непрерывными на интервале [-2,3] функциями являются
1.
![]() +2.
+2.
![]() +3.
+3.
![]() 4.
4. ![]() 5.
5.![]() .
.
УС 2
Время 1
3.1.3.3/3
Функция имеет разрыв первого рода на интервале [-3,3]
1.
![]() 2.
2.
![]() +3.
+3.
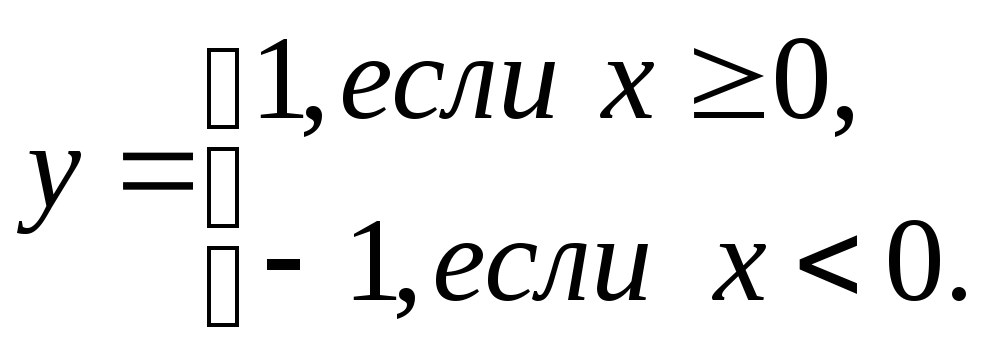 4.
4. ![]() 5.
5.![]()
УС 3
Время 1
3.1.3.3/4
Функции имеют разрывы второго рода на интервале [-1,3]
+1.
![]() +2.
+2.
![]() 3.
3.
![]() 4.
4.  +5.
+5.![]()
УС 3
Время 1
3.1.3.4/1
Бесконечно малой функцией при
![]() является:
является:
1.
![]() 2.
2.
![]() 3.
3.
![]() +4.
+4.
![]() .
.
![]()
УС 3
Время 1
3.1.3.4/2
Бесконечно большой функцией при
![]() является :
является :
1.
![]() +2.
+2.
![]() 3.
3.
![]() 4.
4.![]() .
.
![]()
УС 3
Время 1
3.1.3.5/1
Предел функции
![]() равен
равен
Ответ -5
УС 3
Время 2
3.1.3.5/2
Предел функции
![]() равен
равен
1. 3 2. 1 3. 0 +4.
![]() 5.
0.75
5.
0.75
УС 3
Время 2
3.1.3.5/3
Предел функции
![]() равен
равен
Ответ 4
УС 3
Время 2
3.1.3.5/4
Предел функции
![]() равен
равен
1. 3 2. 1 +3. 0 4.
![]() 5.
-1.5
5.
-1.5
УС 3
Время 2
3.1.3.6/1
Предел функции
![]() равен
равен
Ответ 2
УС 3
Время 1
3.1.3.6/2
Предел функции
![]() равен
равен
Ответ 10
УС 3
Время 3
3.1.3.6/3
Предел функции
![]() равен
равен
Ответ 4
УС 3
Время 3
3.1.3.6/4
Предел функции
![]() равен
равен
Ответ 2
УС 3
Время 3
3.1.3.7/1
Предел функции
![]() равен
равен
Ответ 12
УС 3
Время 1
3.1.3.7/2
Предел функции
![]() равен
равен
Ответ 2
УС 3
Время 1
3.1.3.8/1
Предел функции
![]() равен
равен
1. 3 2. 1 3. 0 4.
![]() +5.
+5.
![]()
УС 4
Время 3
3.1.3.8/2
Предел функции
![]() равен
равен
1. 4 2. 1 3. 0 +4.
![]() 5.
5.
![]()
УС 4
Время 3
3.1.3.9/1
Функции
![]() называются
эквивалентными, если предел их отношения
называются
эквивалентными, если предел их отношения
![]()
1. бесконечен 2. единица +3. ноль 4. конечное число
УС 3
Время 1
3.1.3.9/2
Предел функции
![]() равен
равен
Ответ 6
УС 3
Время 1
3.1.3.9/3
Предел функции
![]() равен
равен
Ответ 5
УС 3
Время 1
3.1.3.9/4
Предел функции
![]() равен
равен
Ответ 4
УС 4
Время 1
3.1.3.9/5
Предел функции
![]() равен
равен
Ответ 2
УС 4
Время 1
