2.2 Основные свойства определенного интеграла

Свойство 1. Постоянный множитель можно выносить за знак интеграла:

.

Доказательство:

.

Свойство 2. Интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от этих функций:

.

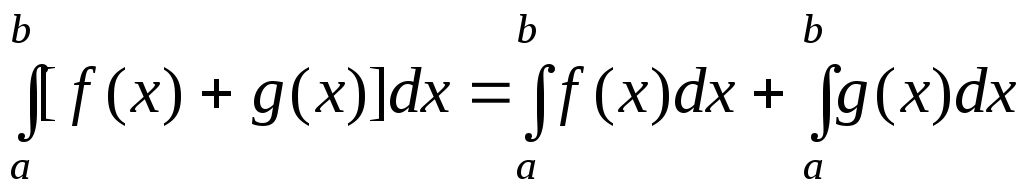Доказательство:

.

Свойство 3. Если отрезок интегрирования разбить на два отрезкаи, то интеграл по всему отрезкубудет равен сумме интегралов по отрезками:

.

Доказательство:

.

Свойство 4. При перемене местами пределов интегрирования интеграл изменяет знак:

.

Доказательство следует из определения определенного интеграла (при).

Свойство 5. Интеграл с одинаковыми пределами интегрирования равен нулю:

.

Доказательство следует из свойства 4 (при ):

.

Свойство 6. Интеграл от постоянной величины равен этой постоянной, умноженной на длину отрезка интегрирования:

.

Доказательство:

.

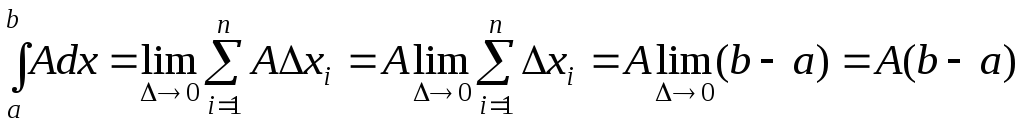Свойство 7. Если m и M – наименьшее и наибольшее значения функции на отрезке, то

.

Доказательство дается переходом к пределу при в очевидных неравенствах:

.

Свойство 8. Абсолютная величина интеграла от данной функции не превышает интеграла от абсолютной величины этой же функции:

.

Доказательство. Так как на основании свойства абсолютной величины числа для, то

откуда при переходе к пределу при получаем:

а это равносильно неравенству, которое требовалось доказать.

Свойство 9 (Теорема о среднем). Если функция непрерывна на отрезке, то на этом отрезке существует такая точкас, что справедлива формула

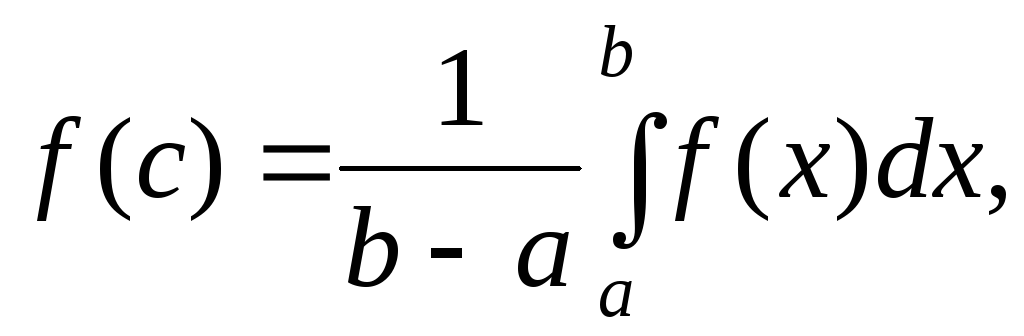
называемая формулой среднего значения функции на отрезке.

Доказательство. Так как функция непрерывна на отрезке, то по второй теореме Вейерштрасса

.

Отсюда на основании свойства 7 получаем

или

Положим

Так как функция непрерывна на отрезке, то по второй теореме Больцано-Коши на отрезкенайдется такая точкас, что . Поэтому

что и требовалось доказать.

2.3 Производная определенного интеграла по переменному верхнему пределу

Пусть на отрезке задана непрерывная функция.

Определение. Функция

называется определенным интегралом с переменным верхним пределом.

Теорема 2.2. Производная определенного интеграла от непрерывной на отрезке функции по переменному верхнему пределу равна значению подынтегральной функции на верхнем пределе:

.

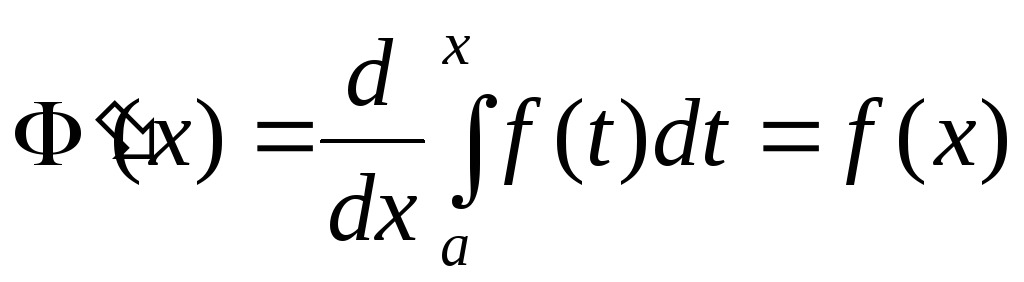Доказательство. Дадим аргументу приращение. Найдем приращение функции, используя свойство 3 определенного интеграла:

.

Применяя к последнему интегралу теорему о среднем (свойство 9), получим

,

где с заключено между и.

Согласно определению производной имеем

.

Так как , то, и в силу непрерывности подынтегральной функциина отрезке

.

Следовательно, .

Таким образом, доказана теорема 1.2 существования первообразной для непрерывной на отрезке функции, причем первообразной дляявляется определенный интеграл с переменным верхним пределом:

.

2.4 Формула Ньютона-Лейбница

С помощью теоремы 2.2 выведем основную формулу интегрального исчисления – формулу Ньютона-Лейбница. Эта формула дает способ вычисления определенного интеграла через первообразную от подынтегральной функции, не прибегая к составлению интегральной суммы и к вычислению ее предела.

Теорема 2.3. Если есть какая-либо первообразная от непрерывной на отрезке функции, то справедливаформула Ньютона-Лейбница:

.

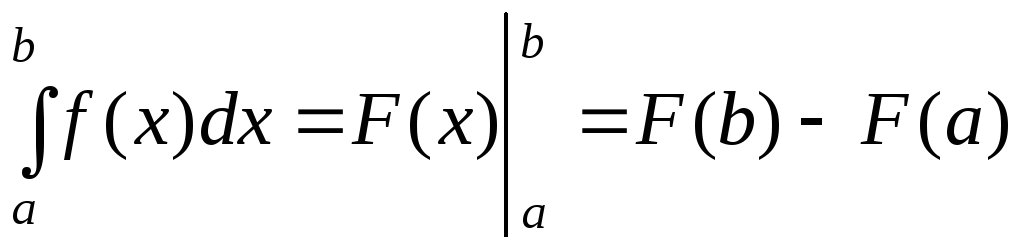Доказательство. По теореме 2.2 функция является первообразной от функциина отрезке, т.е.

.

Определим постоянную С, подставляя в это равенство значение и используя свойство 5 определенного интеграла:

, так как .

Тогда

.

Полагая в полученном равенстве и затем заменяя переменную интегрированияt на x, получаем формулу Ньютона-Лейбница.

Пример

.