1.4 Таблица основных интегралов

Приведем таблицу основных интегралов, которая непосредственно следует из определения интегрирования как операции, обратной дифференцированию, и таблицы производных. Справедливость всех формул легко проверить дифференцированием первообразных. Интегралы, содержащиеся в этой (или подобной ей) таблице, принято называть табличными.

Таблица интегралов в силу инвариантности формы дифференциала функции оказывается справедливой независимо от того, является ли переменная интегрирования независимой переменнойили любой её дифференцируемой функцией ().

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

11. .

12. .

13. .

14. .

15. .

16. .

Отметим, что если операция дифференцирования элементарных функций снова приводит к элементарным функциям, то операция интегрирования уже может привести к неэлементарным функциям, т.е. функциям, которые не выражаются через конечное число арифметических операций и суперпозиций элементарных функций.

Например, доказано, что следующие интегралы хотя и существуют, но не являются элементарными функциями:

– интеграл Пуассона;

– интегральный логарифм;

– интегралы Френеля.

1.5 Основные методы интегрирования

1. Непосредственное интегрирование. Вычисление интегралов с помощью непосредственного использования таблицы простейших интегралов и основных свойств неопределенных интегралов называется непосредственным интегрированием или методом разложения.

Пример

.

2. Метод подстановки (замены переменной). Метод, позволяющий с помощью введения новой переменной интегрирования свести нахождение данного интеграла к нахождению табличного интеграла, называется методом подстановки или методом замены переменной.

Метод основан на следующей теореме.

Теорема 1.3. Пусть функция определена и дифференцируема на некотором множествеT и пусть X – множество значений этой функции, на котором определена функция . Тогда, если на множествеX функция имеет первообразную, то на множествеT справедлива формула замены переменной в неопределенном интеграле:

.

Доказательство. Пусть – первообразная для на множествеX. Рассмотрим на множестве T сложную функцию . По правилу дифференцирования сложной функции, учитывая, что, получаем

,

т.е. функция имеет на множествеT первообразную и, следовательно,

.

Но

,

поэтому

.

Пример

.

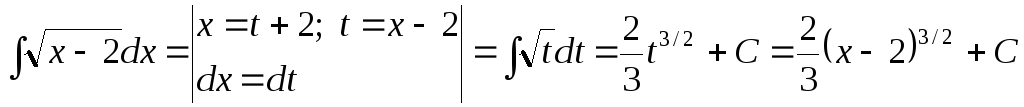Иногда формулу замены переменной полезно применять справа налево:

.

Пример

.

3. Метод интегрирования по частям. Метод интегрирования по частям основан на использовании формулы дифференцирования произведения двух функций.

Теорема 1.4. Пусть функции иопределены и дифференцируемы на некотором промежуткеX и пусть функция имеет первообразную на этом промежутке. Тогда на промежуткеX функция также имеет первообразную и справедливаформула интегрирования по частям в неопределенном интеграле:

.

Доказательство. Из равенства

получаем

.

Первообразной функции на промежуткеX является функция . Функцияимеет первообразную наX по условию теоремы. Следовательно, и функция имеет первообразную на промежуткеX. Интегрируя последнее равенство, получаем формулу интегрирования по частям.

Замечание. Так как , то формулу интегрирования по частям в неопределенном интеграле можно записать в виде

.

Пример

.

Замечание. Формула интегрирования по частям может применяться неоднократно.

Пример